【A典学案】冲刺100分 七年级上专题复习第六讲 数据的收集与整理(34张)
文档属性
| 名称 | 【A典学案】冲刺100分 七年级上专题复习第六讲 数据的收集与整理(34张) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览










文档简介
第六讲 数据的收集与整理
北师大版 七年级上册
知识清单
1.数据的收集
(1)调查可分为全面调查(普查)和抽样___________.
(2)我们把 _____________________ 叫做总体, _______________________ 叫做个体, ______________________________ 叫做总体的一个样本, _______
________________ 叫做样本容量.
2.数据的表示
(1)数据整理的方式有统计表与 ___________ .
(2)统计图包括条形统计图、 ____________ 和 ______________
调查
所有考察对象的全体
其中每一个考察对象
从总体中所抽取的一部分个体
样本中
个体的数目
统计图
折线统计图
扇形统计图
知识清单
3.扇形统计图
利用圆和扇形来表示总体和部分的关系,即用圆代表 ______ ,圆中的各个扇形分别代表 _______________________ ,扇形的大小反映部分占总体的
__________ 的大小.
4.制作扇形统计图的方法
(1)计算各部分占总体的 __________ ;(2)计算各部分对应的扇形的 ______________ ;(3)画出扇形统计图,标上 ________
总体
总体中的不同部分
百分比
百分比
圆心角的度数
百分比
知识清单
5.频数直方图
(1)频数直方图是一种特殊的条形统计图,它将统计对象的数据进行了分组,画在数轴上,纵轴表示各组数据的频数.
(2)如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
(3)画频数直方图的步骤:①找出所有数据中的最大值和最小值,确定统计量的范围;②确定组数和组距并进行分组,数据个数在100以内,一般分5至12组;③统计每组中数据的频数;④根据分组和频数,绘制频数直方图
知识清单
6.三种统计图的特点
(1)条形统计图:能清楚地表示出各部分的具体数目;
(2)折线统计图:能清楚地反映事物的变化情况;
(3)扇形统计图:能清楚地表示出各部分在总体中所占的百分比.
典例精讲
类型之一 选择合适的调查方式
【例1】下列调查中,适合用全面调查的是( )
A.了解某班学生50米跑的乘积 B.了解一批灯泡的使用寿命
C.了解一批炮弹的杀伤半径 D.了解一批袋装食品是否含有防腐剂
[解析]本题考查了数据的收集与整理及其相关概念的知识.全面调查是对所考察的对象逐一进行调查,而抽样调查则是从总体中抽取部分个体进行的部分调查.A选项某班学生人数比较少,可采用全面调查,而B,C,D选项若采用全面调查,会造成破坏性.故选A
变式训练
1.以下问题,不适合用全面调查的是( )
A.旅客上飞机前的安检 B.学校招聘教师,对应聘人员的面试
C.了解全校学生的课外读书时间 D.了解一批灯泡的使用寿命
【答案】D
典例精讲
类型之二 总体、个体和样本
【例2】为了了解某校七年级1000名学生的体重情况,从中抽查100名学生体重进行统计分析,在这个问题中,样本是指( )
A.1000名学生 B.被抽取的100名学生
C.1000名学生的体重 D.被抽取得到100名学生的体重
[解析]样本是指从中抽取到的100名学生的体重.
故选D.
变式训练
2.某市有3万名学生参加2020年的中考,想要了解这3万名学生的数学成绩,从中抽取了500名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本 B.每个考生的数学成绩是个体
C.3万名考生是总体 D.以上说法均不对
【答案】3万名考生的数学成绩是总体,所以C项不正确;500名考生的数学成绩是总体的一个样本,所以A项也不正确;每个考生的数学成绩是个体,故B项正确,D项不正确.故选B.
典例精讲
类型之三 根据统计图获取信息
【例3】学生的学习兴趣如何是每位教师非常关注的问题.为此某校教师对该校部分学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣),并将调查结果绘制成如图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
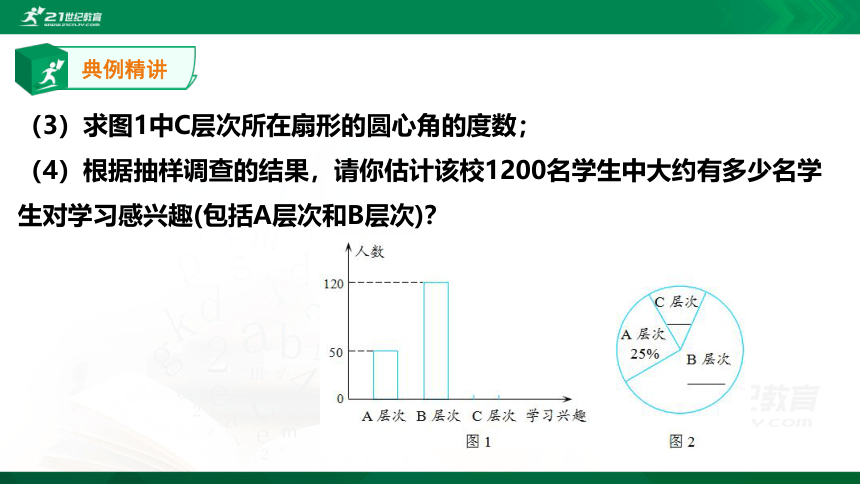
(1)此次抽样调查中,共调查了_______名学生;
(2)将图1、图2补充完整;
典例精讲
(3)求图1中C层次所在扇形的圆心角的度数;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣(包括A层次和B层次)?
典例精讲
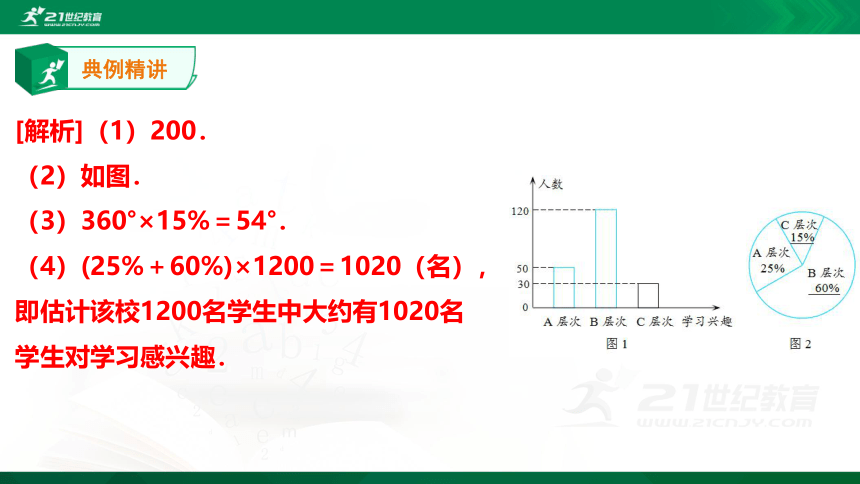
[解析](1)200.
(2)如图.
(3)360°×15%=54°.
(4)(25%+60%)×1200=1020(名),
即估计该校1200名学生中大约有1020名
学生对学习感兴趣.
变式训练
3.某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.
如图1,2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:
(1)此次调查的人数为________人;
(2)条形统计图中存在的错误是________(填A,B,C,D中的一个),并
变式训练
在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
【答案】(1)200.
(2)C;C等级的人数应为50,图略.(3)D等级的人数为30,图略.
(4)600×(20%+40%)=360(人).
答:该校对此活动“非常喜欢”和“比较喜欢”的学生共有360人.
典例精讲
类型之四 制作统计图
【例4】小明班上的同学在一次课外活动中,有8人打乒乓球,12人打排球,10人打篮球,6人打羽毛球,剩下的4人当裁判.请你制作扇形统计图表示参加各项活动人数占总人数的百分比.
【答案】(1)计算各部分占总体的百分比,即百分比=(各部分频数÷总频数)×100%.
本题中,全班总人数为8+12+10+6+4=40(人),
打乒乓球的占总体的百分比为(8÷40)×100%=20%,
典例精讲
打排球的占总体的百分比为(12÷40)×100%=30%,
打篮球的占总体的百分比为(10÷40)×100%=25%,
打羽毛球的占总体的百分比为(6÷40)×100%=15%,
当裁判的占总体的百分比为(4÷40)×100%=10%.
(2)计算各部分相应的扇形圆心角的度数,即圆心角的度数=百分比×360°.本题中,相应扇形的圆心角依次为
20%×360°=72°,30%×360°=108°,25%×360°=90°,15%×360°=54°,10%×360°=36°.
典例精讲
(3)如图,用圆规画圆,再利用量角器作出各圆心角,从而把圆面分成若干个扇形.
(4)将各部分的标题及所占总体的百分比标注在相应的扇形上.
变式训练
4.已知一个样本数据:
25 21 23 25 27 29 25 28 30 29
26 24 25 27 26 22 24 25 26 28
(1)制作频数分布表;
(2)绘制频数直方图.
变式训练
【答案】(1)频数分布表,如下表:
(2)频数直方图如下:
区校真题
1.(罗湖)下列调查中,①检测朝阳市的空气质量;②为了解某中东呼吸综合征(MERS)确诊病人同一架飞机乘客的健康情况;③为保证“神舟9号”成功发射,对其零部件进行检测;④调查某班50名同学的视力情况.其中适合采用抽样调查的是( )
A.① B.②
C.③ D.④
A
区校真题
2.(深高)为了调查某校学生的视力情况,在全校的800名学生中随机抽取了80名学生,下列说法正确的是( )
A.此次调查属于全面调查 B.样本容量是80
C.800名学生是总体 D.被抽取的每一名学生称为个体
B
区校真题
3.(龙华)金庸先生笔下的“五岳剑派”就是在以下五大名山中:
若想根据表中数据绘制统计图,以便更清楚的比较这五座山的高度,最合适的是( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都可以
C
区校真题
4.(南山)我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》,通知中要求各学校全面持续开展“光盘行动”.深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度(程度分为:“A:了解很多”,“B:了解较多”,“C:了解较少”,“D:不了解”),对本市某所中学的学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅不完整统计图:
根据以上信息,解答下列问题:
(1)补全条形统计图;
区校真题
(2)本次抽样调查了_______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
(3)若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
区校真题
【解答】(1)∵被调查的学生总人数为30÷30%=100(人),
则C对应的人数为100-(30+45+5)=20(人),
补全图形如图.
(2)由(1)知本次抽样调查了100名学生,
则扇形统计图中,“D”的部分所对应的圆心角度数为
360°× =18°,故答案为:100;
(3)估计这所中学的所有学生中,
对“节约教育”内容“了解较少”的有2000× =400(名).
区校真题
5.(龙华)某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成绩x均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图.
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为__________人;
(2)成绩为60≤x<70这一组的人数占整体人数的百分比为______;
(3)成绩为70≤x<80这一组的所在的扇形的圆心角度数为______;
区校真题
(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有______人.
区校真题
【解答】解:(1)所抽取分析的学生数量为8÷20%=40(人),故答案为:40.
(2)成绩为60≤x<70这一组的人数占体人数的百分比为 ×100%=15%,故答案为:15%.
(3)成绩为70≤x<80这一组的所在的扇形的圆心角度数为360°×20%=72°,故答案为:72°.
(4)成绩为90≤x<100的人数为40× =12(人),
则成绩为80≤x<90的人数为40-(6+8+12)=14(人).
区校真题
补全频数分布直方图如下:
(5)参加这次比赛的学生中属于“优秀”等级的
约有400× =120(人),
故答案为:120.
中考链接
某校有学生3000人,现欲开展学校社团活动,准备组建摄影社、国学社、篮球社、科技制作社四个社团.每名学生最多只能报一个社团,也可以不报.为了估计各社团人数,现在学校随机抽取了50名学生做问卷调查,得到了如图所示的两个不完全统计图.
结合以上信息,回答下列问题:
(1)本次抽样调查的样本容量是_______;
(2)请你补全条形统计图,并在图上标明具体数据;
(3)求参与科技制作社团所在扇形的圆心角度数;
中考链接
(4)请你估计全校有多少学生报名参加篮球社团活动.
中考链接
【答案】解:(1)本次抽样调查的样本容量是 =50,
故答案为:50;
(2)参与篮球社的人数=50×20%=10人,
参与国学社的人数为50-5-10-12-8=15人,
补全条形统计图如图所示;
(3)参与科技制作社团所在扇形的圆心角度数为360°× =86.4°;
(4)3000×20%=600名,
答:全校有600名学生报名参加篮球社团活动.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版 七年级上册
知识清单
1.数据的收集
(1)调查可分为全面调查(普查)和抽样___________.
(2)我们把 _____________________ 叫做总体, _______________________ 叫做个体, ______________________________ 叫做总体的一个样本, _______
________________ 叫做样本容量.
2.数据的表示
(1)数据整理的方式有统计表与 ___________ .
(2)统计图包括条形统计图、 ____________ 和 ______________
调查
所有考察对象的全体
其中每一个考察对象
从总体中所抽取的一部分个体
样本中
个体的数目
统计图
折线统计图
扇形统计图
知识清单
3.扇形统计图
利用圆和扇形来表示总体和部分的关系,即用圆代表 ______ ,圆中的各个扇形分别代表 _______________________ ,扇形的大小反映部分占总体的
__________ 的大小.
4.制作扇形统计图的方法
(1)计算各部分占总体的 __________ ;(2)计算各部分对应的扇形的 ______________ ;(3)画出扇形统计图,标上 ________
总体
总体中的不同部分
百分比
百分比
圆心角的度数
百分比
知识清单
5.频数直方图
(1)频数直方图是一种特殊的条形统计图,它将统计对象的数据进行了分组,画在数轴上,纵轴表示各组数据的频数.
(2)如果样本中数据较多,数据的差距也比较大时,频数直方图能更清晰、更直观地反映数据的整体状况.
(3)画频数直方图的步骤:①找出所有数据中的最大值和最小值,确定统计量的范围;②确定组数和组距并进行分组,数据个数在100以内,一般分5至12组;③统计每组中数据的频数;④根据分组和频数,绘制频数直方图
知识清单
6.三种统计图的特点
(1)条形统计图:能清楚地表示出各部分的具体数目;
(2)折线统计图:能清楚地反映事物的变化情况;
(3)扇形统计图:能清楚地表示出各部分在总体中所占的百分比.
典例精讲
类型之一 选择合适的调查方式
【例1】下列调查中,适合用全面调查的是( )
A.了解某班学生50米跑的乘积 B.了解一批灯泡的使用寿命
C.了解一批炮弹的杀伤半径 D.了解一批袋装食品是否含有防腐剂
[解析]本题考查了数据的收集与整理及其相关概念的知识.全面调查是对所考察的对象逐一进行调查,而抽样调查则是从总体中抽取部分个体进行的部分调查.A选项某班学生人数比较少,可采用全面调查,而B,C,D选项若采用全面调查,会造成破坏性.故选A
变式训练
1.以下问题,不适合用全面调查的是( )
A.旅客上飞机前的安检 B.学校招聘教师,对应聘人员的面试
C.了解全校学生的课外读书时间 D.了解一批灯泡的使用寿命
【答案】D
典例精讲
类型之二 总体、个体和样本
【例2】为了了解某校七年级1000名学生的体重情况,从中抽查100名学生体重进行统计分析,在这个问题中,样本是指( )
A.1000名学生 B.被抽取的100名学生
C.1000名学生的体重 D.被抽取得到100名学生的体重
[解析]样本是指从中抽取到的100名学生的体重.
故选D.
变式训练
2.某市有3万名学生参加2020年的中考,想要了解这3万名学生的数学成绩,从中抽取了500名考生的数学成绩进行统计分析,以下说法正确的是( )
A.这500名考生是总体的一个样本 B.每个考生的数学成绩是个体
C.3万名考生是总体 D.以上说法均不对
【答案】3万名考生的数学成绩是总体,所以C项不正确;500名考生的数学成绩是总体的一个样本,所以A项也不正确;每个考生的数学成绩是个体,故B项正确,D项不正确.故选B.
典例精讲
类型之三 根据统计图获取信息
【例3】学生的学习兴趣如何是每位教师非常关注的问题.为此某校教师对该校部分学生的学习兴趣进行了一次抽样调查(把学生的学习兴趣分为三个层次,A层次:很感兴趣;B层次:较感兴趣;C层次:不感兴趣),并将调查结果绘制成如图①和图②的统计图(不完整).请你根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了_______名学生;
(2)将图1、图2补充完整;
典例精讲
(3)求图1中C层次所在扇形的圆心角的度数;
(4)根据抽样调查的结果,请你估计该校1200名学生中大约有多少名学生对学习感兴趣(包括A层次和B层次)?
典例精讲
[解析](1)200.
(2)如图.
(3)360°×15%=54°.
(4)(25%+60%)×1200=1020(名),
即估计该校1200名学生中大约有1020名
学生对学习感兴趣.
变式训练
3.某校课外小组为了解同学们对学校“阳光跑操”活动的喜欢程度,抽取部分学生进行调查.被调查的每个学生按A(非常喜欢)、B(比较喜欢)、C(一般)、D(不喜欢)四个等级对活动评价.
如图1,2是该小组采集数据后绘制的两幅统计图.经确认扇形统计图是正确的,而条形统计图尚有一处错误且并不完整.请你根据统计图提供的信息,解答下列问题:
(1)此次调查的人数为________人;
(2)条形统计图中存在的错误是________(填A,B,C,D中的一个),并
变式训练
在图中加以改正;
(3)在图2中补画条形统计图中不完整的部分;
(4)如果该校有600名学生,那么对此活动“非常喜欢”和“比较喜欢”的学生共有多少人?
【答案】(1)200.
(2)C;C等级的人数应为50,图略.(3)D等级的人数为30,图略.
(4)600×(20%+40%)=360(人).
答:该校对此活动“非常喜欢”和“比较喜欢”的学生共有360人.
典例精讲
类型之四 制作统计图
【例4】小明班上的同学在一次课外活动中,有8人打乒乓球,12人打排球,10人打篮球,6人打羽毛球,剩下的4人当裁判.请你制作扇形统计图表示参加各项活动人数占总人数的百分比.
【答案】(1)计算各部分占总体的百分比,即百分比=(各部分频数÷总频数)×100%.
本题中,全班总人数为8+12+10+6+4=40(人),
打乒乓球的占总体的百分比为(8÷40)×100%=20%,
典例精讲
打排球的占总体的百分比为(12÷40)×100%=30%,
打篮球的占总体的百分比为(10÷40)×100%=25%,
打羽毛球的占总体的百分比为(6÷40)×100%=15%,
当裁判的占总体的百分比为(4÷40)×100%=10%.
(2)计算各部分相应的扇形圆心角的度数,即圆心角的度数=百分比×360°.本题中,相应扇形的圆心角依次为
20%×360°=72°,30%×360°=108°,25%×360°=90°,15%×360°=54°,10%×360°=36°.
典例精讲
(3)如图,用圆规画圆,再利用量角器作出各圆心角,从而把圆面分成若干个扇形.
(4)将各部分的标题及所占总体的百分比标注在相应的扇形上.
变式训练
4.已知一个样本数据:
25 21 23 25 27 29 25 28 30 29
26 24 25 27 26 22 24 25 26 28
(1)制作频数分布表;
(2)绘制频数直方图.
变式训练
【答案】(1)频数分布表,如下表:
(2)频数直方图如下:
区校真题
1.(罗湖)下列调查中,①检测朝阳市的空气质量;②为了解某中东呼吸综合征(MERS)确诊病人同一架飞机乘客的健康情况;③为保证“神舟9号”成功发射,对其零部件进行检测;④调查某班50名同学的视力情况.其中适合采用抽样调查的是( )
A.① B.②
C.③ D.④
A
区校真题
2.(深高)为了调查某校学生的视力情况,在全校的800名学生中随机抽取了80名学生,下列说法正确的是( )
A.此次调查属于全面调查 B.样本容量是80
C.800名学生是总体 D.被抽取的每一名学生称为个体
B
区校真题
3.(龙华)金庸先生笔下的“五岳剑派”就是在以下五大名山中:
若想根据表中数据绘制统计图,以便更清楚的比较这五座山的高度,最合适的是( )
A.扇形统计图 B.折线统计图
C.条形统计图 D.以上都可以
C
区校真题
4.(南山)我省教育厅下发了《在全省中小学幼儿园广泛开展节约教育的通知》,通知中要求各学校全面持续开展“光盘行动”.深圳市教育局督导组为了调查学生对“节约教育”内容的了解程度(程度分为:“A:了解很多”,“B:了解较多”,“C:了解较少”,“D:不了解”),对本市某所中学的学生进行了抽样调查.我们将这次调查的结果绘制了以下两幅不完整统计图:
根据以上信息,解答下列问题:
(1)补全条形统计图;
区校真题
(2)本次抽样调查了_______名学生;在扇形统计图中,求出“D”的部分所对应的圆心角度数.
(3)若该中学共有2000名学生,请你估计这所中学的所有学生中,对“节约教育”内容“了解较少”的有多少人.
区校真题
【解答】(1)∵被调查的学生总人数为30÷30%=100(人),
则C对应的人数为100-(30+45+5)=20(人),
补全图形如图.
(2)由(1)知本次抽样调查了100名学生,
则扇形统计图中,“D”的部分所对应的圆心角度数为
360°× =18°,故答案为:100;
(3)估计这所中学的所有学生中,
对“节约教育”内容“了解较少”的有2000× =400(名).
区校真题
5.(龙华)某学校组织七年级学生参加了一次“运算能力”比赛,共有400名学生参加,参赛学生的成绩x均为正数,且最低分为60分,为了解本次比赛学生的成绩分布情况,抽取了其中部分学生的成绩作为样本进行统计,并制作出了如下两个统计图.
请根据所给信息,解答下列问题:
(1)所抽取分析的学生数量为__________人;
(2)成绩为60≤x<70这一组的人数占整体人数的百分比为______;
(3)成绩为70≤x<80这一组的所在的扇形的圆心角度数为______;
区校真题
(4)请补全频数分布直方图;
(5)若成绩达到90分或以上为“优秀”等级,则参加这次比赛的学生中属于“优秀”等级的约有______人.
区校真题
【解答】解:(1)所抽取分析的学生数量为8÷20%=40(人),故答案为:40.
(2)成绩为60≤x<70这一组的人数占体人数的百分比为 ×100%=15%,故答案为:15%.
(3)成绩为70≤x<80这一组的所在的扇形的圆心角度数为360°×20%=72°,故答案为:72°.
(4)成绩为90≤x<100的人数为40× =12(人),
则成绩为80≤x<90的人数为40-(6+8+12)=14(人).
区校真题
补全频数分布直方图如下:
(5)参加这次比赛的学生中属于“优秀”等级的
约有400× =120(人),
故答案为:120.
中考链接
某校有学生3000人,现欲开展学校社团活动,准备组建摄影社、国学社、篮球社、科技制作社四个社团.每名学生最多只能报一个社团,也可以不报.为了估计各社团人数,现在学校随机抽取了50名学生做问卷调查,得到了如图所示的两个不完全统计图.
结合以上信息,回答下列问题:
(1)本次抽样调查的样本容量是_______;
(2)请你补全条形统计图,并在图上标明具体数据;
(3)求参与科技制作社团所在扇形的圆心角度数;
中考链接
(4)请你估计全校有多少学生报名参加篮球社团活动.
中考链接
【答案】解:(1)本次抽样调查的样本容量是 =50,
故答案为:50;
(2)参与篮球社的人数=50×20%=10人,
参与国学社的人数为50-5-10-12-8=15人,
补全条形统计图如图所示;
(3)参与科技制作社团所在扇形的圆心角度数为360°× =86.4°;
(4)3000×20%=600名,
答:全校有600名学生报名参加篮球社团活动.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
