等腰三角形的轴对称性(2)

1.5等腰三角形的轴对称性（2）
姓名_________ 班级 ________ 学号 等第
学习目标
掌握“等角对等边”的性质
掌握“直角三角形斜边上的中线等于斜边的一半”的性质
经历“折纸、画图、观察、归纳”的活动过程，发展学生的空间观念和抽象概括能力，感受分类、转化等数学思想方法；
会用“因为……所以……理由是……”等方式来进行说理，进一步发展有条理的思考和表达，提高演绎推理的能力
学习重点
熟练的掌握“等角对等边”及直角三角的重要性质
学习难点
正确熟练的运用解决问题
学习过程
1.探索发现
（1）.将一张长方形的纸条上任意画出一条截线AB，所得的∠1与∠2相等吗？为什么？
经过折叠后所得的△ABC，在所得的三角形中∠1=∠2。那么请同学们度量边AC，BC的长度，你们有什么发现？
（2）.在一张薄纸上画线段AB，并在AB同侧利用量角器画两个相等的锐角∠BAM和∠ABM.设AM与BN相交于点C.量一量AC与BC的长度，AC和BC相等吗？你和同学所得的结论相同吗？
2.例题分析
例1. 如图，在△ABC中，AB = AC，两条角平分线BD、CE相交于点O。
(1).OB与OC相等吗？请说明理由。
⑵.BD与CE相等吗 为什么
⑶.如果将BD与CE变为高或中线，⑵中的结论还成立吗 为什么
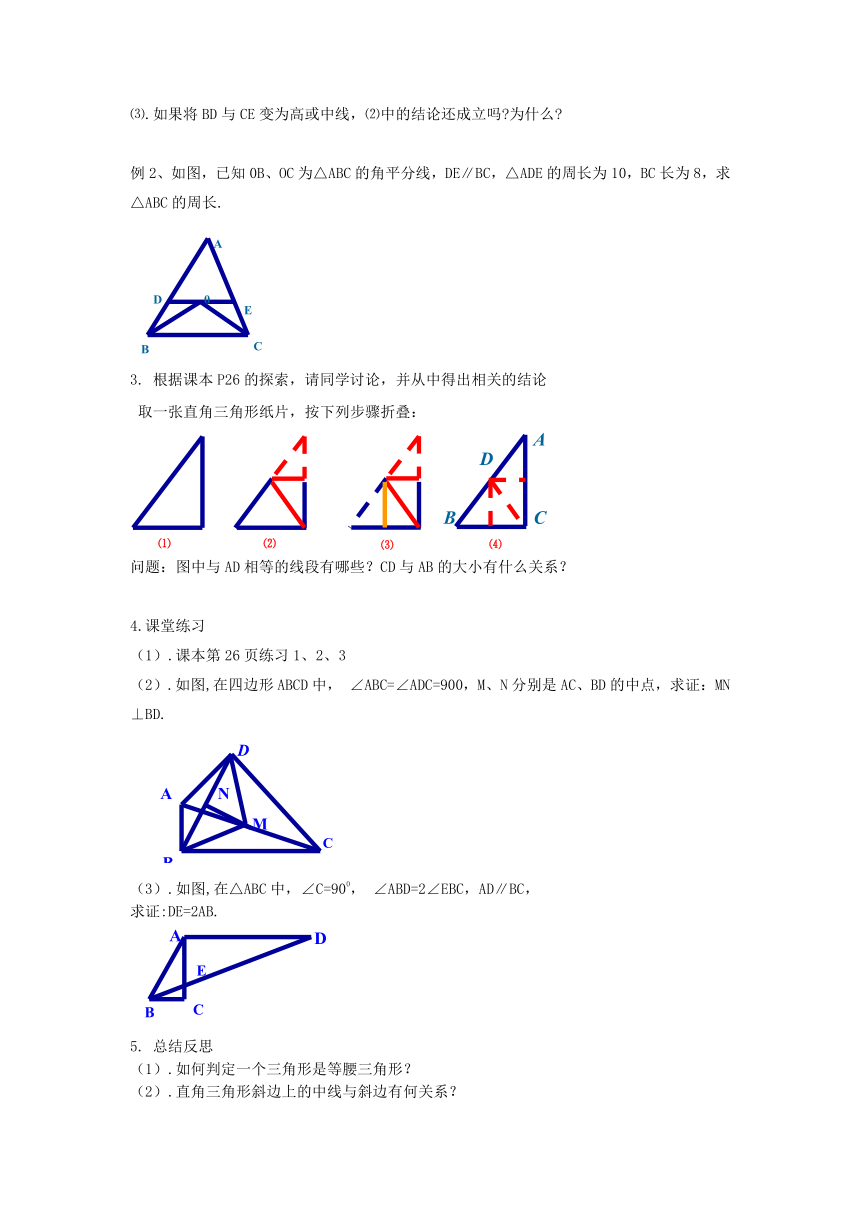
例2、如图，已知0B、OC为△ABC的角平分线，DE∥BC，△ADE的周长为10，BC长为8，求△ABC的周长.
3. 根据课本P26的探索，请同学讨论，并从中得出相关的结论
取一张直角三角形纸片，按下列步骤折叠：
问题：图中与AD相等的线段有哪些？CD与AB的大小有什么关系？
4.课堂练习
（1）.课本第26页练习1、2、3
（2）.如图,在四边形ABCD中， ∠ABC=∠ADC=900，M、N分别是AC、BD的中点，求证：MN⊥BD.
（3）.如图,在△ABC中，∠C=900， ∠ABD=2∠EBC，AD∥BC，
求证:DE=2AB.
5. 总结反思
（1）.如何判定一个三角形是等腰三角形？
（2）.直角三角形斜边上的中线与斜边有何关系？
作业设计
班级 姓名 学号 等第
1．等腰三角形的识别：如果一个三角形有两个角 ，那么这两个角所对的边 .简称 ．
2．直角三角形 等于 的一半.
3．在△ABC中，∠A=30°，当∠B= 时，△ABC为等腰三角形；
当∠B= 时，△ABC为直角三角形．
4．如图，已知AC=CD=DA=CB=DE，则此图中共有 个等腰三角形，有 个直角三角形，AC= = .
5．在△ABC中，∠C=90°，D是AB的中点，若AB=18㎝，
则CD= .
6．如图，BC=BD，∠C=∠D，你能判断AC与AD的长度有什么关系吗？请说明理由．
7.在△ABC中，已知点E在BA的延长线上，并且∠1=∠2，AD∥BC．
问：△ABC是什么三角形？为什么？
8．如图，△ABC中，BE、CF分别是AC、AB边上的高，D是BC边上的中点，试说明DE=DF.
9.在△ABC中，∠ABC、∠ACB的平分线相交于点O，过点O作DE∥BC，分别交AB、AC于点D、E.请说明DE=BD+EC.
选做习题
10．如图，已知△ABC中，∠B=90°,AB=BC,BD=CE,M是AC边上的中点，求证：△DEM是等腰三角形．
11.如图在△ABC中，M,N分别是BC与EF的中点，CF⊥AB，BE⊥AC，证明：MN ⊥EF.
A
B
C
D
E
0
A
B
C
D
⑴
⑵
⑶
⑷
A
C
B
D
M
N
A
B
C
D
E
A
B
C
D
E
A
B
C
D
E
0
A
B
C
F
E
N
M