2020-2021学年湘教新版八年级上册数学期末复习试卷(Word版 含解析)
文档属性
| 名称 | 2020-2021学年湘教新版八年级上册数学期末复习试卷(Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 346.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览



文档简介
2020-2021学年湘教新版八年级上册数学期末复习试卷
一.选择题(共10小题,满分40分,每小题4分)
1.分式有意义的条件是( )
A.x≠0
B.y≠0
C.x≠3
D.x≠﹣3
2.下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
3.的算术平方根为( )
A.9
B.±9
C.3
D.±3
4.关于x的不等式(m+1)x>m+1的解集为x<1,那么m的取值范围是( )
A.m<﹣1
B.m>﹣1
C.m>0
D.m<0
5.三角形的外角和等于( )
A.90°
B.180°
C.360°
D.540°
6.世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )
A.5.6×10﹣1
B.5.6×10﹣2
C.5.6×10﹣3
D.0.56×10﹣1
7.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为( )
A.30°
B.15°
C.25°
D.20°
8.已知实数x,y满足,则y的值是( )
A.2
B.﹣2
C.0
D.3
9.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5°
B.8°
C.10°
D.15°
10.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
二.填空题(共8小题,满分32分,每小题4分)
11.使等式(2x+3)x+2020=1成立的x的值为
.
12.在实数范围内分解因式:m4﹣2m2=
.
13.命题“对顶角相等”的逆命题是
.
14.如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为
.
15.已知△ABC三边长分别为3,5,7,△DEF三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为
.
16.在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则2个空格的实数之积为
.
3
2
1
6
3
17.若关于x的不等式2x﹣a≤0的正整数解是1、2、3,则a的取值范围是
.
18.如图所示,将形状大小完全相同的“?”按照一定规律摆成下列图形,第1幅图中“?”的个数为a1,第2幅图中“?”的个数为a2,第3幅图中“?”的个数为a3,…,以此类推,若+++…+=.(n为正整数),则n的值为
.
三.解答题(共7小题,满分78分)
19.(10分)计算:
(1)÷﹣×+;
(2)解方程:﹣=1.
20.(10分)解不等式组把它的解集在数轴上表示出来,并写出不等式组的非负整数解.
21.(10分)已知:a2﹣a﹣2=0,求代数式的值.
22.(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有
个,以点O为交点的“8字型”有
个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
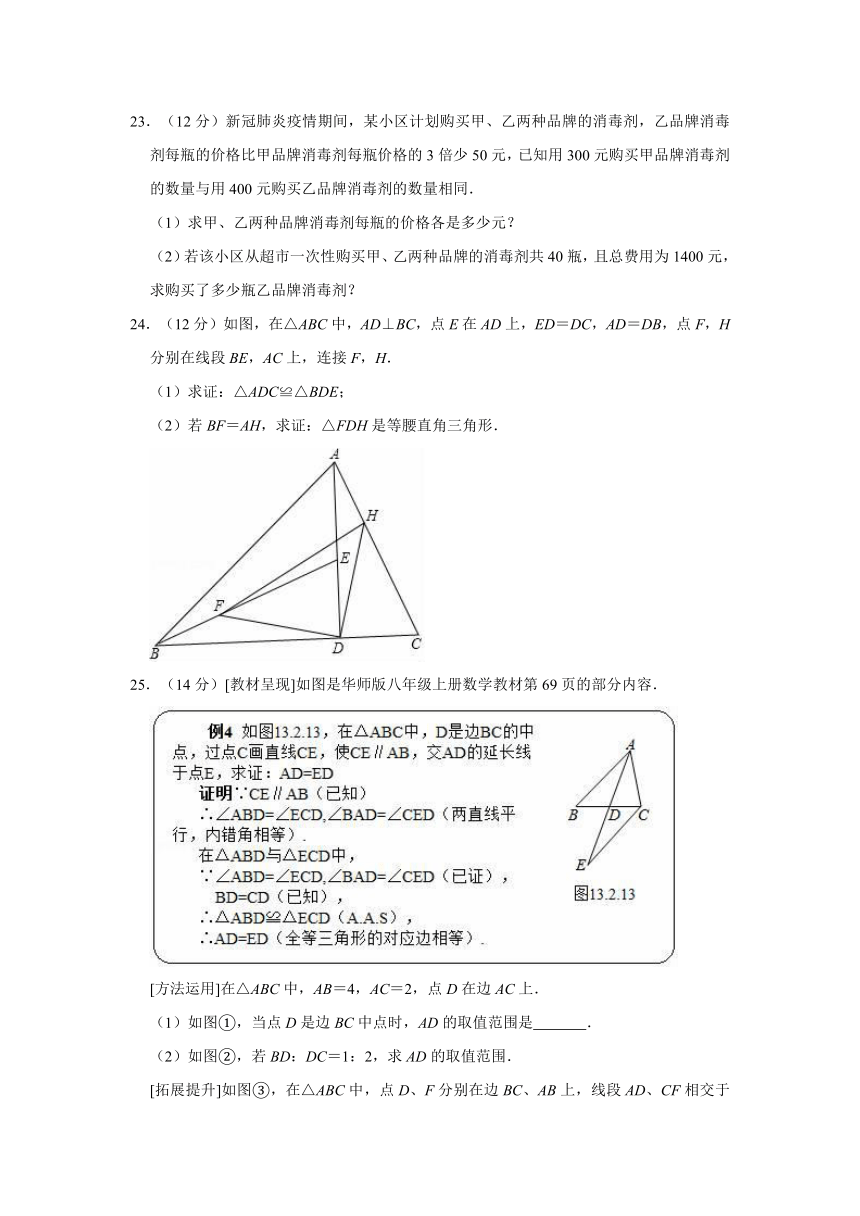
23.(12分)新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
24.(12分)如图,在△ABC中,AD⊥BC,点E在AD上,ED=DC,AD=DB,点F,H分别在线段BE,AC上,连接F,H.
(1)求证:△ADC≌△BDE;
(2)若BF=AH,求证:△FDH是等腰直角三角形.
25.(14分)[教材呈现]如图是华师版八年级上册数学教材第69页的部分内容.
[方法运用]在△ABC中,AB=4,AC=2,点D在边AC上.
(1)如图①,当点D是边BC中点时,AD的取值范围是
.
(2)如图②,若BD:DC=1:2,求AD的取值范围.
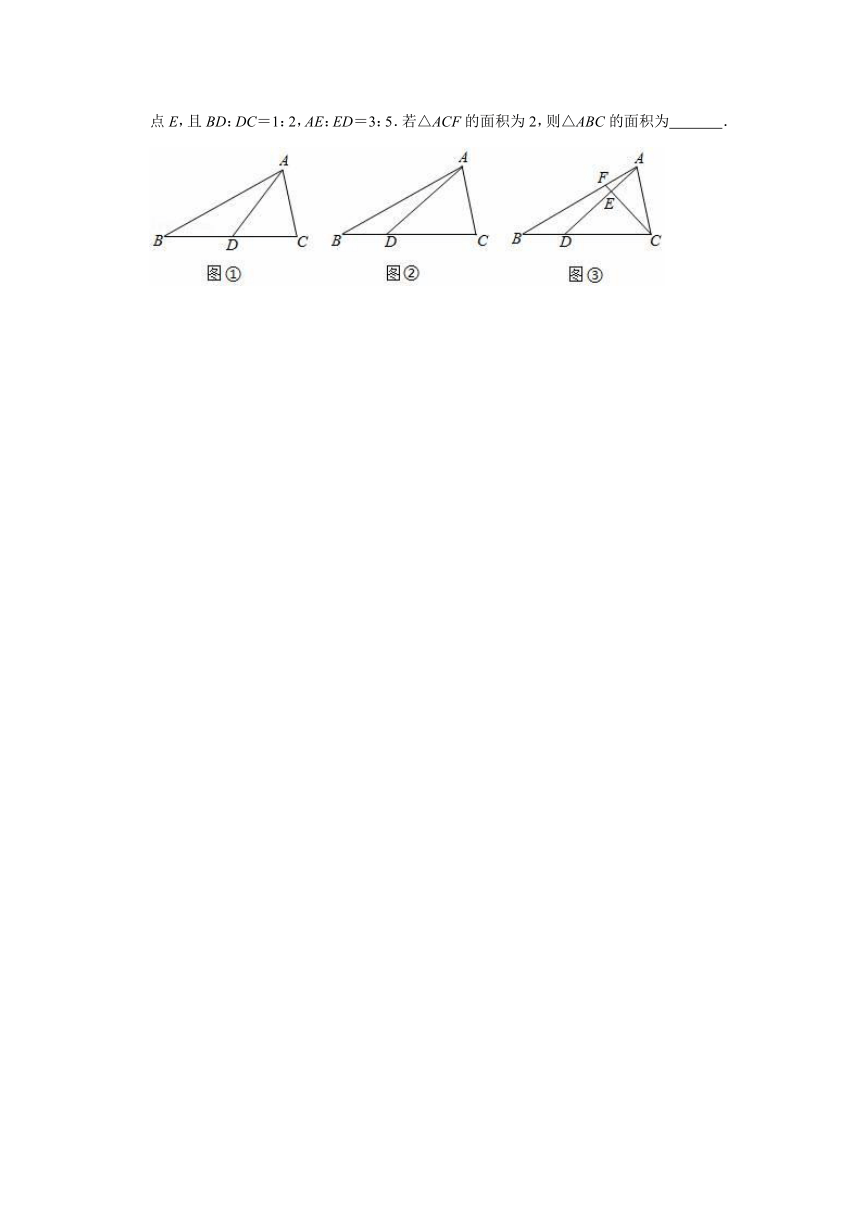
[拓展提升]如图③,在△ABC中,点D、F分别在边BC、AB上,线段AD、CF相交于点E,且BD:DC=1:2,AE:ED=3:5.若△ACF的面积为2,则△ABC的面积为
.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:根据分式有意义的条件,得x﹣3≠0
解得x≠3.
故选:C.
2.解:无理数有:0.101001…(相邻两个1之间的0的个数逐次加1),,,共3个,
故选:C.
3.解:∵=9,32=9
∴的算术平方根为3.
故选:C.
4.解:∵不等式(m+1)x>m+1的解集为x<1,
∴m+1<0,即m<﹣1,
故选:A.
5.解:三角形的外角和为360°,
故选:C.
6.解:将0.056用科学记数法表示为5.6×10﹣2,
故选:B.
7.解:∵AD⊥BC,
∴∠BDF=∠ADC,
又∵∠BFD=∠AFE,
∴∠CAD=∠FBD,
在△BDF和△ADC中
,
∴△BDF≌△ADC
(AAS)
∴∠DBF=∠CAD=25°,
∵DB=DA,∠ADB=90°,
∴∠ABD=45°,
∴∠ABE=∠ABD﹣∠DBF=20°
故选:D.
8.解:由题意可知:x+2=0,3x+y+8=0,
∴x=﹣2,y=﹣2,
故选:B.
9.解:∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=∠BCA=×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选:C.
10.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选:D.
二.填空题(共8小题,满分32分,每小题4分)
11.解:当x+2020=0时,
∴x=﹣2020,
∴2x+3=﹣4037≠0,符合题意,
当2x+3=1时,
∴x=﹣1,符合题意,
当2x+3=﹣1时,
∴x=﹣2,
∴x+2020=2018,符合题意,
故答案为:x=﹣2或x=﹣1或x=﹣2020.
12.解:m4﹣2m2
=m2(m2﹣2)
=m2(m+)(m﹣).
故答案为:m2(m+)(m﹣).
13.解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为:相等的角为对顶角.
14.解:当△ACP≌△BPQ,
∴AP=BQ,
∵运动时间相同,
∴P,Q的运动速度也相同,
∴x=2.
当△ACP≌△BQP时,
AC=BQ=4,PA=PB,
∴t=1.5,
∴x==
故答案为2或.
15.解:∵△ABC三边长分别为3,5,7,△DEF三边长分别为3,3x﹣2,2x﹣1,这两个三角形全等,
∴3+5+7=3+3x﹣2+2x﹣1,
解得:x=3.
故答案为:3.
16.解:由题意可得:
xy=,
xy=.
故答案为:.
17.解:解不等式2x﹣a≤0,得:x≤,
∵其正整数解是1、2、3,
所以3≤<4,
解得6≤a<8,
故答案为:6≤a<8
18.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+++…+=,
∴+++…+=,
∴2×(1﹣+﹣+﹣+……+﹣)=,
∴2×(1﹣)=,
1﹣=,
解得n=4039,
经检验:n=4039是分式方程的解,
故答案为:4039.
三.解答题(共7小题,满分78分)
19.解:(1)原式=﹣+2
=4﹣+2
=4+;
(2)去分母得(x+2)2﹣4=(x+2)(x﹣2),
解得x=﹣1,
检验:当x=﹣1时,(x+2)(x﹣2)≠0,
所以原方程的解为x=﹣1.
20.解:,
由①得:x≥﹣1,
由②得:x<3,
∴不等式组的解集为﹣1≤x<3,
在数轴上表示,如图所示,
则其非负整数解为0,1,2.
21.解:原式=(+)?
=?
=?
=a+1,
∵a2﹣a﹣2=0,
∴(a+1)(a﹣2)=0,
解得a=﹣1或a=2,
∵a+1≠0,即a≠﹣1,
∴a=2,
则原式=2+1=3.
22.(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,
∴3∠P=∠B+2∠C.
23.解:(1)设甲品牌消毒剂每瓶的价格为x元;乙品牌消毒剂每瓶的价格为(3x﹣50)元,
由题意得:=,
解得:x=30,
经检验,x=30是原方程的解且符合实际意义,
3x﹣5═40,
答:甲品牌消毒剂每瓶的价格为30元;乙品牌消毒剂每瓶的价格为40元;
(2)设购买甲种品牌的消毒剂y瓶,则购买乙种品牌的消毒剂(40﹣y)瓶,
由题意得:30y+40(40﹣y)=1400,
解得:y=20,
∴40﹣y=40﹣20=20,
答:购买了20瓶乙品牌消毒剂.
24.(1)证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°.
在△BDE与△ADC中,,
∴△BDE≌△ADC(SAS).
(2)证明:由(1)得△BDE≌△ADC,
∴∠FBD=∠HAD.
在△FBD与△HAD中,,
∴△FBD≌△HAD(SAS).
∴∠FDB=∠HDA,FD=HD.
∴∠FDB+∠FDE=∠HDA+∠FDE=90°,
∴∠FDH=90°,
∴△FDH是等腰直角三角形.
25.解:[方法运用]
(1)延长AD至点E,使得DE=AD,连接CE,
∵在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE,
∵△ACE中,CE﹣AC<AE<CE+AC,
∴2<AE<6,
∴1<AD<3.
故答案为:1<AD<3.
(2)如图2,过点C作CM∥AB,交AD的延长线于点M,
∴△ABD∽△MCD,
∴,
∵BD:DC=1:2,AB=4,
∴CM=8,AD=AM,
在△AMC中,
∵CM=8,AC=2,
∴6<AM<10,
∴2<AD<.
[拓展提升]解:如图3,过点A作AM∥BC交CF的延长线于点M,
∴△AME∽△DCE,
∴,
∵,
∴,
∴,
同理△AMF∽△BCF,
∴,
∴.
∴,
∵△ACF的面积为2,
∴△ABC的面积为7.
故答案为:7.
一.选择题(共10小题,满分40分,每小题4分)
1.分式有意义的条件是( )
A.x≠0
B.y≠0
C.x≠3
D.x≠﹣3
2.下列各数:0.101001…(相邻两个1之间的0的个数逐次加1),,,,,中,无理数有( )
A.1个
B.2个
C.3个
D.4个
3.的算术平方根为( )
A.9
B.±9
C.3
D.±3
4.关于x的不等式(m+1)x>m+1的解集为x<1,那么m的取值范围是( )
A.m<﹣1
B.m>﹣1
C.m>0
D.m<0
5.三角形的外角和等于( )
A.90°
B.180°
C.360°
D.540°
6.世界上最小的鸟是生活在古巴的吸蜜蜂鸟,它的质量约为0.056盎司.将0.056用科学记数法表示为( )
A.5.6×10﹣1
B.5.6×10﹣2
C.5.6×10﹣3
D.0.56×10﹣1
7.如图,在△ABC中,AD⊥BC于点D,BE⊥AC于点E,AD与BE相交于点F,若BF=AC,∠CAD=25°,则∠ABE的度数为( )
A.30°
B.15°
C.25°
D.20°
8.已知实数x,y满足,则y的值是( )
A.2
B.﹣2
C.0
D.3
9.如图,在△ABC中,∠B=50°,∠A=30°,CD平分∠ACB,CE⊥AB于点E,则∠DCE的度数是( )
A.5°
B.8°
C.10°
D.15°
10.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
二.填空题(共8小题,满分32分,每小题4分)
11.使等式(2x+3)x+2020=1成立的x的值为
.
12.在实数范围内分解因式:m4﹣2m2=
.
13.命题“对顶角相等”的逆命题是
.
14.如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为
.
15.已知△ABC三边长分别为3,5,7,△DEF三边长分别为3,3x﹣2,2x﹣1,若这两个三角形全等,则x为
.
16.在如图方格中,若要使横、竖、斜对角的3个实数相乘都得到同样的结果,则2个空格的实数之积为
.
3
2
1
6
3
17.若关于x的不等式2x﹣a≤0的正整数解是1、2、3,则a的取值范围是
.
18.如图所示,将形状大小完全相同的“?”按照一定规律摆成下列图形,第1幅图中“?”的个数为a1,第2幅图中“?”的个数为a2,第3幅图中“?”的个数为a3,…,以此类推,若+++…+=.(n为正整数),则n的值为
.
三.解答题(共7小题,满分78分)
19.(10分)计算:
(1)÷﹣×+;
(2)解方程:﹣=1.
20.(10分)解不等式组把它的解集在数轴上表示出来,并写出不等式组的非负整数解.
21.(10分)已知:a2﹣a﹣2=0,求代数式的值.
22.(10分)如图1,已知线段AB、CD相交于点O,连接AC、BD,则我们把形如这样的图形称为“8字型”.
(1)求证:∠A+∠C=∠B+∠D;
(2)如图2,若∠CAB和∠BDC的平分线AP和DP相交于点P,且与CD、AB分别相交于点M、N.
①以线段AC为边的“8字型”有
个,以点O为交点的“8字型”有
个;
②若∠B=100°,∠C=120°,求∠P的度数;
③若角平分线中角的关系改为“∠CAP=∠CAB,∠CDP=∠CDB”,试探究∠P与∠B、∠C之间存在的数量关系,并证明理由.
23.(12分)新冠肺炎疫情期间,某小区计划购买甲、乙两种品牌的消毒剂,乙品牌消毒剂每瓶的价格比甲品牌消毒剂每瓶价格的3倍少50元,已知用300元购买甲品牌消毒剂的数量与用400元购买乙品牌消毒剂的数量相同.
(1)求甲、乙两种品牌消毒剂每瓶的价格各是多少元?
(2)若该小区从超市一次性购买甲、乙两种品牌的消毒剂共40瓶,且总费用为1400元,求购买了多少瓶乙品牌消毒剂?
24.(12分)如图,在△ABC中,AD⊥BC,点E在AD上,ED=DC,AD=DB,点F,H分别在线段BE,AC上,连接F,H.
(1)求证:△ADC≌△BDE;
(2)若BF=AH,求证:△FDH是等腰直角三角形.
25.(14分)[教材呈现]如图是华师版八年级上册数学教材第69页的部分内容.
[方法运用]在△ABC中,AB=4,AC=2,点D在边AC上.
(1)如图①,当点D是边BC中点时,AD的取值范围是
.
(2)如图②,若BD:DC=1:2,求AD的取值范围.
[拓展提升]如图③,在△ABC中,点D、F分别在边BC、AB上,线段AD、CF相交于点E,且BD:DC=1:2,AE:ED=3:5.若△ACF的面积为2,则△ABC的面积为
.
参考答案与试题解析
一.选择题(共10小题,满分40分,每小题4分)
1.解:根据分式有意义的条件,得x﹣3≠0
解得x≠3.
故选:C.
2.解:无理数有:0.101001…(相邻两个1之间的0的个数逐次加1),,,共3个,
故选:C.
3.解:∵=9,32=9
∴的算术平方根为3.
故选:C.
4.解:∵不等式(m+1)x>m+1的解集为x<1,
∴m+1<0,即m<﹣1,
故选:A.
5.解:三角形的外角和为360°,
故选:C.
6.解:将0.056用科学记数法表示为5.6×10﹣2,
故选:B.
7.解:∵AD⊥BC,
∴∠BDF=∠ADC,
又∵∠BFD=∠AFE,
∴∠CAD=∠FBD,
在△BDF和△ADC中
,
∴△BDF≌△ADC
(AAS)
∴∠DBF=∠CAD=25°,
∵DB=DA,∠ADB=90°,
∴∠ABD=45°,
∴∠ABE=∠ABD﹣∠DBF=20°
故选:D.
8.解:由题意可知:x+2=0,3x+y+8=0,
∴x=﹣2,y=﹣2,
故选:B.
9.解:∵∠B=50°,CE⊥AB,
∴∠BCE=40°,
又∵∠A=30°,CD平分∠ACB,
∴∠BCD=∠BCA=×(180°﹣50°﹣30°)=50°,
∴∠DCE=∠BCD﹣∠BCE=50°﹣40°=10°,
故选:C.
10.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选:D.
二.填空题(共8小题,满分32分,每小题4分)
11.解:当x+2020=0时,
∴x=﹣2020,
∴2x+3=﹣4037≠0,符合题意,
当2x+3=1时,
∴x=﹣1,符合题意,
当2x+3=﹣1时,
∴x=﹣2,
∴x+2020=2018,符合题意,
故答案为:x=﹣2或x=﹣1或x=﹣2020.
12.解:m4﹣2m2
=m2(m2﹣2)
=m2(m+)(m﹣).
故答案为:m2(m+)(m﹣).
13.解:命题“对顶角相等”的逆命题是“相等的角为对顶角”.
故答案为:相等的角为对顶角.
14.解:当△ACP≌△BPQ,
∴AP=BQ,
∵运动时间相同,
∴P,Q的运动速度也相同,
∴x=2.
当△ACP≌△BQP时,
AC=BQ=4,PA=PB,
∴t=1.5,
∴x==
故答案为2或.
15.解:∵△ABC三边长分别为3,5,7,△DEF三边长分别为3,3x﹣2,2x﹣1,这两个三角形全等,
∴3+5+7=3+3x﹣2+2x﹣1,
解得:x=3.
故答案为:3.
16.解:由题意可得:
xy=,
xy=.
故答案为:.
17.解:解不等式2x﹣a≤0,得:x≤,
∵其正整数解是1、2、3,
所以3≤<4,
解得6≤a<8,
故答案为:6≤a<8
18.解:由图形知a1=1×2,a2=2×3,a3=3×4,
∴an=n(n+1),
∵+++…+=,
∴+++…+=,
∴2×(1﹣+﹣+﹣+……+﹣)=,
∴2×(1﹣)=,
1﹣=,
解得n=4039,
经检验:n=4039是分式方程的解,
故答案为:4039.
三.解答题(共7小题,满分78分)
19.解:(1)原式=﹣+2
=4﹣+2
=4+;
(2)去分母得(x+2)2﹣4=(x+2)(x﹣2),
解得x=﹣1,
检验:当x=﹣1时,(x+2)(x﹣2)≠0,
所以原方程的解为x=﹣1.
20.解:,
由①得:x≥﹣1,
由②得:x<3,
∴不等式组的解集为﹣1≤x<3,
在数轴上表示,如图所示,
则其非负整数解为0,1,2.
21.解:原式=(+)?
=?
=?
=a+1,
∵a2﹣a﹣2=0,
∴(a+1)(a﹣2)=0,
解得a=﹣1或a=2,
∵a+1≠0,即a≠﹣1,
∴a=2,
则原式=2+1=3.
22.(1)证明:在图1中,有∠A+∠C=180°﹣∠AOC,∠B+∠D=180°﹣∠BOD,
∵∠AOC=∠BOD,
∴∠A+∠C=∠B+∠D;
(2)解:①3;4;
故答案为:3,4;
②以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴2∠P+∠BAP+∠CDP=∠B+∠C+∠CAP+∠BDP,
∵AP、DP分别平分∠CAB和∠BDC,
∴∠BAP=∠CAP,∠CDP=∠BDP,
∴2∠P=∠B+∠C,
∵∠B=100°,∠C=120°,
∴∠P=(∠B+∠C)=(100°+120°)=110°;
③3∠P=∠B+2∠C,其理由是:
∵∠CAP=∠CAB,∠CDP=∠CDB,
∴∠BAP=∠CAB,∠BDP=∠CDB,
以M为交点“8字型”中,有∠P+∠CDP=∠C+∠CAP,
以N为交点“8字型”中,有∠P+∠BAP=∠B+∠BDP
∴∠C﹣∠P=∠CDP﹣∠CAP=(∠CDB﹣∠CAB),
∠P﹣∠B=∠BDP﹣∠BAP=(∠CDB﹣∠CAB).
∴2(∠C﹣∠P)=∠P﹣∠B,
∴3∠P=∠B+2∠C.
23.解:(1)设甲品牌消毒剂每瓶的价格为x元;乙品牌消毒剂每瓶的价格为(3x﹣50)元,
由题意得:=,
解得:x=30,
经检验,x=30是原方程的解且符合实际意义,
3x﹣5═40,
答:甲品牌消毒剂每瓶的价格为30元;乙品牌消毒剂每瓶的价格为40元;
(2)设购买甲种品牌的消毒剂y瓶,则购买乙种品牌的消毒剂(40﹣y)瓶,
由题意得:30y+40(40﹣y)=1400,
解得:y=20,
∴40﹣y=40﹣20=20,
答:购买了20瓶乙品牌消毒剂.
24.(1)证明:∵AD⊥BC,
∴∠BDE=∠ADC=90°.
在△BDE与△ADC中,,
∴△BDE≌△ADC(SAS).
(2)证明:由(1)得△BDE≌△ADC,
∴∠FBD=∠HAD.
在△FBD与△HAD中,,
∴△FBD≌△HAD(SAS).
∴∠FDB=∠HDA,FD=HD.
∴∠FDB+∠FDE=∠HDA+∠FDE=90°,
∴∠FDH=90°,
∴△FDH是等腰直角三角形.
25.解:[方法运用]
(1)延长AD至点E,使得DE=AD,连接CE,
∵在△ABD和△CDE中,
,
∴△ABD≌△CDE(SAS),
∴AB=CE,AD=DE,
∵△ACE中,CE﹣AC<AE<CE+AC,
∴2<AE<6,
∴1<AD<3.
故答案为:1<AD<3.
(2)如图2,过点C作CM∥AB,交AD的延长线于点M,
∴△ABD∽△MCD,
∴,
∵BD:DC=1:2,AB=4,
∴CM=8,AD=AM,
在△AMC中,
∵CM=8,AC=2,
∴6<AM<10,
∴2<AD<.
[拓展提升]解:如图3,过点A作AM∥BC交CF的延长线于点M,
∴△AME∽△DCE,
∴,
∵,
∴,
∴,
同理△AMF∽△BCF,
∴,
∴.
∴,
∵△ACF的面积为2,
∴△ABC的面积为7.
故答案为:7.
同课章节目录
