沪科版数学七年级下册第10章达标检测卷(含答案)
文档属性
| 名称 | 沪科版数学七年级下册第10章达标检测卷(含答案) |

|
|
| 格式 | rar | ||
| 文件大小 | 365.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-14 00:00:00 | ||
图片预览



文档简介
第10章达标检测卷
一、选择题(每题3分,共30分)
1.在下图中,∠1和∠2是对顶角的是( )
2.下面四种判定两条直线垂直的方法中,正确的有( )个.
①两条直线相交,有一个角是直角,则这两条直线互相垂直;②两条直线相交,有一组对顶角互补,则这两条直线互相垂直;③两条直线相交,四个角都相等,则这两条直线互相垂直;④两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
A.4 B.3 C.2 D.1
3.如图,在6×6的方格中,图①中的图形N平移后的位置如图②所示,则下列对图形N平移方法的叙述中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
4.直线a与直线b相交于点O,则直线b上到直线a的距离等于2 cm的点有( )
A.1个 B.2个 C.4个 D.无数个
5.如图,在江边有一个村庄赵庄,现要建一码头,为了使赵庄人乘船最方便,请你在岸上选一点来建码头,应建在( )
A.A点 B.B点 C.C点 D.D点
6.如图,AB∥CD,FE⊥DB,垂足为点E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
7.如图,若将木条a绕点O旋转后使其与木条b平行,则旋转的最小角度为( )
A.65° B.85° C.95° D.115°
8.已知:如图,点E,F分别在直线AB,CD上,点G,H在两直线之间,线段EF与GH相交于点O,且有∠AEF+∠CFE=180°,∠AEF-∠1=∠2,则在图中相等的角共有( )
A.5对 B.6对 C.7对 D.8对
9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于( )
A.81° B.99° C.108° D.120°
10.如图是一盏汽车探照灯纵剖面,从位于O点的灯泡发出的两束光线OB,OC经过灯碗反射以后平行射出,如果∠ABO=α,∠DCO=β,则∠BOC的度数是( )
A.α+β B.180°-α-β C.(α+β) D.90°+(α+β)
二、填空题(每题3分,共18分)
11.如图,剪刀在使用的过程中,当两个把手之间的夹角(∠DOC)增大20°时,剪刀刀刃之间的夹角(∠AOB)也相应______________,理由是______________.
12.如图,已知∠C=100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件:__________.
13.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.
14.如图,将一块含45°角的直角三角尺的直角顶点放在直尺的一边上,当∠1=35°时,则∠2的度数是________.
15.已知:如图,点M,N分别在直线AB,CD上,且AB∥CD.若在同一平面内存在一点O,使∠OMB=20°,∠OND=50°,则∠MON=________.
16.如图①是长方形纸带(对边平行),∠DEF=10°,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中∠CFE的度数是________.
三、解答题(17~20题,每题8分;21,22题,每题10分,共52分)
17.如图所示,C是河岸AB外一点.
(1)过点C要修一条与河平行的绿化带(用直线表示),请作出正确的示意图;
(2)现欲用水管从河岸AB将水引到C处,问:从河岸AB的何处开口,能使所用的水管最短?画图表示,并说明设计的理由.
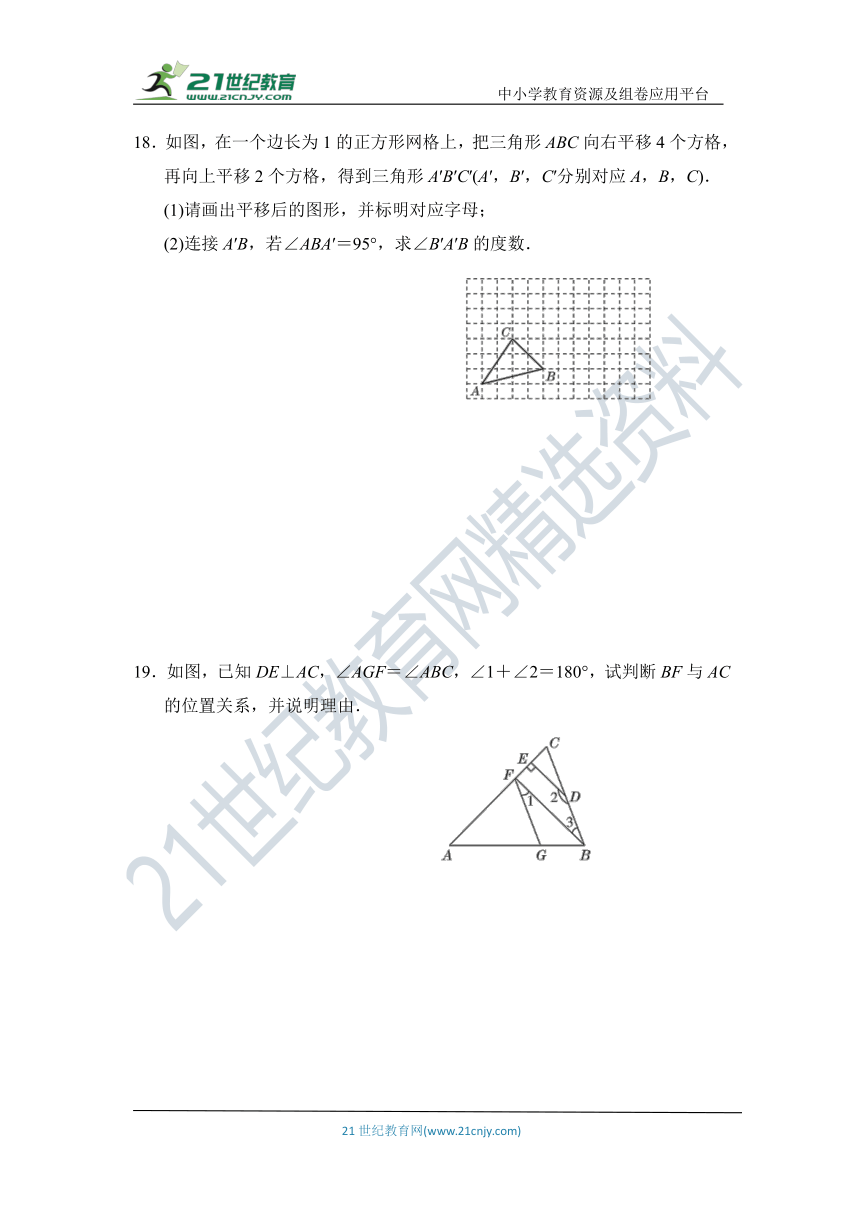
18.如图,在一个边长为1的正方形网格上,把三角形ABC向右平移4个方格,再向上平移2个方格,得到三角形A′B′C′(A′,B′,C′分别对应A,B,C).
(1)请画出平移后的图形,并标明对应字母;
(2)连接A′B,若∠ABA′=95°,求∠B′A′B的度数.
19.如图,已知DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
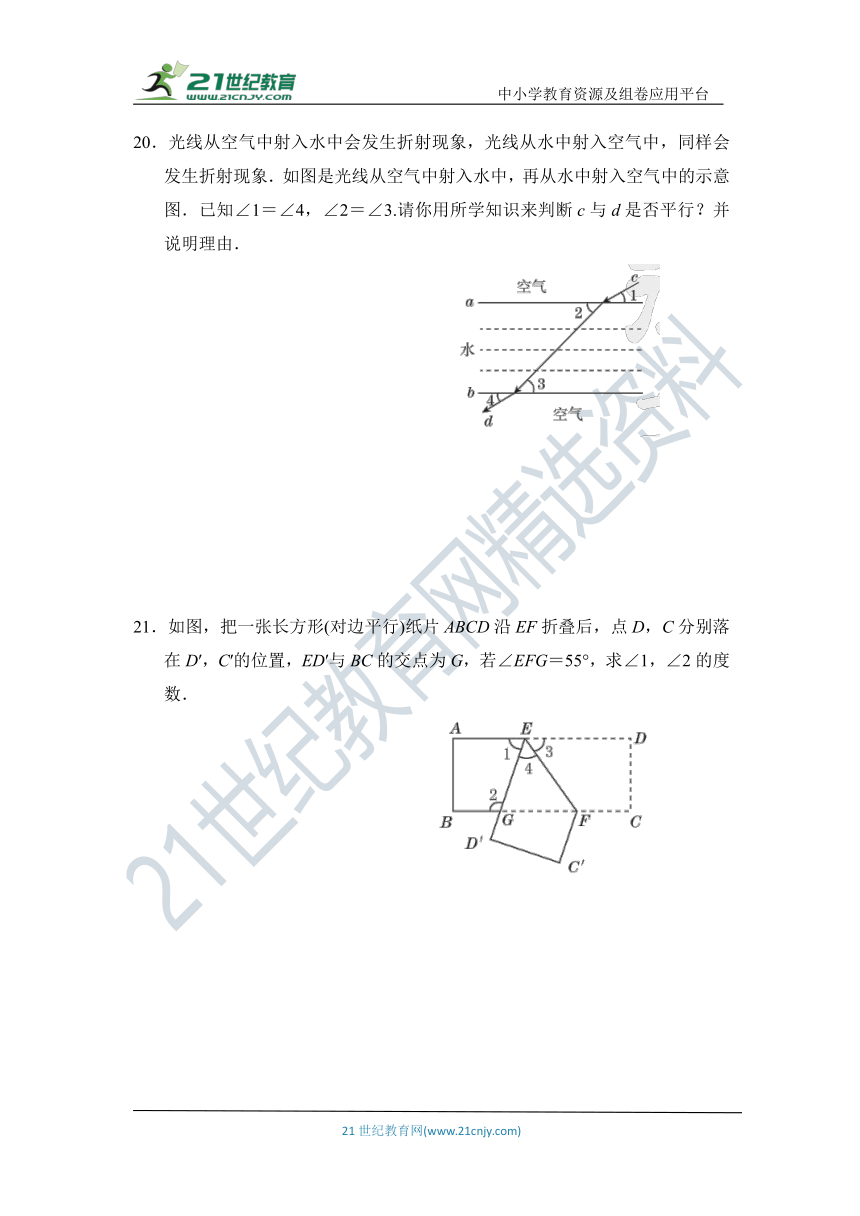
20.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行?并说明理由.
21.如图,把一张长方形(对边平行)纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
22.MN∥EF,C为两直线之间的一点.
(1)如图①,∠CAM与∠CBE的平分线相交于点D,若∠ACB=100°,求∠ADB的度数;
(2)如图②,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并说明理由;
(3)如图③,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请写出∠ACB与∠ADB的数量关系,并说明理由.
答案
一、1.C 2.A 3.D
4.B 点拨:如图所示,直线a与直线b相交于点O,在直线a的两侧分别作直线a的平行线m,n,分别交直线b于A,B两点,且与直线a的距离都为2 cm,则直线b上A,B两点到直线a的距离都为2 cm.本题易错在只在直线a的一侧作平行线,从而出现位置情况考虑不全而致错.
5.A 6.C 7.B 8.D
9.B 点拨:如图,过点B作MN∥AD,所以∠ABN=∠A=72°.因为CH∥AD,AD∥MN,所以CH∥MN,所以∠NBC+∠BCH=180°,所以∠NBC=180°-∠BCH=180°-153°=27°.所以∠ABC=∠ABN+∠NBC=72°+27°=99°.
10.A
二、11.增大20°;对顶角相等
12.∠AEC=100°(答案不唯一)
13.140°
14.80°
15.70°或30°
16.150° 点拨:在题图①中,因为AD∥BC,所以∠BFE=∠DEF=10°,则∠EFC=180°-∠BFE=170°.在题图②中,∠BFC=∠EFC-∠BFE=170°-10°=160°.在题图③中,∠CFE=∠BFC-∠BFE=160°-10°=150°.故∠CFE的度数是150°.
三、17.解:(1)如图,过点C画一条平行于AB的直线.
(2)如图,过点C作CD⊥AB于点D,从河岸AB的D处开口,能使所用的水管最短.设计理由是垂线段最短.
18.解:(1)略.
(2)因为三角形A′B′C′是由三角形ABC经过平移得到的,所以AB∥A′B′,所以∠B′A′B=∠ABA′=95°.
19.解:BF与AC的位置关系是BF⊥AC.
理由:因为∠AGF=∠ABC,
所以BC∥GF.所以∠1=∠3.
又因为∠1+∠2=180°,
所以∠2+∠3=180°.所以BF∥DE.
所以∠BFC=∠DEC.
因为DE⊥AC,所以∠DEC=90°,所以∠BFC=90°,即BF⊥AC.
20.解:c∥d.
理由:如图,
因为∠2+∠5=∠3+∠6=180°,∠2=∠3,
所以∠5=∠6.又因为∠1=∠4,
所以∠1+∠5=∠4+∠6,
所以c∥d(内错角相等,两直线平行).
21.解:因为AD∥BC,所以∠3=∠EFG=55°,∠2+∠1=180°.
由折叠的性质得∠3=∠4,
所以∠1=180°-∠3-∠4=180°-2∠3=70°,
所以∠2=180°-∠1=110°.
22.解:(1)如图①,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG.
因为∠MAC与∠EBC的平分线相交于点D,
所以∠1=∠MAC=∠ACG,∠2=∠EBC=∠BCG,
所以∠ADB=∠ADH+∠BDH=∠1+∠2=(∠ACG+∠BCG)=∠ACB.
因为∠ACB=100°,所以∠ADB=50°.
(2)∠ADB=180°-∠ACB.
理由:如图②,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠1=∠ADH,∠2=∠BDH,∠MAC+∠ACG=180°,∠BCG+∠EBC=180°,
因为∠MAC与∠EBC的平分线相交于点D,
所以∠1=∠MAC,∠2=∠EBC,
所以∠ADB=∠ADH+∠BDH=∠1+∠2=(∠MAC+∠EBC)=·(180°-∠ACG+180°-∠BCG)=(360°-∠ACB),
所以∠ADB=180°-∠ACB.
(3)∠ADB=90°-∠ACB.
理由:如图③,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠2=∠BDH,∠NAC=∠ACG,∠MAC+∠ACG=180°,∠EBC+∠BCG=180°.
因为∠MAC与∠FBC的平分线所在的直线相交于点D,
所以∠1=∠CAD=∠MAC,∠2=∠CBF,
所以∠BDH=∠CBF.
所以∠ADB=180°-∠CAD-∠CAN-∠BDH
=180°-∠MAC-∠ACG-∠CBF
=180°-∠MAC-∠ACG-(180°-∠EBC)
=180°-∠MAC-∠ACG-90°+∠EBC
=90°-(180°-∠ACG)-∠ACG+(180°-∠BCG)
=90°-90°+∠ACG-∠ACG+90°-∠BCG
=90°-∠ACG-∠BCG
=90°-(∠ACG+∠BCG)
=90°-∠ACB.
点拨:解答本题的关键是过“拐点”(折线中两条线段的公共端点)作直线的平行线,利用平行线的判定和性质探究角的度数和角的数量关系;由于条件类似,因此其解题过程也可以类比完成.
一、选择题(每题3分,共30分)
1.在下图中,∠1和∠2是对顶角的是( )
2.下面四种判定两条直线垂直的方法中,正确的有( )个.
①两条直线相交,有一个角是直角,则这两条直线互相垂直;②两条直线相交,有一组对顶角互补,则这两条直线互相垂直;③两条直线相交,四个角都相等,则这两条直线互相垂直;④两条直线相交,有一组邻补角相等,则这两条直线互相垂直.
A.4 B.3 C.2 D.1
3.如图,在6×6的方格中,图①中的图形N平移后的位置如图②所示,则下列对图形N平移方法的叙述中,正确的是( )
A.向下移动1格 B.向上移动1格
C.向上移动2格 D.向下移动2格
4.直线a与直线b相交于点O,则直线b上到直线a的距离等于2 cm的点有( )
A.1个 B.2个 C.4个 D.无数个
5.如图,在江边有一个村庄赵庄,现要建一码头,为了使赵庄人乘船最方便,请你在岸上选一点来建码头,应建在( )
A.A点 B.B点 C.C点 D.D点
6.如图,AB∥CD,FE⊥DB,垂足为点E,∠1=50°,则∠2的度数是( )
A.60° B.50° C.40° D.30°
7.如图,若将木条a绕点O旋转后使其与木条b平行,则旋转的最小角度为( )
A.65° B.85° C.95° D.115°
8.已知:如图,点E,F分别在直线AB,CD上,点G,H在两直线之间,线段EF与GH相交于点O,且有∠AEF+∠CFE=180°,∠AEF-∠1=∠2,则在图中相等的角共有( )
A.5对 B.6对 C.7对 D.8对
9.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯处的∠A是72°,第二次拐弯处的角是∠B,第三次拐弯处的∠C是153°,这时道路恰好和第一次拐弯之前的道路平行,则∠B等于( )
A.81° B.99° C.108° D.120°
10.如图是一盏汽车探照灯纵剖面,从位于O点的灯泡发出的两束光线OB,OC经过灯碗反射以后平行射出,如果∠ABO=α,∠DCO=β,则∠BOC的度数是( )
A.α+β B.180°-α-β C.(α+β) D.90°+(α+β)
二、填空题(每题3分,共18分)
11.如图,剪刀在使用的过程中,当两个把手之间的夹角(∠DOC)增大20°时,剪刀刀刃之间的夹角(∠AOB)也相应______________,理由是______________.
12.如图,已知∠C=100°,若增加一个条件,使得AB∥CD,试写出符合要求的一个条件:__________.
13.如图,直线l1∥l2,∠α=∠β,∠1=40°,则∠2=________.
14.如图,将一块含45°角的直角三角尺的直角顶点放在直尺的一边上,当∠1=35°时,则∠2的度数是________.
15.已知:如图,点M,N分别在直线AB,CD上,且AB∥CD.若在同一平面内存在一点O,使∠OMB=20°,∠OND=50°,则∠MON=________.
16.如图①是长方形纸带(对边平行),∠DEF=10°,将纸带沿EF折叠成图②,再沿BF折叠成图③,则图③中∠CFE的度数是________.
三、解答题(17~20题,每题8分;21,22题,每题10分,共52分)
17.如图所示,C是河岸AB外一点.
(1)过点C要修一条与河平行的绿化带(用直线表示),请作出正确的示意图;
(2)现欲用水管从河岸AB将水引到C处,问:从河岸AB的何处开口,能使所用的水管最短?画图表示,并说明设计的理由.
18.如图,在一个边长为1的正方形网格上,把三角形ABC向右平移4个方格,再向上平移2个方格,得到三角形A′B′C′(A′,B′,C′分别对应A,B,C).
(1)请画出平移后的图形,并标明对应字母;
(2)连接A′B,若∠ABA′=95°,求∠B′A′B的度数.
19.如图,已知DE⊥AC,∠AGF=∠ABC,∠1+∠2=180°,试判断BF与AC的位置关系,并说明理由.
20.光线从空气中射入水中会发生折射现象,光线从水中射入空气中,同样会发生折射现象.如图是光线从空气中射入水中,再从水中射入空气中的示意图.已知∠1=∠4,∠2=∠3.请你用所学知识来判断c与d是否平行?并说明理由.
21.如图,把一张长方形(对边平行)纸片ABCD沿EF折叠后,点D,C分别落在D′,C′的位置,ED′与BC的交点为G,若∠EFG=55°,求∠1,∠2的度数.
22.MN∥EF,C为两直线之间的一点.
(1)如图①,∠CAM与∠CBE的平分线相交于点D,若∠ACB=100°,求∠ADB的度数;
(2)如图②,若∠CAM与∠CBE的平分线相交于点D,∠ACB与∠ADB有何数量关系?并说明理由;
(3)如图③,若∠CAM的平分线与∠CBF的平分线所在的直线相交于点D,请写出∠ACB与∠ADB的数量关系,并说明理由.
答案
一、1.C 2.A 3.D
4.B 点拨:如图所示,直线a与直线b相交于点O,在直线a的两侧分别作直线a的平行线m,n,分别交直线b于A,B两点,且与直线a的距离都为2 cm,则直线b上A,B两点到直线a的距离都为2 cm.本题易错在只在直线a的一侧作平行线,从而出现位置情况考虑不全而致错.
5.A 6.C 7.B 8.D
9.B 点拨:如图,过点B作MN∥AD,所以∠ABN=∠A=72°.因为CH∥AD,AD∥MN,所以CH∥MN,所以∠NBC+∠BCH=180°,所以∠NBC=180°-∠BCH=180°-153°=27°.所以∠ABC=∠ABN+∠NBC=72°+27°=99°.
10.A
二、11.增大20°;对顶角相等
12.∠AEC=100°(答案不唯一)
13.140°
14.80°
15.70°或30°
16.150° 点拨:在题图①中,因为AD∥BC,所以∠BFE=∠DEF=10°,则∠EFC=180°-∠BFE=170°.在题图②中,∠BFC=∠EFC-∠BFE=170°-10°=160°.在题图③中,∠CFE=∠BFC-∠BFE=160°-10°=150°.故∠CFE的度数是150°.
三、17.解:(1)如图,过点C画一条平行于AB的直线.
(2)如图,过点C作CD⊥AB于点D,从河岸AB的D处开口,能使所用的水管最短.设计理由是垂线段最短.
18.解:(1)略.
(2)因为三角形A′B′C′是由三角形ABC经过平移得到的,所以AB∥A′B′,所以∠B′A′B=∠ABA′=95°.
19.解:BF与AC的位置关系是BF⊥AC.
理由:因为∠AGF=∠ABC,
所以BC∥GF.所以∠1=∠3.
又因为∠1+∠2=180°,
所以∠2+∠3=180°.所以BF∥DE.
所以∠BFC=∠DEC.
因为DE⊥AC,所以∠DEC=90°,所以∠BFC=90°,即BF⊥AC.
20.解:c∥d.
理由:如图,
因为∠2+∠5=∠3+∠6=180°,∠2=∠3,
所以∠5=∠6.又因为∠1=∠4,
所以∠1+∠5=∠4+∠6,
所以c∥d(内错角相等,两直线平行).
21.解:因为AD∥BC,所以∠3=∠EFG=55°,∠2+∠1=180°.
由折叠的性质得∠3=∠4,
所以∠1=180°-∠3-∠4=180°-2∠3=70°,
所以∠2=180°-∠1=110°.
22.解:(1)如图①,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠1=∠ADH,∠2=∠BDH,∠MAC=∠ACG,∠EBC=∠BCG.
因为∠MAC与∠EBC的平分线相交于点D,
所以∠1=∠MAC=∠ACG,∠2=∠EBC=∠BCG,
所以∠ADB=∠ADH+∠BDH=∠1+∠2=(∠ACG+∠BCG)=∠ACB.
因为∠ACB=100°,所以∠ADB=50°.
(2)∠ADB=180°-∠ACB.
理由:如图②,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠1=∠ADH,∠2=∠BDH,∠MAC+∠ACG=180°,∠BCG+∠EBC=180°,
因为∠MAC与∠EBC的平分线相交于点D,
所以∠1=∠MAC,∠2=∠EBC,
所以∠ADB=∠ADH+∠BDH=∠1+∠2=(∠MAC+∠EBC)=·(180°-∠ACG+180°-∠BCG)=(360°-∠ACB),
所以∠ADB=180°-∠ACB.
(3)∠ADB=90°-∠ACB.
理由:如图③,过点C作CG∥MN,过点D作DH∥MN,
因为MN∥EF,所以MN∥CG∥DH∥EF,
所以∠2=∠BDH,∠NAC=∠ACG,∠MAC+∠ACG=180°,∠EBC+∠BCG=180°.
因为∠MAC与∠FBC的平分线所在的直线相交于点D,
所以∠1=∠CAD=∠MAC,∠2=∠CBF,
所以∠BDH=∠CBF.
所以∠ADB=180°-∠CAD-∠CAN-∠BDH
=180°-∠MAC-∠ACG-∠CBF
=180°-∠MAC-∠ACG-(180°-∠EBC)
=180°-∠MAC-∠ACG-90°+∠EBC
=90°-(180°-∠ACG)-∠ACG+(180°-∠BCG)
=90°-90°+∠ACG-∠ACG+90°-∠BCG
=90°-∠ACG-∠BCG
=90°-(∠ACG+∠BCG)
=90°-∠ACB.
点拨:解答本题的关键是过“拐点”(折线中两条线段的公共端点)作直线的平行线,利用平行线的判定和性质探究角的度数和角的数量关系;由于条件类似,因此其解题过程也可以类比完成.
