沪教版(上海)初中数学七年级第一学期 11.6 轴对称形 教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 11.6 轴对称形 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 984.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
11.6轴对称
【教学目标】
1.
利用图形的翻折运动,理解轴对称的概念,知道“轴对称图形”与“两个图形关于一条直线成轴对称图形”的区别,初步感知图形变换的思想;
2.
通过操作实验,探索轴对称的基本性质,渗透化归和类比的数学思想;
3.
会用轴对称的基本性质画出简单的轴对称图形和对称轴,初步形成动态研究几何图形的意识。
【教学重点】
1.
通过图形的翻折运动,理解两个图形关于一条直线成轴对称的概念.
2.
会用轴对称的基本性质画出简单的轴对称图形和对称轴.
【教学难点】
轴对称概念的理解
【教学过程】
一、复习“轴对称图形”的概念
1.(1)下图中哪些是轴对称图形?若是,请画出它的一条对称轴,并指出它有几条对称轴?
(2)展示学生上节课后剪纸的作业
2.
复习轴对称图形的概念
【说明:通过例题复习轴对称图形的概念,进一步掌握轴对称概念,感受轴对称图形的美。同时也为本节课内容“两个图形关于一条直线成轴对称”的概念的比较作铺垫】
二、学习“两个图形关于一条直线成轴对称”的概念
1.如果把下图都看成两个图形,那么这两组图形有什么共同的特征?
归纳:轴对称的概念
把一个图形沿着某一条直线翻折,能与另一个图形重合,那么称这两个图形关于这条直线成轴对称。这条直线叫做对称轴。
【说明:结合具体实例,通过利用多媒体动画分别将以上图形从一幅图形演变成两幅图形引导学生感知成“两个图形关于一条直线成轴对称”的概念,生动形象的与轴对称图形的概念区分开来】
2.辨析轴对称图形与轴对称的区别与联系
轴对称图形
轴对称
不同点
一个图形
两个图形
相同点
沿着一条直线翻折后,直线两旁的部分能够互相重合
3.实例感知
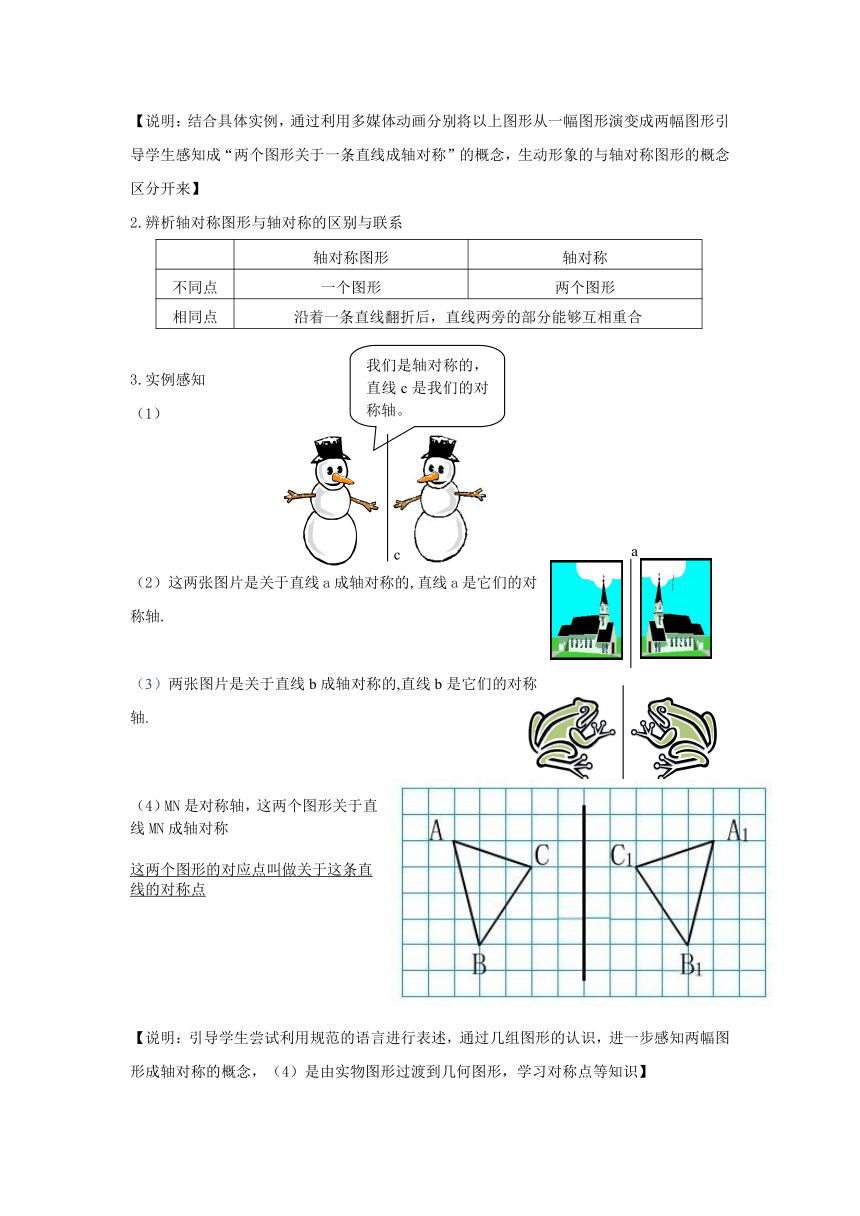
(1)
(2)这两张图片是关于直线a成轴对称的,直线a是它们的对称轴.
(3)两张图片是关于直线b成轴对称的,直线b是它们的对称轴.
(4)MN是对称轴,这两个图形关于直线MN成轴对称
这两个图形的对应点叫做关于这条直线的对称点
【说明:引导学生尝试利用规范的语言进行表述,通过几组图形的认识,进一步感知两幅图形成轴对称的概念,(4)是由实物图形过渡到几何图形,学习对称点等知识】
三、探究“两个图形关于一条直线成轴对称”的性质
1.
猜测:“两个图形关于一条直线成轴对称”的性质
(1)两个图形的形状相同,大小不变;
(2)两个图形对应线段的长度和对应角的大小相等;
(3)对应点到对称轴的距离相等(即对称轴垂直平分对称点的连线段)
2.
探索:对应角、对应线段以及对称点与对称轴之间有怎样的联系?
【说明:两个三角形沿着直线MN翻折后能够重合,探究两个三角形成轴对称的性质,利用网格便于学生发现规律。引导学生类比前面所学的知识和探索的方法。】
4、应用“两个图形关于一条直线成轴对称”的性质
1.
已知点A和直线,画出点C,使点A和点C关于直线成轴对称。
【说明:以小组讨论的形式,寻找画成轴对称的图形的方法,应用成轴对称图形的性质。】
变式1:已知线段AB和直线,画出线段CD,使线段AB和线段CD关于直线成轴对称。
变式2:已知线段AB和直线,画出线段CD,使线段AB和线段CD关于直线成轴对称。
变式3:如图,已知和直线,画出,使和关于直线成轴对称。
尝试归纳:1、画轴对称图形可以转化为画__关于直线的对称点____。
2.
画对称点的步骤:
①确定图形中的关键点(端点或顶点);
②画出关键点关于对称轴的对称点(过点作对称轴的垂线,并延长,取相等长度);
③连结关键点的对应点,得到轴对称的图形;
④结论.
【说明:画线段和三角形等关于直线l的轴对称的图形,通过一组变式练习,感受图形中的关键点在对称轴不同位置时的作图方法,进一步体悟画轴对称的图形实际就是画关于直线的对称点。尝试练习,总结画法】
2.
画出一个四边形ABCD关于直线的轴对称的图形。
【说明:独立练习,检测学生对画已知图形关于某一条直线对称的图形的掌握情况。通过一系列的变式,进一步巩固轴对称的性质。】
3.
图中的两个图形是轴对称图形,如何画出它们的对称轴呢?
归纳:画对称轴的方法
方法1:①选取两对对应点;
②分别连接两对对应点,并取中点;
③连接两个中点所得的直线就是对称轴;
④结论.
方法2:①选取一对对应点;
②连接对应点;
③画以上线段的垂直平分线就是对称轴;
④结论。
【说明:会画成轴对称的两个图形的对称轴,归纳两种方法,】
4.
请画出下图两个轴对称图形的对称轴。
五、通过这节课的学习你有什么收获和体会?还有什么疑惑吗?
T
我们是轴对称的,直线c是我们的对称轴。
c
a
b
M
N
【教学目标】
1.
利用图形的翻折运动,理解轴对称的概念,知道“轴对称图形”与“两个图形关于一条直线成轴对称图形”的区别,初步感知图形变换的思想;
2.
通过操作实验,探索轴对称的基本性质,渗透化归和类比的数学思想;
3.
会用轴对称的基本性质画出简单的轴对称图形和对称轴,初步形成动态研究几何图形的意识。
【教学重点】
1.
通过图形的翻折运动,理解两个图形关于一条直线成轴对称的概念.
2.
会用轴对称的基本性质画出简单的轴对称图形和对称轴.
【教学难点】
轴对称概念的理解
【教学过程】
一、复习“轴对称图形”的概念
1.(1)下图中哪些是轴对称图形?若是,请画出它的一条对称轴,并指出它有几条对称轴?
(2)展示学生上节课后剪纸的作业
2.
复习轴对称图形的概念
【说明:通过例题复习轴对称图形的概念,进一步掌握轴对称概念,感受轴对称图形的美。同时也为本节课内容“两个图形关于一条直线成轴对称”的概念的比较作铺垫】
二、学习“两个图形关于一条直线成轴对称”的概念
1.如果把下图都看成两个图形,那么这两组图形有什么共同的特征?
归纳:轴对称的概念
把一个图形沿着某一条直线翻折,能与另一个图形重合,那么称这两个图形关于这条直线成轴对称。这条直线叫做对称轴。
【说明:结合具体实例,通过利用多媒体动画分别将以上图形从一幅图形演变成两幅图形引导学生感知成“两个图形关于一条直线成轴对称”的概念,生动形象的与轴对称图形的概念区分开来】
2.辨析轴对称图形与轴对称的区别与联系
轴对称图形
轴对称
不同点
一个图形
两个图形
相同点
沿着一条直线翻折后,直线两旁的部分能够互相重合
3.实例感知
(1)
(2)这两张图片是关于直线a成轴对称的,直线a是它们的对称轴.
(3)两张图片是关于直线b成轴对称的,直线b是它们的对称轴.
(4)MN是对称轴,这两个图形关于直线MN成轴对称
这两个图形的对应点叫做关于这条直线的对称点
【说明:引导学生尝试利用规范的语言进行表述,通过几组图形的认识,进一步感知两幅图形成轴对称的概念,(4)是由实物图形过渡到几何图形,学习对称点等知识】
三、探究“两个图形关于一条直线成轴对称”的性质
1.
猜测:“两个图形关于一条直线成轴对称”的性质
(1)两个图形的形状相同,大小不变;
(2)两个图形对应线段的长度和对应角的大小相等;
(3)对应点到对称轴的距离相等(即对称轴垂直平分对称点的连线段)
2.
探索:对应角、对应线段以及对称点与对称轴之间有怎样的联系?
【说明:两个三角形沿着直线MN翻折后能够重合,探究两个三角形成轴对称的性质,利用网格便于学生发现规律。引导学生类比前面所学的知识和探索的方法。】
4、应用“两个图形关于一条直线成轴对称”的性质
1.
已知点A和直线,画出点C,使点A和点C关于直线成轴对称。
【说明:以小组讨论的形式,寻找画成轴对称的图形的方法,应用成轴对称图形的性质。】
变式1:已知线段AB和直线,画出线段CD,使线段AB和线段CD关于直线成轴对称。
变式2:已知线段AB和直线,画出线段CD,使线段AB和线段CD关于直线成轴对称。
变式3:如图,已知和直线,画出,使和关于直线成轴对称。
尝试归纳:1、画轴对称图形可以转化为画__关于直线的对称点____。
2.
画对称点的步骤:
①确定图形中的关键点(端点或顶点);
②画出关键点关于对称轴的对称点(过点作对称轴的垂线,并延长,取相等长度);
③连结关键点的对应点,得到轴对称的图形;
④结论.
【说明:画线段和三角形等关于直线l的轴对称的图形,通过一组变式练习,感受图形中的关键点在对称轴不同位置时的作图方法,进一步体悟画轴对称的图形实际就是画关于直线的对称点。尝试练习,总结画法】
2.
画出一个四边形ABCD关于直线的轴对称的图形。
【说明:独立练习,检测学生对画已知图形关于某一条直线对称的图形的掌握情况。通过一系列的变式,进一步巩固轴对称的性质。】
3.
图中的两个图形是轴对称图形,如何画出它们的对称轴呢?
归纳:画对称轴的方法
方法1:①选取两对对应点;
②分别连接两对对应点,并取中点;
③连接两个中点所得的直线就是对称轴;
④结论.
方法2:①选取一对对应点;
②连接对应点;
③画以上线段的垂直平分线就是对称轴;
④结论。
【说明:会画成轴对称的两个图形的对称轴,归纳两种方法,】
4.
请画出下图两个轴对称图形的对称轴。
五、通过这节课的学习你有什么收获和体会?还有什么疑惑吗?
T
我们是轴对称的,直线c是我们的对称轴。
c
a
b
M
N
