沪教版(上海)初中数学七年级第一学期 11.5 翻折与轴对称图形教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 11.5 翻折与轴对称图形教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
11.5
翻折与轴对称图形
教学目标:
知识与技能:
1、知道经过翻折运动的图形保持形状、大小不变的性质,掌握对应线段、对应角、对应点的概念,并会寻找对应元素。
2、认识轴对称图形,理解轴对称图形的概念和特征,会运用轴对称图形的概念判断一个图形是不是轴对称图形,会找出或画出轴对称图形的对称轴。
过程与方法:
通过观察,操作,总结出轴对称图形的定义,掌握判断一个图形是否是轴对称图形的方法,培养学生观察能力、抽象归纳能力和合作学习的能力。
情感与价值观:通过生活中的实例,使学生充分感知数学美,并理解数学来源于生活又服务于生活的真理,激发学生学习数学的兴趣,同时培养学生民族主义情感和爱国主义情操。
教学重点:
理解轴对称图形及找出轴对称图形的对称轴。
教学难点:
概念的形成过程及对称轴的探究过程。
1、
创设情境,激发兴趣:
欣赏图片并交流:这组图片有什么共同的特征?(图片中有很有中国特色京剧脸谱和剪纸)
师:这些图形有什么特点?
生:对称。
师:是旋转对称吗?
学:不是,是轴对称。(因为小学提到过轴对称概念,肯定会有学生回答是轴对称图形)
师:下面我们具体解释到底什么是轴对称图形?
2、
引导探究,形成新知:
1、尝试剪纸活动,理解翻折运动的意义。
活动:教师和学生每人准备好一张彩色纸,对折,任意剪出一个图形(注意,使图形与折线有相交部分,否则撕出来的两个图形就分开了)。让学生观察这个图形的特点:经过翻折后可以重合。通过剪纸时要将纸对折,让学生体会翻折这种运动。可将图形按不同位置摆放,(说明不可以说左右两旁重合)也可再使得它不对称,让学生观察(找一个对称图形,剪掉一部分,使得它不对称)。
2、学生观察、讨论、模拟概括并下定义。
定义:把一个图形沿某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。(指导学生并找关键词)
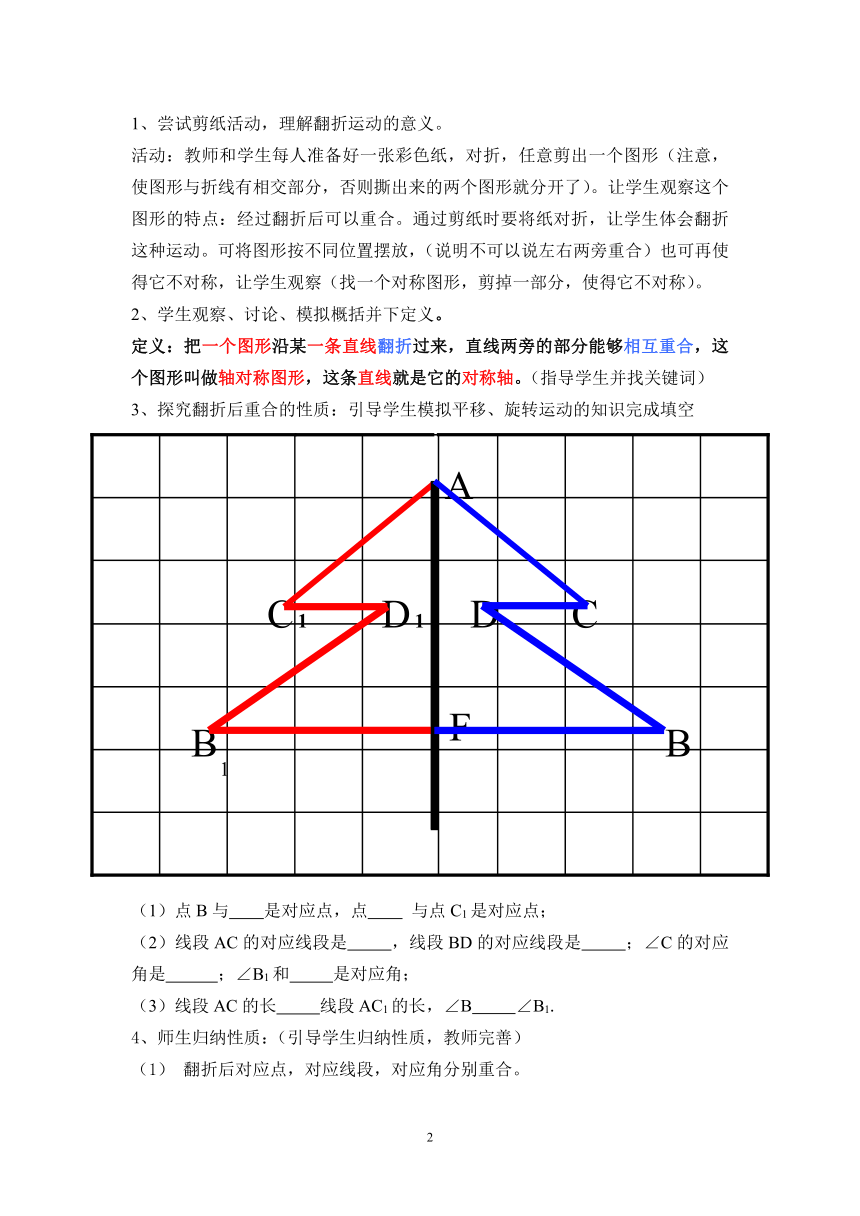
3、探究翻折后重合的性质:引导学生模拟平移、旋转运动的知识完成填空
(1)点B与
是对应点,点
与点C1是对应点;
(2)线段AC的对应线段是
,线段BD的对应线段是
;∠C的对应角是
;∠B1和
是对应角;
(3)线段AC的长
线段AC1的长,∠B
∠B1.
4、师生归纳性质:(引导学生归纳性质,教师完善)
(1)
翻折后对应点,对应线段,对应角分别重合。
(2)
对应线段长度相等,对应角大小相等。
三、轴对称图形的判断(紧扣概念)
例题:判断下列图形是否为轴对称图形(用ppt演示,体会平移,旋转,翻折运动的不同)
体会:考虑对称轴时,不要思维定势;轴对称图形的对称轴可能是一条,可能
是两条,等等。有的图形既是轴对称图形又是中心对称图形。
分析:怎么判断轴对称图形?根据定义,要沿着某条直线翻折后能完全重合。
注意:对称轴是直线,不是线段。
四、巩固练习,深化新知(采取多种学习评价方式来检测学生对新知识的理解
与掌握)
1、判断下列图形是否为轴对称图形。对的在(
)内打“√”,画出它的一条对称轴,并思考它的对称轴是不是只有一条,错的在(
)打“”。(可以互相讨论)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2、找一找
1)下列车标设计中,是轴对称图形的是
,是中心对称图形是
。
A
B
C
D
2)下列交通标志中,是轴对称图形的是
,是中心对称图形是
。
A
B
C
D
3)
0,1,2,3,4,5,6,7,8,9,十个数字中,哪些数字是轴对称图形:
。
4)找出“I
LOVE
MY
MOTHERLAND”这句英语中所有不是轴对称图形的英文字母是:
。
3、思考探究
1)选择:如图,将一块正方形纸片沿对角线对折一次,在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
2)下图是由小正方形组成的“L”形图。请你在下图中添画一个小正方形使它成为轴对称图形。
3)下列图形有什么规律,按照你发现的规律在横线上填上适当的图形。
.
五、课堂小结,回顾知识:通过本节课的学习,你有什么收获?(学生自主小结,教师完善)可以从下列角度。
1、图形的翻折及性质;
2、轴对称图形及对称轴的概念;
3、怎么判断轴对称图形,对称轴是否唯一?
4、生活中处处可见轴对称图形,而轴对称图形又被广泛应用于生活的各个方面,这充分体现了数学来源于生活,又服务于生活的真理。
六、布置作业:
必做题:练习册11.5
1、
2
拓展题:练习册11.5
3
、4
B111
F
B
C
D1
D
‘
C‘1
A‘‘‘11
1
1
1
A
B
C
D
PAGE
3
翻折与轴对称图形
教学目标:
知识与技能:
1、知道经过翻折运动的图形保持形状、大小不变的性质,掌握对应线段、对应角、对应点的概念,并会寻找对应元素。
2、认识轴对称图形,理解轴对称图形的概念和特征,会运用轴对称图形的概念判断一个图形是不是轴对称图形,会找出或画出轴对称图形的对称轴。
过程与方法:
通过观察,操作,总结出轴对称图形的定义,掌握判断一个图形是否是轴对称图形的方法,培养学生观察能力、抽象归纳能力和合作学习的能力。
情感与价值观:通过生活中的实例,使学生充分感知数学美,并理解数学来源于生活又服务于生活的真理,激发学生学习数学的兴趣,同时培养学生民族主义情感和爱国主义情操。
教学重点:
理解轴对称图形及找出轴对称图形的对称轴。
教学难点:
概念的形成过程及对称轴的探究过程。
1、
创设情境,激发兴趣:
欣赏图片并交流:这组图片有什么共同的特征?(图片中有很有中国特色京剧脸谱和剪纸)
师:这些图形有什么特点?
生:对称。
师:是旋转对称吗?
学:不是,是轴对称。(因为小学提到过轴对称概念,肯定会有学生回答是轴对称图形)
师:下面我们具体解释到底什么是轴对称图形?
2、
引导探究,形成新知:
1、尝试剪纸活动,理解翻折运动的意义。
活动:教师和学生每人准备好一张彩色纸,对折,任意剪出一个图形(注意,使图形与折线有相交部分,否则撕出来的两个图形就分开了)。让学生观察这个图形的特点:经过翻折后可以重合。通过剪纸时要将纸对折,让学生体会翻折这种运动。可将图形按不同位置摆放,(说明不可以说左右两旁重合)也可再使得它不对称,让学生观察(找一个对称图形,剪掉一部分,使得它不对称)。
2、学生观察、讨论、模拟概括并下定义。
定义:把一个图形沿某一条直线翻折过来,直线两旁的部分能够相互重合,这个图形叫做轴对称图形,这条直线就是它的对称轴。(指导学生并找关键词)
3、探究翻折后重合的性质:引导学生模拟平移、旋转运动的知识完成填空
(1)点B与
是对应点,点
与点C1是对应点;
(2)线段AC的对应线段是
,线段BD的对应线段是
;∠C的对应角是
;∠B1和
是对应角;
(3)线段AC的长
线段AC1的长,∠B
∠B1.
4、师生归纳性质:(引导学生归纳性质,教师完善)
(1)
翻折后对应点,对应线段,对应角分别重合。
(2)
对应线段长度相等,对应角大小相等。
三、轴对称图形的判断(紧扣概念)
例题:判断下列图形是否为轴对称图形(用ppt演示,体会平移,旋转,翻折运动的不同)
体会:考虑对称轴时,不要思维定势;轴对称图形的对称轴可能是一条,可能
是两条,等等。有的图形既是轴对称图形又是中心对称图形。
分析:怎么判断轴对称图形?根据定义,要沿着某条直线翻折后能完全重合。
注意:对称轴是直线,不是线段。
四、巩固练习,深化新知(采取多种学习评价方式来检测学生对新知识的理解
与掌握)
1、判断下列图形是否为轴对称图形。对的在(
)内打“√”,画出它的一条对称轴,并思考它的对称轴是不是只有一条,错的在(
)打“”。(可以互相讨论)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
(
)
2、找一找
1)下列车标设计中,是轴对称图形的是
,是中心对称图形是
。
A
B
C
D
2)下列交通标志中,是轴对称图形的是
,是中心对称图形是
。
A
B
C
D
3)
0,1,2,3,4,5,6,7,8,9,十个数字中,哪些数字是轴对称图形:
。
4)找出“I
LOVE
MY
MOTHERLAND”这句英语中所有不是轴对称图形的英文字母是:
。
3、思考探究
1)选择:如图,将一块正方形纸片沿对角线对折一次,在得到的三角形的三个角上各挖去一个圆洞,最后将正方形纸片展开,得到的图案是( )
2)下图是由小正方形组成的“L”形图。请你在下图中添画一个小正方形使它成为轴对称图形。
3)下列图形有什么规律,按照你发现的规律在横线上填上适当的图形。
.
五、课堂小结,回顾知识:通过本节课的学习,你有什么收获?(学生自主小结,教师完善)可以从下列角度。
1、图形的翻折及性质;
2、轴对称图形及对称轴的概念;
3、怎么判断轴对称图形,对称轴是否唯一?
4、生活中处处可见轴对称图形,而轴对称图形又被广泛应用于生活的各个方面,这充分体现了数学来源于生活,又服务于生活的真理。
六、布置作业:
必做题:练习册11.5
1、
2
拓展题:练习册11.5
3
、4
B111
F
B
C
D1
D
‘
C‘1
A‘‘‘11
1
1
1
A
B
C
D
PAGE
3
