苏教版三上数学 5.2从条件出发分析并解决问题(二) 教案
文档属性
| 名称 | 苏教版三上数学 5.2从条件出发分析并解决问题(二) 教案 |  | |
| 格式 | doc | ||
| 文件大小 | 339.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 06:20:50 | ||
图片预览

文档简介
解决问题的策略——从条件想起
教学内容:苏教版小学数学三年级上册第71—73页。
教学目标:
使学生在经历解决问题的过程中认识并理解“从条件想起”的策略,能初步养成边读边想的解题习惯,并主动运用这一策略解决简单的实际问题。
使学生初步经历理解题意、分析数量关系、实施解答、回顾反思的完整解题过程,进一步发展观察、综合、推理、联想能力。
在合作交流中体会解决问题方法的多样性,感受策略对于解决问题的价值,获得解决问题的成功体验。
教学重点:经历分析数量关系的过程,初步领悟从条件出发思考,分析解决实际问题的策略。
教学难点:形成能从整体上捕捉条件,积极从条件想起的策略意识。
教学过程:
一、激趣导入,初步体验:
1.猜谜活动:猜一猜老师有多高。学生意见不一时,再给出条件接着猜。
2.活动回顾:为什么一开始猜来猜去猜不对,后来一下子就猜对了?
3.揭示课题:看来借助一些相关联的条件可以帮助我们解决问题。今天我们就一起来研究怎样根据条件来解决问题。
(评析:通过游戏引发学生的思维冲突,使学生体验到:至少要两个相关联条件才能解决一个实际问题,从而明确本课的研究纬度:怎样根据条件去解决问题,并为后面的新知探究奠定良好的基础)
二、探索新知,提炼策略。
1.读题
(1)出示例题,请学生自由读题,要求用心地读,仔细地读。
(2)隐去题目,说说你读到了什么?
预设:生①什么也记不起来
生②能记住部分条件
生③能完整地记住条件和问题
(3)显示题目,校对条件和问题。
指出:读题时不仅要读出字,还要把有关的条件和问题记在脑子里,并且弄清它们的含义。
(4)请学生再次自由读题,要求边读边想:你读懂了什么?有什么问题?
(评析:两次读题的要求与目的是不同的:第一次读题在学生初次读题后,教师故意隐去已出示的题目,让学生凭记忆复述,旨在提醒学生读题时需要同时关注条件和问题;第二次再学生进行充分读题,旨在让学生在读清条件与问题的基础上,学会边读边想,理解其中的含义。利用连续两次读题的过程,引导学生学会从整体上把握条件和问题,自觉形成读题时要弄清每个条件的含义,看清要求的问题的意识)
2.理解题意
(1)有问题吧?
预设:生①没有问题。
生②“以后每天都比前一天多摘5个”这句话是什么意思?
引导:“第一天摘了30个”这个意思我明白,“以后每天都比前一天多摘5个”是什么意思? 这两个条件能让你想到什么?先自己想一想,再在小组里交流。
(2)汇报交流:①说说你的想法。
②你还能想到什么?
预设:生①第二天比第一天多摘5个,
第三天比第二天多摘5个
……
小结:还能继续说下去吗
谁能像他这样有序地说一说?
同桌互相说一说。
这么多信息用一句话概括:以后每天都比前一天多摘5个。
生②第一天摘的个数+5个=第二天的个数
第二天摘的个数+5个=第一天的个数
……
小结:还能继续说下去吗
谁能像他这样有序地说一说?
同桌互相说一说。
这么多信息也用一句话概括:以后每天都比前一天多摘5个。
生③第一天摘30个,第二天就是35个,第三天就是40个……
追问:你们都听明白了吧?他说的是什么意思?
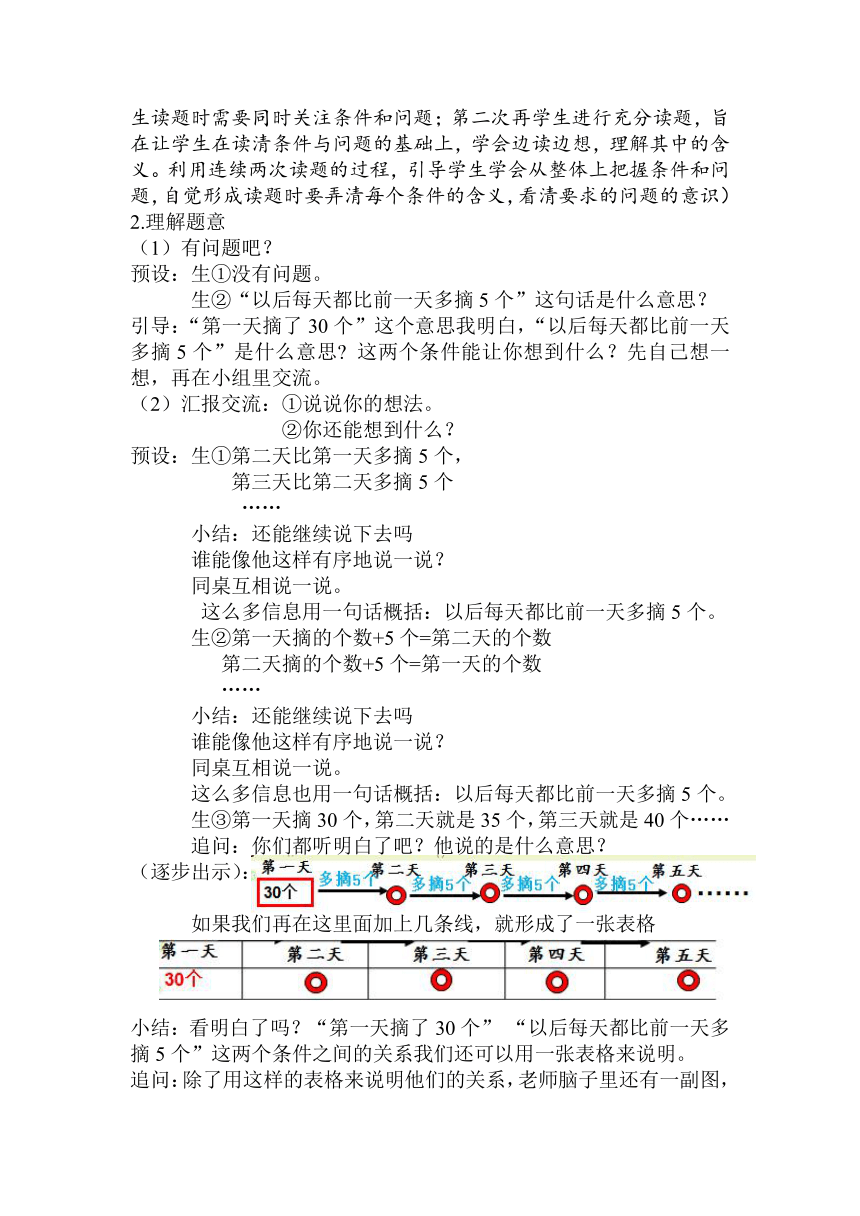
(逐步出示):
如果我们再在这里面加上几条线,就形成了一张表格
小结:看明白了吗?“第一天摘了30个” “以后每天都比前一天多摘5个”这两个条件之间的关系我们还可以用一张表格来说明。
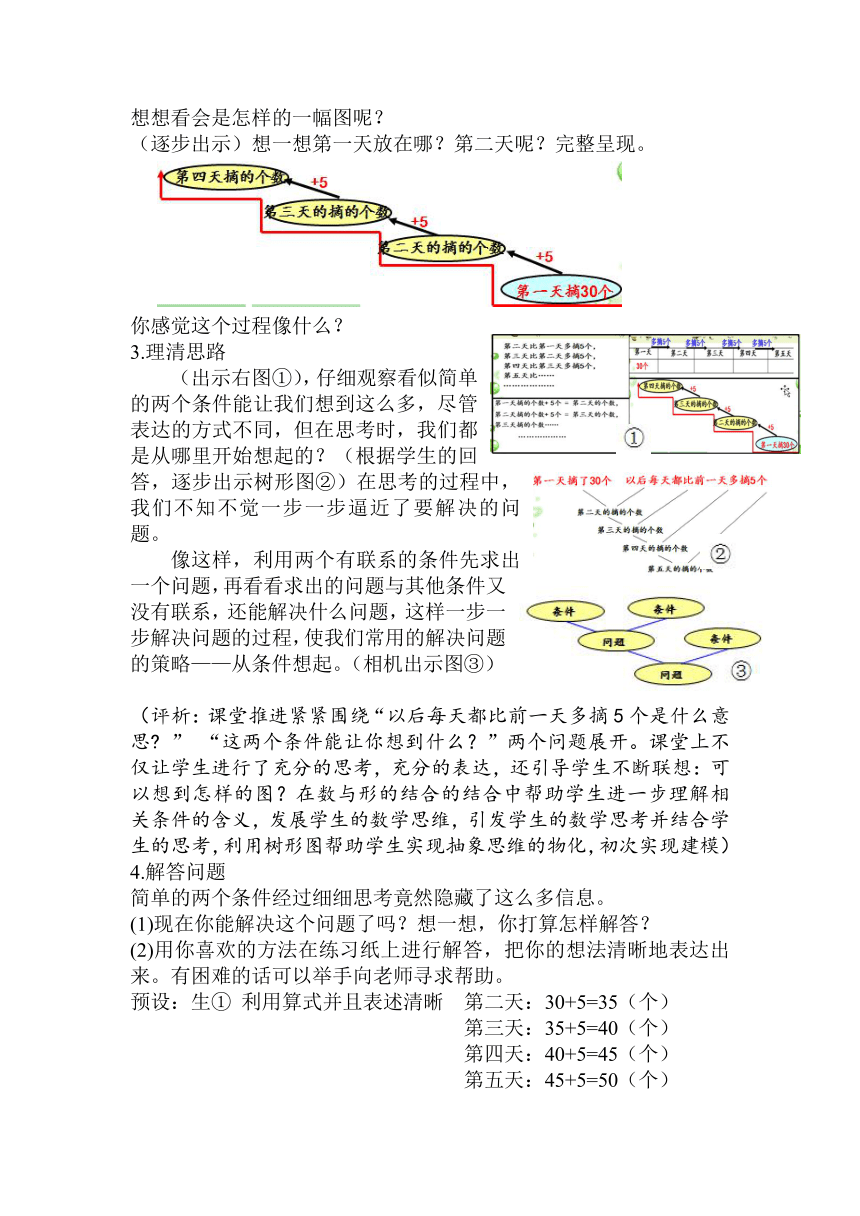
追问:除了用这样的表格来说明他们的关系,老师脑子里还有一副图,想想看会是怎样的一幅图呢?
(逐步出示)想一想第一天放在哪?第二天呢?完整呈现。
你感觉这个过程像什么?
3.理清思路
(出示右图①),仔细观察看似简单的两个条件能让我们想到这么多,尽管表达的方式不同,但在思考时,我们都是从哪里开始想起的?(根据学生的回答,逐步出示树形图②)在思考的过程中,我们不知不觉一步一步逼近了要解决的问题。
像这样,利用两个有联系的条件先求出一个问题,再看看求出的问题与其他条件又没有联系,还能解决什么问题,这样一步一步解决问题的过程,使我们常用的解决问题的策略——从条件想起。(相机出示图③)
(评析:课堂推进紧紧围绕“以后每天都比前一天多摘5个是什么意思? ” “这两个条件能让你想到什么?”两个问题展开。课堂上不仅让学生进行了充分的思考,充分的表达,还引导学生不断联想:可以想到怎样的图?在数与形的结合的结合中帮助学生进一步理解相关条件的含义,发展学生的数学思维,引发学生的数学思考并结合学生的思考,利用树形图帮助学生实现抽象思维的物化,初次实现建模)
4.解答问题
简单的两个条件经过细细思考竟然隐藏了这么多信息。
(1)现在你能解决这个问题了吗?想一想,你打算怎样解答?
(2)用你喜欢的方法在练习纸上进行解答,把你的想法清晰地表达出来。有困难的话可以举手向老师寻求帮助。
预设:生① 利用算式并且表述清晰 第二天:30+5=35(个)
第三天:35+5=40(个)
第四天:40+5=45(个)
第五天:45+5=50(个)
生② 利用算式但表述不清 30+5=35(个)
35+5=40(个)
40+5=45(个)
45+5=50(个)
生③ 不列算式,逐步进行推理 30,35,40,45,50
生④ 不列算式 利用画图(形如楼梯图)
生⑤直接寻找第三(五)天与第一天之间的关系
第三天: 30+5×2=40(个)
第五天:30+5×4=50(个)
(2)教师将不同方法进行结构化展示交流:
先同时展示生①生②
追问:两种方法你都能看懂吗?有没有什么问题?
再同时展示生③生④
追问:能看懂吗?和刚才相比,这两种方法有什么不同?
最后呈现生⑤
追问:能看懂吗?有什么问题?怎么解释?
小结:在解决问题时,我们可以根据自己的需要,可以列算式,也可以进行列表或画图。
5.回顾反思
(1)刚才我们用了不同的方法解决了这个问题,尽管方法不同,但都是先算什么?再算什么?最后算什么?(再次回归树形图)
(2)你感觉这个过程像什么?
小结:从条件想起,就像走楼梯一样,一步一步顺着想,就能找到解决问题的思路。
(3)回想一下,刚才我们是怎样一步一步解决这个问题的?
教师相机出示思维导图:读懂条件和问题——从条件想,先算什么,再算什么——列式或列表解答。
(4)追问:想一想,根据这些条件还能解决什么问题?说说你的想法?
(评析:在学生个性化运用多种方法解决问题的过程中,无论是直接推理或跳跃性性思考,树形图都为方法的得来提供了现实意义。而不同方法之间的求同思维以及问题解决后的回顾梳理,则让学生停下脚步,初步感悟:从条件想起去解决问题,是顺着条件一步一步进行推理,并初步形成对策略的完整体验;解决问题需要经历读懂条件和问题——从条件想,先算什么,再算什么——列式或列表解答这样的过程,帮助学生积累一定的数学活动经验。)
三、实践应用,丰富策略。
1、想想做做第1(1)题
(1)说说从图中你知道了哪些条件?把这些已知条件有条理地和同桌说一说。
预设:生1:4个苹果重800克。
生2:一个苹果的重量加上20克等于一个橙子的重量。
生3:一个橙子比一个苹果重20克
小结:理解了图,也就理解了其中的条件。
(2)根据已知条件可以解决什么问题?并说说你是根据哪两个条件解决这个问题的,怎样列式?
课件出示:
预设:根据“4个苹果重500克。”求出一个苹果重多少克?800/4=200
根据“一个苹果200克”和“一个橙子比一个苹果重20克”两个条件可以求出一个橙子多少克?200+20=220克
小结:一个苹果200克这个条件图中没有直接告我们,这是一个新条件。这个新条件和其他条件联系起来,我们又可以提出另一个新问题。
2、做想想做做第1(2)题。
出示:小明今年8岁,买了3盒钢笔,每盒钢笔10支,买的圆珠笔比钢笔多18支。
(1)根据这些条件你能提出一个哪些数学问题吗?
想一想,你是根据些条件来提出数学问题的?
(2)同桌交流
(3)汇报相机出示:
追问:“小明8岁”这个条件为什么一次也没有用到?
小结:在从条件想起时,我们要寻找到相关联的条件,这样才能逐步去解决问题。
3、完成“想想做做”第2题。
玩过皮球吗?一起看,弹皮球的过程中也有数学问题。
(1)出示题目及操作要求:
①先自己读题,理解题目的意思(可以画图,也可以动作表示)
②想一想,可不可以用“从条件想起”的策略来解决问题?怎么想?
③填表完成解答。
④把你的想法在小组内交流。
(2)学生汇报交流。
(评析:本课练习设计试图呈现三个层次:第1(1)小题引导学生先借助直观图提出数学问题,利用树形图再次实现从条件出发分析数量关系的建模过程,丰富对策略的认识和理解;第2(2)小题利用多余条件的介入,着重突出要寻找两个有联系的条件,并独立连续提出新问题的过程;第3题则是教师完全放手,让学生独立完整经历解决问题的过程。整个练习试图将建模过程由直观树形图的演示到凭借表象进行思考,最后达成策略的自觉应用。)
四、总结回顾,优化拓展。
1.今天学到了什么?有什么感受?
小结:事实上,从条件想起只是我们解决问题中常用的策略之一,以后随着问题的逐步复杂,我们还会接触到更多的其他策略。
(总评:本节课以解决问题为载体展开了策略教学。教师立足于学生学习的角度,引导学生逐步经历“理解题意——分析数量关系——解决问题——回顾反思”的全过程。在这个过程中,教师始终让学生处于真实的问题解决过程中,利用多种形式呈现相关条件之间的关系以及条件与问题之间的联系,引导学生经历从借助直观思考到表象思考的过程,初步建立“从条件想起”的思维模型,体会策略的价值,形成策略的意识,并能应用策略解决问题。)
教学内容:苏教版小学数学三年级上册第71—73页。
教学目标:
使学生在经历解决问题的过程中认识并理解“从条件想起”的策略,能初步养成边读边想的解题习惯,并主动运用这一策略解决简单的实际问题。
使学生初步经历理解题意、分析数量关系、实施解答、回顾反思的完整解题过程,进一步发展观察、综合、推理、联想能力。
在合作交流中体会解决问题方法的多样性,感受策略对于解决问题的价值,获得解决问题的成功体验。
教学重点:经历分析数量关系的过程,初步领悟从条件出发思考,分析解决实际问题的策略。
教学难点:形成能从整体上捕捉条件,积极从条件想起的策略意识。
教学过程:
一、激趣导入,初步体验:
1.猜谜活动:猜一猜老师有多高。学生意见不一时,再给出条件接着猜。
2.活动回顾:为什么一开始猜来猜去猜不对,后来一下子就猜对了?
3.揭示课题:看来借助一些相关联的条件可以帮助我们解决问题。今天我们就一起来研究怎样根据条件来解决问题。
(评析:通过游戏引发学生的思维冲突,使学生体验到:至少要两个相关联条件才能解决一个实际问题,从而明确本课的研究纬度:怎样根据条件去解决问题,并为后面的新知探究奠定良好的基础)
二、探索新知,提炼策略。
1.读题
(1)出示例题,请学生自由读题,要求用心地读,仔细地读。
(2)隐去题目,说说你读到了什么?
预设:生①什么也记不起来
生②能记住部分条件
生③能完整地记住条件和问题
(3)显示题目,校对条件和问题。
指出:读题时不仅要读出字,还要把有关的条件和问题记在脑子里,并且弄清它们的含义。
(4)请学生再次自由读题,要求边读边想:你读懂了什么?有什么问题?
(评析:两次读题的要求与目的是不同的:第一次读题在学生初次读题后,教师故意隐去已出示的题目,让学生凭记忆复述,旨在提醒学生读题时需要同时关注条件和问题;第二次再学生进行充分读题,旨在让学生在读清条件与问题的基础上,学会边读边想,理解其中的含义。利用连续两次读题的过程,引导学生学会从整体上把握条件和问题,自觉形成读题时要弄清每个条件的含义,看清要求的问题的意识)
2.理解题意
(1)有问题吧?
预设:生①没有问题。
生②“以后每天都比前一天多摘5个”这句话是什么意思?
引导:“第一天摘了30个”这个意思我明白,“以后每天都比前一天多摘5个”是什么意思? 这两个条件能让你想到什么?先自己想一想,再在小组里交流。
(2)汇报交流:①说说你的想法。
②你还能想到什么?
预设:生①第二天比第一天多摘5个,
第三天比第二天多摘5个
……
小结:还能继续说下去吗
谁能像他这样有序地说一说?
同桌互相说一说。
这么多信息用一句话概括:以后每天都比前一天多摘5个。
生②第一天摘的个数+5个=第二天的个数
第二天摘的个数+5个=第一天的个数
……
小结:还能继续说下去吗
谁能像他这样有序地说一说?
同桌互相说一说。
这么多信息也用一句话概括:以后每天都比前一天多摘5个。
生③第一天摘30个,第二天就是35个,第三天就是40个……
追问:你们都听明白了吧?他说的是什么意思?
(逐步出示):
如果我们再在这里面加上几条线,就形成了一张表格
小结:看明白了吗?“第一天摘了30个” “以后每天都比前一天多摘5个”这两个条件之间的关系我们还可以用一张表格来说明。
追问:除了用这样的表格来说明他们的关系,老师脑子里还有一副图,想想看会是怎样的一幅图呢?
(逐步出示)想一想第一天放在哪?第二天呢?完整呈现。
你感觉这个过程像什么?
3.理清思路
(出示右图①),仔细观察看似简单的两个条件能让我们想到这么多,尽管表达的方式不同,但在思考时,我们都是从哪里开始想起的?(根据学生的回答,逐步出示树形图②)在思考的过程中,我们不知不觉一步一步逼近了要解决的问题。
像这样,利用两个有联系的条件先求出一个问题,再看看求出的问题与其他条件又没有联系,还能解决什么问题,这样一步一步解决问题的过程,使我们常用的解决问题的策略——从条件想起。(相机出示图③)
(评析:课堂推进紧紧围绕“以后每天都比前一天多摘5个是什么意思? ” “这两个条件能让你想到什么?”两个问题展开。课堂上不仅让学生进行了充分的思考,充分的表达,还引导学生不断联想:可以想到怎样的图?在数与形的结合的结合中帮助学生进一步理解相关条件的含义,发展学生的数学思维,引发学生的数学思考并结合学生的思考,利用树形图帮助学生实现抽象思维的物化,初次实现建模)
4.解答问题
简单的两个条件经过细细思考竟然隐藏了这么多信息。
(1)现在你能解决这个问题了吗?想一想,你打算怎样解答?
(2)用你喜欢的方法在练习纸上进行解答,把你的想法清晰地表达出来。有困难的话可以举手向老师寻求帮助。
预设:生① 利用算式并且表述清晰 第二天:30+5=35(个)
第三天:35+5=40(个)
第四天:40+5=45(个)
第五天:45+5=50(个)
生② 利用算式但表述不清 30+5=35(个)
35+5=40(个)
40+5=45(个)
45+5=50(个)
生③ 不列算式,逐步进行推理 30,35,40,45,50
生④ 不列算式 利用画图(形如楼梯图)
生⑤直接寻找第三(五)天与第一天之间的关系
第三天: 30+5×2=40(个)
第五天:30+5×4=50(个)
(2)教师将不同方法进行结构化展示交流:
先同时展示生①生②
追问:两种方法你都能看懂吗?有没有什么问题?
再同时展示生③生④
追问:能看懂吗?和刚才相比,这两种方法有什么不同?
最后呈现生⑤
追问:能看懂吗?有什么问题?怎么解释?
小结:在解决问题时,我们可以根据自己的需要,可以列算式,也可以进行列表或画图。
5.回顾反思
(1)刚才我们用了不同的方法解决了这个问题,尽管方法不同,但都是先算什么?再算什么?最后算什么?(再次回归树形图)
(2)你感觉这个过程像什么?
小结:从条件想起,就像走楼梯一样,一步一步顺着想,就能找到解决问题的思路。
(3)回想一下,刚才我们是怎样一步一步解决这个问题的?
教师相机出示思维导图:读懂条件和问题——从条件想,先算什么,再算什么——列式或列表解答。
(4)追问:想一想,根据这些条件还能解决什么问题?说说你的想法?
(评析:在学生个性化运用多种方法解决问题的过程中,无论是直接推理或跳跃性性思考,树形图都为方法的得来提供了现实意义。而不同方法之间的求同思维以及问题解决后的回顾梳理,则让学生停下脚步,初步感悟:从条件想起去解决问题,是顺着条件一步一步进行推理,并初步形成对策略的完整体验;解决问题需要经历读懂条件和问题——从条件想,先算什么,再算什么——列式或列表解答这样的过程,帮助学生积累一定的数学活动经验。)
三、实践应用,丰富策略。
1、想想做做第1(1)题
(1)说说从图中你知道了哪些条件?把这些已知条件有条理地和同桌说一说。
预设:生1:4个苹果重800克。
生2:一个苹果的重量加上20克等于一个橙子的重量。
生3:一个橙子比一个苹果重20克
小结:理解了图,也就理解了其中的条件。
(2)根据已知条件可以解决什么问题?并说说你是根据哪两个条件解决这个问题的,怎样列式?
课件出示:
预设:根据“4个苹果重500克。”求出一个苹果重多少克?800/4=200
根据“一个苹果200克”和“一个橙子比一个苹果重20克”两个条件可以求出一个橙子多少克?200+20=220克
小结:一个苹果200克这个条件图中没有直接告我们,这是一个新条件。这个新条件和其他条件联系起来,我们又可以提出另一个新问题。
2、做想想做做第1(2)题。
出示:小明今年8岁,买了3盒钢笔,每盒钢笔10支,买的圆珠笔比钢笔多18支。
(1)根据这些条件你能提出一个哪些数学问题吗?
想一想,你是根据些条件来提出数学问题的?
(2)同桌交流
(3)汇报相机出示:
追问:“小明8岁”这个条件为什么一次也没有用到?
小结:在从条件想起时,我们要寻找到相关联的条件,这样才能逐步去解决问题。
3、完成“想想做做”第2题。
玩过皮球吗?一起看,弹皮球的过程中也有数学问题。
(1)出示题目及操作要求:
①先自己读题,理解题目的意思(可以画图,也可以动作表示)
②想一想,可不可以用“从条件想起”的策略来解决问题?怎么想?
③填表完成解答。
④把你的想法在小组内交流。
(2)学生汇报交流。
(评析:本课练习设计试图呈现三个层次:第1(1)小题引导学生先借助直观图提出数学问题,利用树形图再次实现从条件出发分析数量关系的建模过程,丰富对策略的认识和理解;第2(2)小题利用多余条件的介入,着重突出要寻找两个有联系的条件,并独立连续提出新问题的过程;第3题则是教师完全放手,让学生独立完整经历解决问题的过程。整个练习试图将建模过程由直观树形图的演示到凭借表象进行思考,最后达成策略的自觉应用。)
四、总结回顾,优化拓展。
1.今天学到了什么?有什么感受?
小结:事实上,从条件想起只是我们解决问题中常用的策略之一,以后随着问题的逐步复杂,我们还会接触到更多的其他策略。
(总评:本节课以解决问题为载体展开了策略教学。教师立足于学生学习的角度,引导学生逐步经历“理解题意——分析数量关系——解决问题——回顾反思”的全过程。在这个过程中,教师始终让学生处于真实的问题解决过程中,利用多种形式呈现相关条件之间的关系以及条件与问题之间的联系,引导学生经历从借助直观思考到表象思考的过程,初步建立“从条件想起”的思维模型,体会策略的价值,形成策略的意识,并能应用策略解决问题。)
同课章节目录
- 一 两、三位数乘一位数
- 整十、整百数乘一位数的口算
- 倍的认识和有关倍的简单实际问题
- 两、三位数乘一位数(不进位)的笔算
- 两、三位数乘一位数(进位)的笔算
- 两、三位数乘一位数(连续进位)的笔算
- 乘数中间、末尾有0的乘法
- 二 千克和克
- 认识千克
- 认识克
- 三 长方形和正方形
- 长方形和正方形的基本特征
- 认识周长
- 长方形和正方形周长的计算
- 周长是多少
- 四 两、三位数除以一位数
- 两、三位数除以一位数的口算
- 两、三位数除以一位数(首位能整除)的笔算
- 除法的验算
- 两、三位数除以一位数(首位不能整除)的笔算
- 商中间、末尾有0的除法
- 五 解决问题的策略
- 间隔排列
- 六 平移、旋转和轴对称
- 七 分数的初步认识(一)
- 多彩的“分数条”
