9.1.1 不等式及其解集(共37张ppt)
文档属性
| 名称 | 9.1.1 不等式及其解集(共37张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 11:13:18 | ||
图片预览










文档简介
(共37张PPT)
9.1
不等式
第1课时
不等式及其
解集
第九章
不等式与不等式组
1
课堂讲解
不等式的定义
用不等式表示数量关系
不等式的解及解集
2
课时流程
逐点
导讲练
课堂小结
课后作业
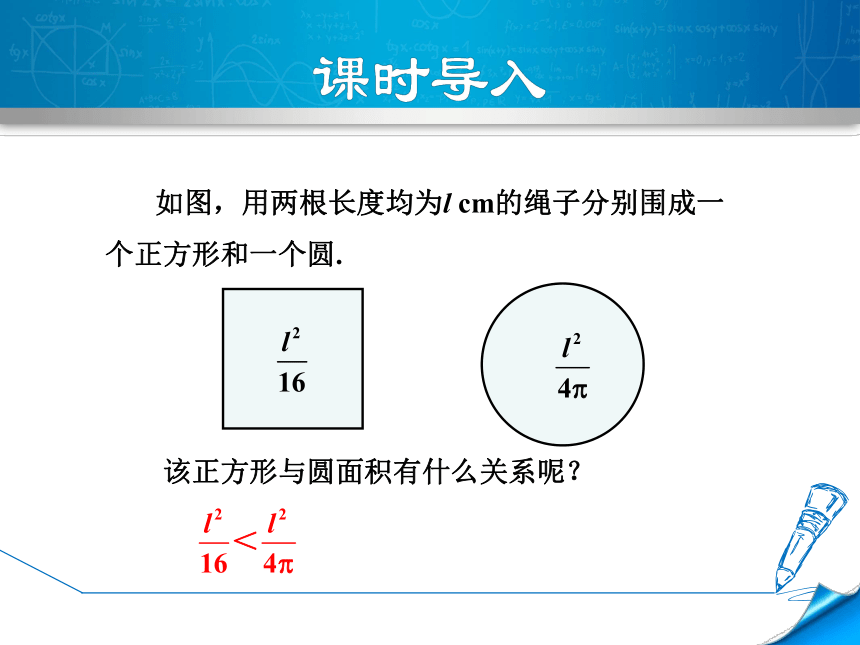
如图,用两根长度均为l
cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
1
知识点
不等式的定义
问题
一辆匀速行驶的汽车在11:20距离A
地50
km,要在12:00之前驶过A地,车速应满足什么条件?
设车速是
x
km/h.
从时间上看,汽车要在12:00之前驶过A地,
则以这个速度行驶50
km所用的时间不到
h,
即
(来自教材)
分析:
从路程上看,汽车要在12:00之前驶过A地,则
以这个速度行驶
h的
路程要超过50
km,即
式子①和②从不同角度表示了车速应满足的条
件.
(来自教材)
归
纳
(来自《教材》)
像①和②这样用符号“<”或“>”表示大小关
系的式子,叫做不等式
.
像a+2≠a-2这样用符号
“≠”表示不等关系的式子也是不等式
.
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
下列式子是不等式的有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
⑤
x>2y;⑥1≤3x+5y;⑦
;⑧
>3.
A.2个 B.3个
C.4个 D.5个
例1
导引:
判断一个式子是否为不等式的关键在于式子中是
否含有“≠”“>”“<”“≥”“≤”,由此可
知②③⑤⑥⑧是不等式.
D
总
结
一个式子是不等式,要把握两点:
一是含有不等号,
二是表示不等关系,而与不等式是否成立无关.
1
用“<”或“>”号填空.
(1)-2____2;
(2)-3____-2;
(3)12____6;
(4)0____-8;
(5)-a____a
(a>0);
(6)-a____a(a<0).
<
<
>
>
<
>
2
知识点
用不等式表示数量关系
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量;
(4)用适当的符号将各量连接起来.
列不等式:
(1)a与1的和是正数:____________;
(2)a与3的和小于-3:____________;
(3)a与-2的差大于5:____________;
(4)a的5倍小于10:____________;
(5)a的三分之一大于-7:____________.
例2
根据题中语言的叙述体现的数量关系列出式子,
然后结合体现不等关系的关键字眼列出不等式.
导引:
a+1>0
a+3<-3
a-(-2)>5
5a<10
a>-7
总
结
列不等式首先要找出表示不等关系的关键词,
然后用表示数量关系的式子表示不等式的左边和
右边.
1
用不等式表示:
(1)
a是正数;
(2)
a是负数;
(3)
a与5的和小于7;(4)
a与2的差大于-1;
(5)
a的4倍大于8;
(6)
a的一半小于3.
(来自《教材》)
(1)a>0;(2)a<0;(3)a+5<7;(4)a-2>-1;(5)4a>8;(6)
a<3.
解:
2
下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的
大于b,则
a≠b
D
3
【中考·乐山】如图,A,B两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0
B.a+b<0
C.(b-1)(a+1)>0
D.(b-1)(a-1)>0
C
4
某市某天的最高气温是33
℃,最低气温是24
℃,则该市这一天的气温t(℃)的变化范围是( )
A.t>33
B.t≤24
C.24<t<33
D.24≤t≤33
D
3
知识点
不等式的解及解集
1.不等式的解:能使不等式成立的未知数的值,
叫做不等式的解.
2.不等式的解集:一个含有未知数的不等式的
所有解,组成这个不等式的解集.
3.求不等式解集的过程叫做解不等式.
下列说法中,正确的是( )
A.
x=-3是不等式x+4<1的解
B.
x>
是不等式-2x>-3的解集
C.不等式x>-5的负整数解有无数多个
D.不等式x<7的非正整数解有无数多个
例3
D
导引:
当x=-3时,x+4=-3+4=1,所以A错;取
一个能使不等式x>
成立的值,如x=2,代
入不等式-2x>-3,发现不等式-2x>-3不
成立,故x=2不是-2x>-3的解,所以x>
不是不等式-2x>-3的解集,故B错;不等式
x>-5的负整数解只有-1,-2,-3,-4,
共4个,所以C错.
总
结
判断一个数值是不是不等式的解,只需代入验证
即可.由于不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中,因此如
果解集内有一个数能够使不等式不成立或解集外有
一个数能够使不等式成立,那么这个解集就不是这
个不等式的解集.
知识点
不等式解集在数轴上的表示法
议一议
请你用自己的方式将不等式x>5的解集和不等
式x-5≤-1的解集分别表示在数轴上,并与同伴交
流.
归
纳
(来自《教材》)
不等式x>5的解集可以用数轴上表示5的点的
右边部分来表示(如图)在数轴上表示5的点的位
置上画空心圆圈,表示5不在这个解集内.
(来自《教材》)
不等式x-5≤-1的解集x≤4可以用数轴上表
示4的点及其左边部分来表示(如图),在数轴上表
示4的点的位置上画实心圆点,表示4在这个解集内.
归
纳
不等式的解集在数轴上的表示方法:
注意:
若不等号是“≥”或“≤”,则边界点为实心圆点;若不等号是“>”或“<”,则边界点为空心圆圈.
在数轴上表示下列不等式的解集:
(1)x>2;
(2)x≤3;
(3)x<-1;
(4)x≥1.
例4
分析:
先画数轴,再定界点,最后定方向.
如图所示.
解:
总
结
(1)在定方向时,要注意不要搞错方向,大于向右.小
于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空
心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,
定界点,定方向.
1
下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12.
(来自《教材》)
3.2,4.8,8,12是不等式x+3>6的解;-4,-2.5,0,1,2.5,3不是不等式x+3>6的解.
解:
2
直接说出下列不等式的解集:
(1)
x+3>6;(2)
2x<8;(3)
x-2>0.
(来自《教材》)
(1)
x>3;
(2)
x<4;
(3)
x>2.
解:
不等式x≤3.5的正整数解是________;不等式x≥-3.5的整数解有________个,其中小于1的整数解有________________.
3
1,
2,
3
无数
-3,
-2,
-1,0
下列说法中,错误的是( )
A.不等式x<5的整数解有无数个
B.不等式x>-5的负数解有有限个
C.不等式x+4>0的解集是x>-4
D.x=-40是不等式2x<-8的一个解
4
B
下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x>2的唯一解
C.x=-2是不等式-2x>2的解集
D.x=-2,-3都是不等式-2x>2的解且
它的解有无数个
5
D
1
(中考·临夏州)在数轴上表示不等式x-1<0的解集,正确的是( )
C
2
某个关于x的不等式的解集在数轴上表示如图,则该解集是( )
A.-2<x<3
B.-2<x≤3
C.-2≤x<3
D.-2≤x≤3
B
知识方法要点
关键总结
注意事项
不等式的概念
表示不等关系的式子
注意“不大于”“不小于”的含义
列不等式
理清要比较的两个量;正确使用不等号
弄清题意,抓住关键词
不等式的解
能使不等式成立的未知数的值
指未知数的某个值
不等式的解集
一个含未知数的不等式的所有解
解集中包含了每一个不等式的解
不等式解集的表示方法
①用简单的不等式表示;②用数轴表示
界点和方向
1
知识小结
2
易错小结
“满足x<2的每一个数都是不等式x+2<5的解,所以不等式x+2<5的解集是x<2,”这句话是否正确,请你判断,并说明理由.
解:
不正确.因为x+2<5的解集是x<3,即凡是小于3的数都是不等式x+2<5的解,所以满足x<2的数只是x+2<5的部分解,故x<2不是其解集.
易错点:对不等式的解集的意义理解不透而出错
解集是不等式的所有解的集合,其中某部分解不能说成解集.
9.1
不等式
第1课时
不等式及其
解集
第九章
不等式与不等式组
1
课堂讲解
不等式的定义
用不等式表示数量关系
不等式的解及解集
2
课时流程
逐点
导讲练
课堂小结
课后作业
如图,用两根长度均为l
cm的绳子分别围成一
个正方形和一个圆.
该正方形与圆面积有什么关系呢?
1
知识点
不等式的定义
问题
一辆匀速行驶的汽车在11:20距离A
地50
km,要在12:00之前驶过A地,车速应满足什么条件?
设车速是
x
km/h.
从时间上看,汽车要在12:00之前驶过A地,
则以这个速度行驶50
km所用的时间不到
h,
即
(来自教材)
分析:
从路程上看,汽车要在12:00之前驶过A地,则
以这个速度行驶
h的
路程要超过50
km,即
式子①和②从不同角度表示了车速应满足的条
件.
(来自教材)
归
纳
(来自《教材》)
像①和②这样用符号“<”或“>”表示大小关
系的式子,叫做不等式
.
像a+2≠a-2这样用符号
“≠”表示不等关系的式子也是不等式
.
不等式的分类(按条件分):
(1)绝对不等式:任何条件下都成立的不等式,如
a2+1>0;
(2)矛盾不等式:任何条件下都不成立的不等式,如
a2+1<0;
(3)条件不等式:在一定条件下才能成立的不等式
(主要研究的不等式).
下列式子是不等式的有( )
①2x=20;②3>2;③x≠4-3;④5a+6b;
⑤
x>2y;⑥1≤3x+5y;⑦
;⑧
>3.
A.2个 B.3个
C.4个 D.5个
例1
导引:
判断一个式子是否为不等式的关键在于式子中是
否含有“≠”“>”“<”“≥”“≤”,由此可
知②③⑤⑥⑧是不等式.
D
总
结
一个式子是不等式,要把握两点:
一是含有不等号,
二是表示不等关系,而与不等式是否成立无关.
1
用“<”或“>”号填空.
(1)-2____2;
(2)-3____-2;
(3)12____6;
(4)0____-8;
(5)-a____a
(a>0);
(6)-a____a(a<0).
<
<
>
>
<
>
2
知识点
用不等式表示数量关系
列不等式的一般步骤是:
(1)分析题意,找出题目中的各种量;
(2)寻找各种量之间的不等关系;
(3)用代数式表示各量;
(4)用适当的符号将各量连接起来.
列不等式:
(1)a与1的和是正数:____________;
(2)a与3的和小于-3:____________;
(3)a与-2的差大于5:____________;
(4)a的5倍小于10:____________;
(5)a的三分之一大于-7:____________.
例2
根据题中语言的叙述体现的数量关系列出式子,
然后结合体现不等关系的关键字眼列出不等式.
导引:
a+1>0
a+3<-3
a-(-2)>5
5a<10
a>-7
总
结
列不等式首先要找出表示不等关系的关键词,
然后用表示数量关系的式子表示不等式的左边和
右边.
1
用不等式表示:
(1)
a是正数;
(2)
a是负数;
(3)
a与5的和小于7;(4)
a与2的差大于-1;
(5)
a的4倍大于8;
(6)
a的一半小于3.
(来自《教材》)
(1)a>0;(2)a<0;(3)a+5<7;(4)a-2>-1;(5)4a>8;(6)
a<3.
解:
2
下列数量关系用不等式表示错误的是( )
A.若a是负数,则a<0
B.若m的值小于1,则m<1
C.若x与-1的和大于0,则x-1>0
D.若a的
大于b,则
a≠b
D
3
【中考·乐山】如图,A,B两点在数轴上表示的数分别为a,b,下列式子成立的是( )
A.ab>0
B.a+b<0
C.(b-1)(a+1)>0
D.(b-1)(a-1)>0
C
4
某市某天的最高气温是33
℃,最低气温是24
℃,则该市这一天的气温t(℃)的变化范围是( )
A.t>33
B.t≤24
C.24<t<33
D.24≤t≤33
D
3
知识点
不等式的解及解集
1.不等式的解:能使不等式成立的未知数的值,
叫做不等式的解.
2.不等式的解集:一个含有未知数的不等式的
所有解,组成这个不等式的解集.
3.求不等式解集的过程叫做解不等式.
下列说法中,正确的是( )
A.
x=-3是不等式x+4<1的解
B.
x>
是不等式-2x>-3的解集
C.不等式x>-5的负整数解有无数多个
D.不等式x<7的非正整数解有无数多个
例3
D
导引:
当x=-3时,x+4=-3+4=1,所以A错;取
一个能使不等式x>
成立的值,如x=2,代
入不等式-2x>-3,发现不等式-2x>-3不
成立,故x=2不是-2x>-3的解,所以x>
不是不等式-2x>-3的解集,故B错;不等式
x>-5的负整数解只有-1,-2,-3,-4,
共4个,所以C错.
总
结
判断一个数值是不是不等式的解,只需代入验证
即可.由于不等式的解集必须符合两个条件:
(1)解集中的每一个数值都能使不等式成立;
(2)能够使不等式成立的所有数值都在解集中,因此如
果解集内有一个数能够使不等式不成立或解集外有
一个数能够使不等式成立,那么这个解集就不是这
个不等式的解集.
知识点
不等式解集在数轴上的表示法
议一议
请你用自己的方式将不等式x>5的解集和不等
式x-5≤-1的解集分别表示在数轴上,并与同伴交
流.
归
纳
(来自《教材》)
不等式x>5的解集可以用数轴上表示5的点的
右边部分来表示(如图)在数轴上表示5的点的位
置上画空心圆圈,表示5不在这个解集内.
(来自《教材》)
不等式x-5≤-1的解集x≤4可以用数轴上表
示4的点及其左边部分来表示(如图),在数轴上表
示4的点的位置上画实心圆点,表示4在这个解集内.
归
纳
不等式的解集在数轴上的表示方法:
注意:
若不等号是“≥”或“≤”,则边界点为实心圆点;若不等号是“>”或“<”,则边界点为空心圆圈.
在数轴上表示下列不等式的解集:
(1)x>2;
(2)x≤3;
(3)x<-1;
(4)x≥1.
例4
分析:
先画数轴,再定界点,最后定方向.
如图所示.
解:
总
结
(1)在定方向时,要注意不要搞错方向,大于向右.小
于向左.
(2)有等于号(≤,≥)画实心圆点,无等于号(<,>)画空
心圆圈.
(3)在数轴上表示不等式的解集,一般分三步:画数轴,
定界点,定方向.
1
下列数中哪些是不等式x+3>6的解?哪些不是?
-4,-2.5,0,1,2.5,3,3.2,4.8,8,12.
(来自《教材》)
3.2,4.8,8,12是不等式x+3>6的解;-4,-2.5,0,1,2.5,3不是不等式x+3>6的解.
解:
2
直接说出下列不等式的解集:
(1)
x+3>6;(2)
2x<8;(3)
x-2>0.
(来自《教材》)
(1)
x>3;
(2)
x<4;
(3)
x>2.
解:
不等式x≤3.5的正整数解是________;不等式x≥-3.5的整数解有________个,其中小于1的整数解有________________.
3
1,
2,
3
无数
-3,
-2,
-1,0
下列说法中,错误的是( )
A.不等式x<5的整数解有无数个
B.不等式x>-5的负数解有有限个
C.不等式x+4>0的解集是x>-4
D.x=-40是不等式2x<-8的一个解
4
B
下列说法中正确的是( )
A.x=1是方程-2x=2的解
B.x=-1是不等式-2x>2的唯一解
C.x=-2是不等式-2x>2的解集
D.x=-2,-3都是不等式-2x>2的解且
它的解有无数个
5
D
1
(中考·临夏州)在数轴上表示不等式x-1<0的解集,正确的是( )
C
2
某个关于x的不等式的解集在数轴上表示如图,则该解集是( )
A.-2<x<3
B.-2<x≤3
C.-2≤x<3
D.-2≤x≤3
B
知识方法要点
关键总结
注意事项
不等式的概念
表示不等关系的式子
注意“不大于”“不小于”的含义
列不等式
理清要比较的两个量;正确使用不等号
弄清题意,抓住关键词
不等式的解
能使不等式成立的未知数的值
指未知数的某个值
不等式的解集
一个含未知数的不等式的所有解
解集中包含了每一个不等式的解
不等式解集的表示方法
①用简单的不等式表示;②用数轴表示
界点和方向
1
知识小结
2
易错小结
“满足x<2的每一个数都是不等式x+2<5的解,所以不等式x+2<5的解集是x<2,”这句话是否正确,请你判断,并说明理由.
解:
不正确.因为x+2<5的解集是x<3,即凡是小于3的数都是不等式x+2<5的解,所以满足x<2的数只是x+2<5的部分解,故x<2不是其解集.
易错点:对不等式的解集的意义理解不透而出错
解集是不等式的所有解的集合,其中某部分解不能说成解集.
