沪教版(上海)数学九年级第二学期-28.1 数据整理与表示 教案
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-28.1 数据整理与表示 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 204.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 19:05:59 | ||
图片预览



文档简介
九年级数学
第二十八章
统计初步
第二学期
课题:28.1
数据整理与表示
教材分析:
学生在以前的数学学习中,已经知道有关统计的一些知识,对于数据收集和整理的方法有所了解,会画折线图、条形图和扇形图等。
在教学中要注意化解难点,在本节中,出现了复合型的条形图,教材中对此有铺垫性安排,先复习简单的条形图,再扩展到较复杂的条形图。在本节课的问题讨论中,出现的反映第五次全国人口普查时公民受教育状况的条形图,其中有三组数据,教学时要循序渐进、逐步到位。
教学目标:
1、知道条形图、折线图、扇形图各自的特点;
2、会用表格和条形图、折线图、扇形图整理与表示数据;
3、会从图表中获取各种有用信息。
教学重点:
用表格或图形表示有关数据。
教学难点:
从图表中获取相关信息。
教学过程:
一、创设情境,问题引入
观察:本章开头的统计图,它们各有怎样的特征,对于数据的分析有怎样的作用?
分析:班级组织学生参加春游,要统计人数;公司制定产品营销计划,要搞市场调查……生活中,有各种各样的“统计”。我们在小学和六年级曾经学过一些统计知识,如数据整理,求平均数,画条形图、折线图、扇形图等,知道“统计”在社会生活和工作中有广泛的应用。
“统计学”是一门科学,我们对它还需要有更多的了解。例如,报刊中经常出现各种统计图表,能否看懂这些图表?我们人口资源的状况,是国家制定发展计划的基础,那么对全国人口的基本情况进行调查,有哪些常用的方法?又如一组数据中所涉及的数往往是大小不一样,那么怎样合理表达这组数据的平均水平和波动程度?能否进一步简明地指出这组数据大致的分布情况?
【说明】章头图的背景是“中国统计年鉴”,从中选了三幅统计图,分别是条形图、折线图和扇形图。它与章头语相配合,一是说明统计知识在社会生活和生产实际中有广泛的应用;二是说明读懂有关统计图、从统计图中提取信息对每个公民有重要的意义。针对章头图,还可向学生进一步指出,统计图是在收集、整理数据的基础上绘制出来的,它所提供的信息可能是研究对象中一部分对象的信息,而且由图中直观显示的信息还可以推断一些隐含的信息。我们在本章将学习如何进行统计调查、统计分析和推断,了解总体与样本的概念、样本分析与总体估计的联系,从中体会统计的思想、方法和应用价值。章头语中还阐述了本章要讨论的问题,比如对全国人口进行调查有哪些常用方法,如何合理表达一组数据的平均水平和波动程度,以及一组数据的大致分布情况等,以引起学生学习统计的兴趣。
问题1:在2000年第五次全国人口普查中,关于我国公民受教育状况的调差结果是:每1000人中具有初中文化程度的约有340人,具有高中文化程度的约有111人,具有大学文化程度的约有36人。如何用表格和图形来表示上述统计数据?
每1000人中所占人数
初中
340
高中
111
大学
36
分析:(1)表格:
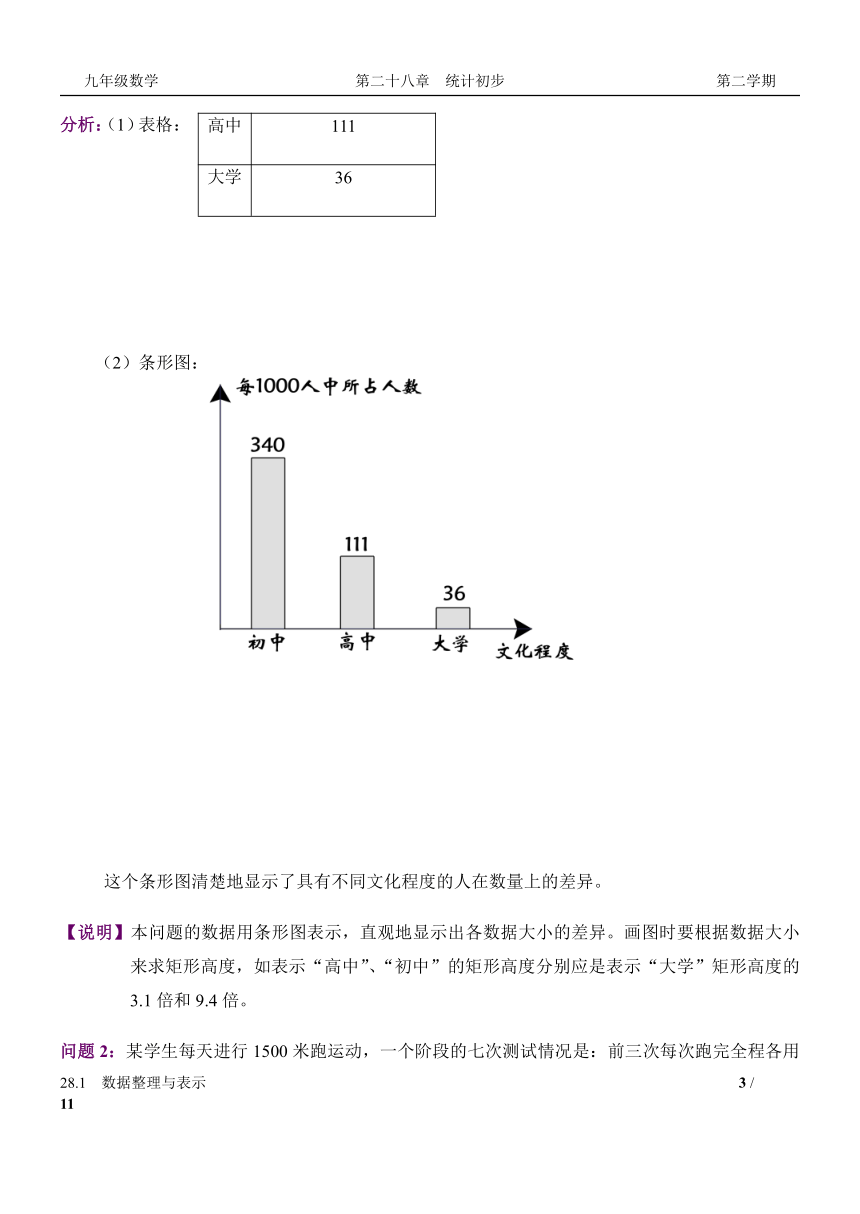
(2)条形图:
这个条形图清楚地显示了具有不同文化程度的人在数量上的差异。
【说明】本问题的数据用条形图表示,直观地显示出各数据大小的差异。画图时要根据数据大小来求矩形高度,如表示“高中”、“初中”的矩形高度分别应是表示“大学”矩形高度的3.1倍和9.4倍。
问题2:某学生每天进行1500米跑运动,一个阶段的七次测试情况是:前三次每次跑完全程各用时7分30秒,第四次用时7分钟,第五次用时6分48秒,第六次用时6分30秒,第七次用时6分18秒。如何用表格和图形的来表示上述统计数据?
测试序号
1
2
3
4
5
6
7
时间(分)
7.5
7.5
7.5
7
6.8
6.5
6.3
分析:(1)表格:
(2)折线图:
这个折线图形象地描述了这位学生1500米跑所用时间逐渐减少的情况,能“看到”坚持跑步的成效。
【说明】本问题的数据用折线图表示,直观地显示出这些数据变化的情况,在折线图中,“时间”轴上从0到5.5这一段是用带折的线显示的,这样的“简略线”表示这一段略去,从而突出这条轴上与画折线图有关的部分。这是画折线图时常用的方法。这个折线图不是函数图像,其中不涉及定义域函数图像,其中不涉及定义域的问题,故各点间用实线联结。
问题3:据调查,某校九年级有300名学生,其中30%的学生步行上学,50%的学生乘公交车上学,15%的学生骑车上学,其余的学生用其他交通工具上学。如何用表格和图形的来表示上述统计数据?
上学方式
步行
乘公交车
骑车
其他
百分比(%)
30
50
15
5
分析:(1)表格:
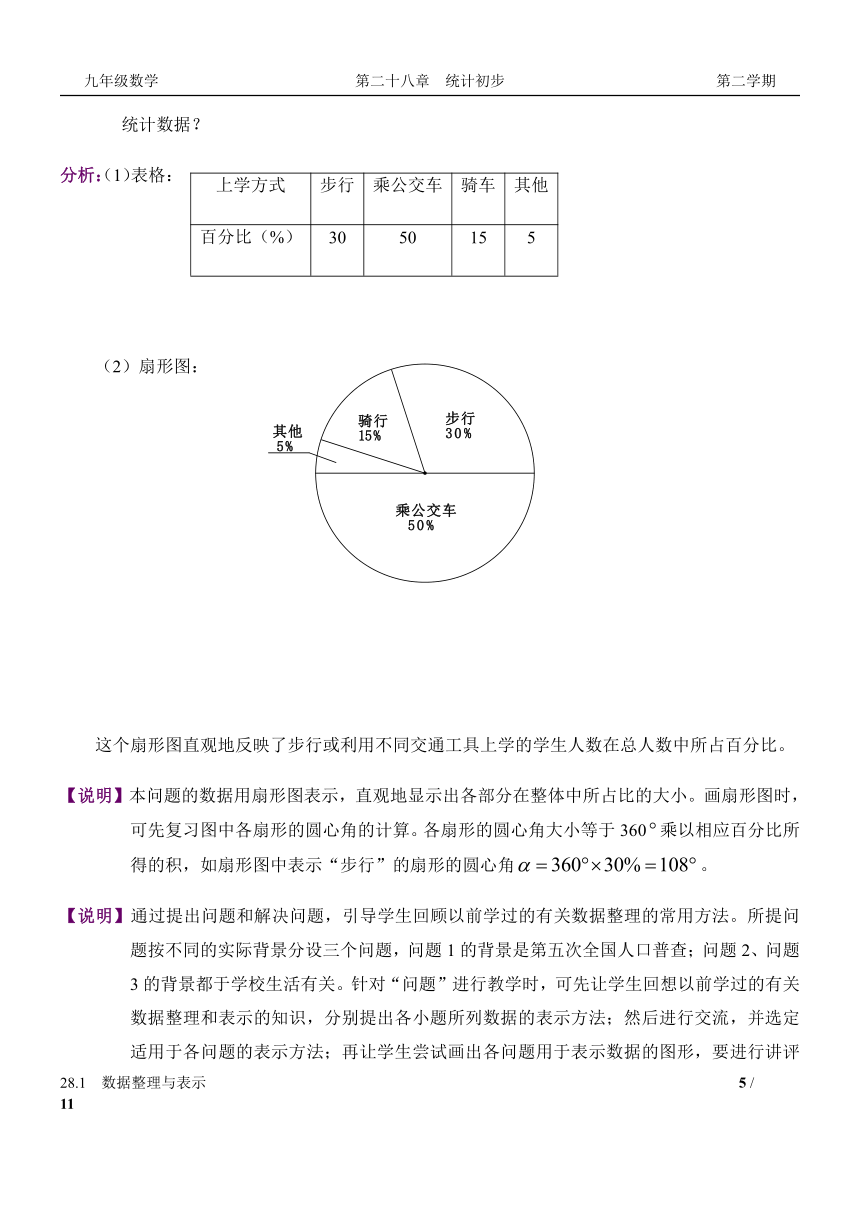
(2)扇形图:
这个扇形图直观地反映了步行或利用不同交通工具上学的学生人数在总人数中所占百分比。
【说明】本问题的数据用扇形图表示,直观地显示出各部分在整体中所占比的大小。画扇形图时,可先复习图中各扇形的圆心角的计算。各扇形的圆心角大小等于360乘以相应百分比所得的积,如扇形图中表示“步行”的扇形的圆心角。
【说明】通过提出问题和解决问题,引导学生回顾以前学过的有关数据整理的常用方法。所提问题按不同的实际背景分设三个问题,问题1的背景是第五次全国人口普查;问题2、问题3的背景都于学校生活有关。针对“问题”进行教学时,可先让学生回想以前学过的有关数据整理和表示的知识,分别提出各小题所列数据的表示方法;然后进行交流,并选定适用于各问题的表示方法;再让学生尝试画出各问题用于表示数据的图形,要进行讲评并指出画图时需要注意的事项。要让学生从中体会,统计与我们的实际生活又密切联系;表格以及条形图、折线图和扇形图,是数据整理和表示的常用方法,要注意适当选用。结合实例,指出条形图、折线图和扇形图各自的特点和长处。要让学生注意,在整理和表示数据时,可根据不同要求,选用这三种统计图中最适合一种;但选择结果往往不是唯一的。
二、学习新知,获得感悟
板书:1、统计图:(1)条形图:有利于比较数据的差异;
(2)折线图:直观地反映出数据变化的趋势;
(3)扇形图:凸显了有数据所体现出来的部分与整体的关系。
2、统计图表:表和图的简称。
三、例题选讲,训练提高
例题1、我国分别在1982年、1990年和2000年进行了第三、四、五次全国人口普查。下图是三次全国人口普查中关于公民受教育状况的统计图。
根据这个条形图,回答下列问题:
(1)从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
(2)从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少?
(3)从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加多少?
(4)从1990年到2000年,每1000人中具有大学文化程度的人数平均每年增加多少?
分析:图中初中、高中、大学每个学段都有相应三次人口普查的数据,可根据这些数据回答相应
的问题。
解:(1)233-179=54(人);
(2)111-80=31(人);
(3)(人);
(4)(人)。
答:从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加54人,
从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加31人,
从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加1人,
从1990年到2000年,每1000人中具有大学文化程度的人数平均每年增加2.2人。
问题4:如果图中只提供第四、五两次全国人口普查的有关信息,那么统计图会发生变化?
分析:图中每个文化程度的长方形要减少第三次全国人口普查的一个。
问题5:如果图中再加上第二次全国人口普查的有关信息,那么该加在图中什么地方?
分析:应该在每个文化程度的最左边加上第二次全国人口普查的相关的长方形。
问题6:本题图中突出了每种文化程度的人数在三次普查中的差异,如果要突出每次人口普查三种文化程度人数的差异,可怎样修改条形图?
分析:可将横轴改为“人口普查次序”,而将三种文化程度用不同的标识显示。
【说明】本题以我国进行的三次全国人口普查为背景,引导学生学习从统计图中获取有关信息。相对于问题1所画的条形图,本题中给出的图是复合条形图。图中横轴上,标有关于“文化程度”的“初中”、“高中”、“大学”三种程度,每种程度相应有三个矩形;结合纵轴上标有“每1000人所占人数”,可知每个矩形的高度表示每1000人中具有矩形的高度表示每1000人中具有矩形下所标文化程度的人数。由此可见,这个图是如同问题1条形图这样的三个条形图的符合,它同时提供了“三次全国人口普查”中关于公民受教育状况的信息;而且突出了每种文化程度的人数在三次普查中的差异。可先让学生读图和回答问题,然后针对学生在审题或读图中可能出现的错误进行指导,并让学生从中感受我国教育事业的迅速发展。
例题2、某企业七月份的产值的分配,画成扇形图和条形图如图所示。结合扇形图和条形图回答下列问题:
(1)该企业七月份的产值是
万元,管理成本是
万元;
(2)请将两图中缺少的部分补充完整。
解:(1)从条形图和扇形图可知,该企业七月份的生产成本为36万元,占产值的45%,所以七月份的产值为(万元);
管理成本(万元)。
(2)税前利润为。
【说明】本题通过两个不完整的统计图提供有关的统计信息,要求学生注意两个统计图之间的联系,并根据两图的信息互补来回答问题。图中的条形图和扇形图是表示同一组数据的不同图形,可引导学生先读这两个统计图,从中明确产值分配的项目及已知的有关金额或所占百分比;然后可构造表格,再寻找解决问题的突破口。注意到生产成本这一项目的金额和它占产值的百分比都是已知,于是可解第(1)小题,再完成第(2)小题。本题也可通过对两个统计图的分析,得到税前利润20万元占产值25%,然后解答第(1)小题和第(2)小题。
练习1、对某小区400户家庭中电视机类型的情况进行调查,得到如图所示的扇形图。
根据图中题中的信息,回答下列问题:
(1)拥有两台彩电的家庭有多少户?
(2)只有一台彩电的家庭有多少户?
(3)图中表示只有黑白电视机的家庭所占比例
的扇形的圆心角是多少度?
解:(1)(户);
(2)(户);
(3)。
练习2、2006年我国沿海11个城市生产总值的条形图如图所示。根据图中提供的数据,求2006年上海生产总值占沿海11个城市生产总值的百分比。(图见书上P44,3)
解:(。
答:2006年上海生产总值占沿海11个城市生产总值的百分比约为30.3%。
四、课堂小结,加深理解
1、今天我们学习了哪几种统计图?
2、每一种统计图在数据分析中各有什么优势?
五、回家作业,复习巩固
1、复习28.1
数据整理与表示,做好笔记整理;
2、完成《数学练习册》:习题28.1;
3、完成《导学案》:28.1
数据整理与表示;
4、预习《数学书》:P44-P46,28.2
统计的意义;
5、完成《导学案》:28.2
统计的意义,知识清单,课前预习。
板书设计:
教学反思:
1、能正确认识三种不同统计图及其数据表示上的优势;
2、对于简单的统计图学生都能比较容易获取信息;
3、扇形图中圆心角与百分比的关系还不十分明确。
28.1
数据整理与表示
8
/
8
第二十八章
统计初步
第二学期
课题:28.1
数据整理与表示
教材分析:
学生在以前的数学学习中,已经知道有关统计的一些知识,对于数据收集和整理的方法有所了解,会画折线图、条形图和扇形图等。
在教学中要注意化解难点,在本节中,出现了复合型的条形图,教材中对此有铺垫性安排,先复习简单的条形图,再扩展到较复杂的条形图。在本节课的问题讨论中,出现的反映第五次全国人口普查时公民受教育状况的条形图,其中有三组数据,教学时要循序渐进、逐步到位。
教学目标:
1、知道条形图、折线图、扇形图各自的特点;
2、会用表格和条形图、折线图、扇形图整理与表示数据;
3、会从图表中获取各种有用信息。
教学重点:
用表格或图形表示有关数据。
教学难点:
从图表中获取相关信息。
教学过程:
一、创设情境,问题引入
观察:本章开头的统计图,它们各有怎样的特征,对于数据的分析有怎样的作用?
分析:班级组织学生参加春游,要统计人数;公司制定产品营销计划,要搞市场调查……生活中,有各种各样的“统计”。我们在小学和六年级曾经学过一些统计知识,如数据整理,求平均数,画条形图、折线图、扇形图等,知道“统计”在社会生活和工作中有广泛的应用。
“统计学”是一门科学,我们对它还需要有更多的了解。例如,报刊中经常出现各种统计图表,能否看懂这些图表?我们人口资源的状况,是国家制定发展计划的基础,那么对全国人口的基本情况进行调查,有哪些常用的方法?又如一组数据中所涉及的数往往是大小不一样,那么怎样合理表达这组数据的平均水平和波动程度?能否进一步简明地指出这组数据大致的分布情况?
【说明】章头图的背景是“中国统计年鉴”,从中选了三幅统计图,分别是条形图、折线图和扇形图。它与章头语相配合,一是说明统计知识在社会生活和生产实际中有广泛的应用;二是说明读懂有关统计图、从统计图中提取信息对每个公民有重要的意义。针对章头图,还可向学生进一步指出,统计图是在收集、整理数据的基础上绘制出来的,它所提供的信息可能是研究对象中一部分对象的信息,而且由图中直观显示的信息还可以推断一些隐含的信息。我们在本章将学习如何进行统计调查、统计分析和推断,了解总体与样本的概念、样本分析与总体估计的联系,从中体会统计的思想、方法和应用价值。章头语中还阐述了本章要讨论的问题,比如对全国人口进行调查有哪些常用方法,如何合理表达一组数据的平均水平和波动程度,以及一组数据的大致分布情况等,以引起学生学习统计的兴趣。
问题1:在2000年第五次全国人口普查中,关于我国公民受教育状况的调差结果是:每1000人中具有初中文化程度的约有340人,具有高中文化程度的约有111人,具有大学文化程度的约有36人。如何用表格和图形来表示上述统计数据?
每1000人中所占人数
初中
340
高中
111
大学
36
分析:(1)表格:
(2)条形图:
这个条形图清楚地显示了具有不同文化程度的人在数量上的差异。
【说明】本问题的数据用条形图表示,直观地显示出各数据大小的差异。画图时要根据数据大小来求矩形高度,如表示“高中”、“初中”的矩形高度分别应是表示“大学”矩形高度的3.1倍和9.4倍。
问题2:某学生每天进行1500米跑运动,一个阶段的七次测试情况是:前三次每次跑完全程各用时7分30秒,第四次用时7分钟,第五次用时6分48秒,第六次用时6分30秒,第七次用时6分18秒。如何用表格和图形的来表示上述统计数据?
测试序号
1
2
3
4
5
6
7
时间(分)
7.5
7.5
7.5
7
6.8
6.5
6.3
分析:(1)表格:
(2)折线图:
这个折线图形象地描述了这位学生1500米跑所用时间逐渐减少的情况,能“看到”坚持跑步的成效。
【说明】本问题的数据用折线图表示,直观地显示出这些数据变化的情况,在折线图中,“时间”轴上从0到5.5这一段是用带折的线显示的,这样的“简略线”表示这一段略去,从而突出这条轴上与画折线图有关的部分。这是画折线图时常用的方法。这个折线图不是函数图像,其中不涉及定义域函数图像,其中不涉及定义域的问题,故各点间用实线联结。
问题3:据调查,某校九年级有300名学生,其中30%的学生步行上学,50%的学生乘公交车上学,15%的学生骑车上学,其余的学生用其他交通工具上学。如何用表格和图形的来表示上述统计数据?
上学方式
步行
乘公交车
骑车
其他
百分比(%)
30
50
15
5
分析:(1)表格:
(2)扇形图:
这个扇形图直观地反映了步行或利用不同交通工具上学的学生人数在总人数中所占百分比。
【说明】本问题的数据用扇形图表示,直观地显示出各部分在整体中所占比的大小。画扇形图时,可先复习图中各扇形的圆心角的计算。各扇形的圆心角大小等于360乘以相应百分比所得的积,如扇形图中表示“步行”的扇形的圆心角。
【说明】通过提出问题和解决问题,引导学生回顾以前学过的有关数据整理的常用方法。所提问题按不同的实际背景分设三个问题,问题1的背景是第五次全国人口普查;问题2、问题3的背景都于学校生活有关。针对“问题”进行教学时,可先让学生回想以前学过的有关数据整理和表示的知识,分别提出各小题所列数据的表示方法;然后进行交流,并选定适用于各问题的表示方法;再让学生尝试画出各问题用于表示数据的图形,要进行讲评并指出画图时需要注意的事项。要让学生从中体会,统计与我们的实际生活又密切联系;表格以及条形图、折线图和扇形图,是数据整理和表示的常用方法,要注意适当选用。结合实例,指出条形图、折线图和扇形图各自的特点和长处。要让学生注意,在整理和表示数据时,可根据不同要求,选用这三种统计图中最适合一种;但选择结果往往不是唯一的。
二、学习新知,获得感悟
板书:1、统计图:(1)条形图:有利于比较数据的差异;
(2)折线图:直观地反映出数据变化的趋势;
(3)扇形图:凸显了有数据所体现出来的部分与整体的关系。
2、统计图表:表和图的简称。
三、例题选讲,训练提高
例题1、我国分别在1982年、1990年和2000年进行了第三、四、五次全国人口普查。下图是三次全国人口普查中关于公民受教育状况的统计图。
根据这个条形图,回答下列问题:
(1)从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加多少?
(2)从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加多少?
(3)从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加多少?
(4)从1990年到2000年,每1000人中具有大学文化程度的人数平均每年增加多少?
分析:图中初中、高中、大学每个学段都有相应三次人口普查的数据,可根据这些数据回答相应
的问题。
解:(1)233-179=54(人);
(2)111-80=31(人);
(3)(人);
(4)(人)。
答:从第三次人口普查到第四次人口普查,每1000人中具有初中文化程度的人数增加54人,
从第四次人口普查到第五次人口普查,每1000人中具有高中文化程度的人数增加31人,
从1982年到1990年,每1000人中具有大学文化程度的人数平均每年增加1人,
从1990年到2000年,每1000人中具有大学文化程度的人数平均每年增加2.2人。
问题4:如果图中只提供第四、五两次全国人口普查的有关信息,那么统计图会发生变化?
分析:图中每个文化程度的长方形要减少第三次全国人口普查的一个。
问题5:如果图中再加上第二次全国人口普查的有关信息,那么该加在图中什么地方?
分析:应该在每个文化程度的最左边加上第二次全国人口普查的相关的长方形。
问题6:本题图中突出了每种文化程度的人数在三次普查中的差异,如果要突出每次人口普查三种文化程度人数的差异,可怎样修改条形图?
分析:可将横轴改为“人口普查次序”,而将三种文化程度用不同的标识显示。
【说明】本题以我国进行的三次全国人口普查为背景,引导学生学习从统计图中获取有关信息。相对于问题1所画的条形图,本题中给出的图是复合条形图。图中横轴上,标有关于“文化程度”的“初中”、“高中”、“大学”三种程度,每种程度相应有三个矩形;结合纵轴上标有“每1000人所占人数”,可知每个矩形的高度表示每1000人中具有矩形的高度表示每1000人中具有矩形下所标文化程度的人数。由此可见,这个图是如同问题1条形图这样的三个条形图的符合,它同时提供了“三次全国人口普查”中关于公民受教育状况的信息;而且突出了每种文化程度的人数在三次普查中的差异。可先让学生读图和回答问题,然后针对学生在审题或读图中可能出现的错误进行指导,并让学生从中感受我国教育事业的迅速发展。
例题2、某企业七月份的产值的分配,画成扇形图和条形图如图所示。结合扇形图和条形图回答下列问题:
(1)该企业七月份的产值是
万元,管理成本是
万元;
(2)请将两图中缺少的部分补充完整。
解:(1)从条形图和扇形图可知,该企业七月份的生产成本为36万元,占产值的45%,所以七月份的产值为(万元);
管理成本(万元)。
(2)税前利润为。
【说明】本题通过两个不完整的统计图提供有关的统计信息,要求学生注意两个统计图之间的联系,并根据两图的信息互补来回答问题。图中的条形图和扇形图是表示同一组数据的不同图形,可引导学生先读这两个统计图,从中明确产值分配的项目及已知的有关金额或所占百分比;然后可构造表格,再寻找解决问题的突破口。注意到生产成本这一项目的金额和它占产值的百分比都是已知,于是可解第(1)小题,再完成第(2)小题。本题也可通过对两个统计图的分析,得到税前利润20万元占产值25%,然后解答第(1)小题和第(2)小题。
练习1、对某小区400户家庭中电视机类型的情况进行调查,得到如图所示的扇形图。
根据图中题中的信息,回答下列问题:
(1)拥有两台彩电的家庭有多少户?
(2)只有一台彩电的家庭有多少户?
(3)图中表示只有黑白电视机的家庭所占比例
的扇形的圆心角是多少度?
解:(1)(户);
(2)(户);
(3)。
练习2、2006年我国沿海11个城市生产总值的条形图如图所示。根据图中提供的数据,求2006年上海生产总值占沿海11个城市生产总值的百分比。(图见书上P44,3)
解:(。
答:2006年上海生产总值占沿海11个城市生产总值的百分比约为30.3%。
四、课堂小结,加深理解
1、今天我们学习了哪几种统计图?
2、每一种统计图在数据分析中各有什么优势?
五、回家作业,复习巩固
1、复习28.1
数据整理与表示,做好笔记整理;
2、完成《数学练习册》:习题28.1;
3、完成《导学案》:28.1
数据整理与表示;
4、预习《数学书》:P44-P46,28.2
统计的意义;
5、完成《导学案》:28.2
统计的意义,知识清单,课前预习。
板书设计:
教学反思:
1、能正确认识三种不同统计图及其数据表示上的优势;
2、对于简单的统计图学生都能比较容易获取信息;
3、扇形图中圆心角与百分比的关系还不十分明确。
28.1
数据整理与表示
8
/
8
