沪教版(上海)数学八年级第二学期-22.2 平行四边形(2) 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.2 平行四边形(2) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 118.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览

文档简介
§22.2
平行四边形(2)
教学目标:
1.
经历平行四边形性质定理3、4的探索过程,从中感受图形的分解与组合的数学思想.
2.掌握平行四边形的性质定理3、4,能运用这些性质定理3、4进行证明或计算.
教学重点及难点:
平行四边形性质定理3、4的运用.
教学过程:
教师活动
学生活动
设计意图
Yi
一、复习引入问1:上节课,我们学行四边形,那么什么叫做平行四边形?问2:我们已经学行四边形的哪些性质?学习新知上节课我们从边、角讨论了平行四边形的性质,这节课我们再从对角线和对称性来讨论它的特点.问1:如图,□ABCD,有多少对全等的三角形?是哪几对?问2:由这些三角形全等,可得平行四边形的对角线什么特点?得性质定理3:平行四边形的两条对角线互相平分.问3:平行四边形ABCD具有某种对称性吗?得性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点.平行四边形的性质定理是推理的依据,下面我们举例来说明它们的基本运用.新知运用1、已知如图,在□ABCD中,对角线AC、BD相交于点O,
EF过点O且与边AB、CD分别相交于点E、F求证:OE
=
OF
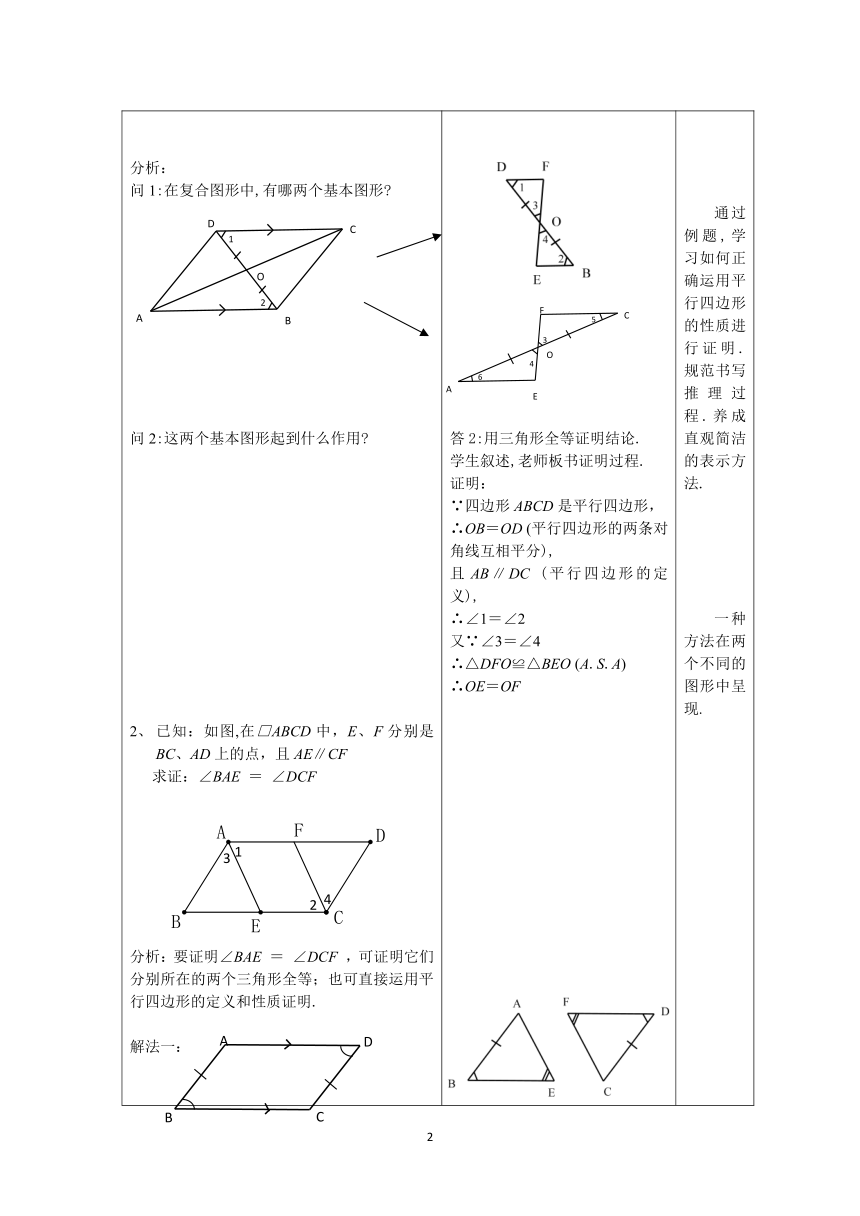
分析:问1:在复合图形中,有哪两个基本图形?问2:这两个基本图形起到什么作用?已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE
=
∠DCF
分析:要证明∠BAE
=
∠DCF
,可证明它们分别所在的两个三角形全等;也可直接运用平行四边形的定义和性质证明.
解法一:解法二:四、课堂练习1.□ABCD
中,AD=
4cm,AC
=
10cm,BD
=
6cm,ΔAOD的周长和面积各是多少?ΔAOD和ΔAOB的面积有什么关系?2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A
(3,2)、B
(–
2,1),试写出C、D两点的坐标.
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,求证:E是BF的中点,D是AF的中点.分析:
五、
本课小结:通过这节课的学习,你有什么收获或体会?1.从边、角、对角线和对称性四个方面研究.2.解题关键是找出复合图形中的基本图形,理清思路.六、
布置作业:练习册
第37页
习题22.2(2)
预设:答1:两组对边分别平行的四边形叫做平行四边形.答2:边:对边平行、对边相等.角:对角相等.邻角互补、内角和360°预设:答1:有4对.△AOD≌△COB
△AOB≌△COD
△ACD≌△CAB
△ABD≌△CDB答2:(1)AO=CO,BO=DO(2)平行四边形的两条对角线互相平分.答3:
平行四边形是中心对称图形,对称中心是两条对角线的交点.答2:用三角形全等证明结论.学生叙述,老师板书证明过程.证明:∵四边形ABCD是平行四边形,∴OB=OD
(平行四边形的两条对角线互相平分),且AB∥DC
(平行四边形的定义),∴∠1=∠2又∵∠3=∠4∴△DFO≌△BEO
(A.S.A)∴OE=OF证明:∵四边形ABCD是平行四边形,∴AD∥BC
(平行四边形的定义)∠BAD=∠DCB
(平行四边形的对角相等)又∵AE∥CF∴四边形AECF是平行四边形(平行四边形的定义)。得∠1=∠2(平行四边形的对角相等)∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠BAE=∠DCF预设学生回答:
ΔAOD的周长是12
cm,ΔAOD和ΔAOB的面积相等.(等底同高)预设学生回答:C
(-3,-2)、D
(2,-1)证明:∵E为CD的中点∴DE=CE∵四边形ABCD是平行四边形,∴AD=BC
(平行四边形对边相等)且AD∥BC
(平行四边形定义)∴∠F=∠1,∠3=∠2∴⊿FDE≌⊿BCE
(A.A.S)∴EF=EB,DF=BC∵AD=BC∴AD=DF又∵EF=EB∴E是BF的中点,D是AF的中点.预设学生回答:平行四边形的性质:边:对边平行、对边相等.角:对角相等.对角线:互相平分.对称性:是中心对称图形,对称中心是两条对角线的交点.
复习平行四边形的概念和已学的性质为下一步的学习进行铺垫.引出课题老师引导学生经历平行四边形性质定理3、4的探索过程.通过例题,学习如何正确运用平行四边形的性质进行证明.
规范书写推理过程.养成直观简洁的表示方法.一种方法在两个不同的图形中呈现.再次强调运用平行四边形的性质解决几何问题.帮助学生复习平面直角坐标系中两点关于原点对称的关系.养成从复合图形中分解出基本图形的习惯.提醒学生书写的规范性.梳理知识点,培养学生归纳反思的能力.
C
2
1
O
D
B
A
6
5
4
3
A
C
E
F
O
1
2
3
4
D
C
B
A
1
2
E
F
C
A
D
C
B
A
C
A
B
D
AD=BC
△FDE≌⊿BCE
EF=EB
点E是BF的中点
DF=BC
点D是AF的中点
PAGE
3
平行四边形(2)
教学目标:
1.
经历平行四边形性质定理3、4的探索过程,从中感受图形的分解与组合的数学思想.
2.掌握平行四边形的性质定理3、4,能运用这些性质定理3、4进行证明或计算.
教学重点及难点:
平行四边形性质定理3、4的运用.
教学过程:
教师活动
学生活动
设计意图
Yi
一、复习引入问1:上节课,我们学行四边形,那么什么叫做平行四边形?问2:我们已经学行四边形的哪些性质?学习新知上节课我们从边、角讨论了平行四边形的性质,这节课我们再从对角线和对称性来讨论它的特点.问1:如图,□ABCD,有多少对全等的三角形?是哪几对?问2:由这些三角形全等,可得平行四边形的对角线什么特点?得性质定理3:平行四边形的两条对角线互相平分.问3:平行四边形ABCD具有某种对称性吗?得性质定理4:平行四边形是中心对称图形,对称中心是两条对角线的交点.平行四边形的性质定理是推理的依据,下面我们举例来说明它们的基本运用.新知运用1、已知如图,在□ABCD中,对角线AC、BD相交于点O,
EF过点O且与边AB、CD分别相交于点E、F求证:OE
=
OF
分析:问1:在复合图形中,有哪两个基本图形?问2:这两个基本图形起到什么作用?已知:如图,在□ABCD中,E、F分别是BC、AD上的点,且AE∥CF
求证:∠BAE
=
∠DCF
分析:要证明∠BAE
=
∠DCF
,可证明它们分别所在的两个三角形全等;也可直接运用平行四边形的定义和性质证明.
解法一:解法二:四、课堂练习1.□ABCD
中,AD=
4cm,AC
=
10cm,BD
=
6cm,ΔAOD的周长和面积各是多少?ΔAOD和ΔAOB的面积有什么关系?2.在平面直角坐标系中,□ABCD的对角线的交点正好与坐标原点重合,且点A、B的坐标分别为A
(3,2)、B
(–
2,1),试写出C、D两点的坐标.
3.已知:如图,在□ABCD中,E为CD的中点,联结BE并延长,交AD的延长线于点F,求证:E是BF的中点,D是AF的中点.分析:
五、
本课小结:通过这节课的学习,你有什么收获或体会?1.从边、角、对角线和对称性四个方面研究.2.解题关键是找出复合图形中的基本图形,理清思路.六、
布置作业:练习册
第37页
习题22.2(2)
预设:答1:两组对边分别平行的四边形叫做平行四边形.答2:边:对边平行、对边相等.角:对角相等.邻角互补、内角和360°预设:答1:有4对.△AOD≌△COB
△AOB≌△COD
△ACD≌△CAB
△ABD≌△CDB答2:(1)AO=CO,BO=DO(2)平行四边形的两条对角线互相平分.答3:
平行四边形是中心对称图形,对称中心是两条对角线的交点.答2:用三角形全等证明结论.学生叙述,老师板书证明过程.证明:∵四边形ABCD是平行四边形,∴OB=OD
(平行四边形的两条对角线互相平分),且AB∥DC
(平行四边形的定义),∴∠1=∠2又∵∠3=∠4∴△DFO≌△BEO
(A.S.A)∴OE=OF证明:∵四边形ABCD是平行四边形,∴AD∥BC
(平行四边形的定义)∠BAD=∠DCB
(平行四边形的对角相等)又∵AE∥CF∴四边形AECF是平行四边形(平行四边形的定义)。得∠1=∠2(平行四边形的对角相等)∵∠3=∠BAD-∠1
∠4=∠DCB-∠2
∴∠BAE=∠DCF预设学生回答:
ΔAOD的周长是12
cm,ΔAOD和ΔAOB的面积相等.(等底同高)预设学生回答:C
(-3,-2)、D
(2,-1)证明:∵E为CD的中点∴DE=CE∵四边形ABCD是平行四边形,∴AD=BC
(平行四边形对边相等)且AD∥BC
(平行四边形定义)∴∠F=∠1,∠3=∠2∴⊿FDE≌⊿BCE
(A.A.S)∴EF=EB,DF=BC∵AD=BC∴AD=DF又∵EF=EB∴E是BF的中点,D是AF的中点.预设学生回答:平行四边形的性质:边:对边平行、对边相等.角:对角相等.对角线:互相平分.对称性:是中心对称图形,对称中心是两条对角线的交点.
复习平行四边形的概念和已学的性质为下一步的学习进行铺垫.引出课题老师引导学生经历平行四边形性质定理3、4的探索过程.通过例题,学习如何正确运用平行四边形的性质进行证明.
规范书写推理过程.养成直观简洁的表示方法.一种方法在两个不同的图形中呈现.再次强调运用平行四边形的性质解决几何问题.帮助学生复习平面直角坐标系中两点关于原点对称的关系.养成从复合图形中分解出基本图形的习惯.提醒学生书写的规范性.梳理知识点,培养学生归纳反思的能力.
C
2
1
O
D
B
A
6
5
4
3
A
C
E
F
O
1
2
3
4
D
C
B
A
1
2
E
F
C
A
D
C
B
A
C
A
B
D
AD=BC
△FDE≌⊿BCE
EF=EB
点E是BF的中点
DF=BC
点D是AF的中点
PAGE
3
