沪教版(上海)数学八年级第二学期-20.1 一次函数的概念 课件(共16张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-20.1 一次函数的概念 课件(共16张ppt) |
|
|
| 格式 | zip | ||
| 文件大小 | 597.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览






文档简介
(共16张PPT)
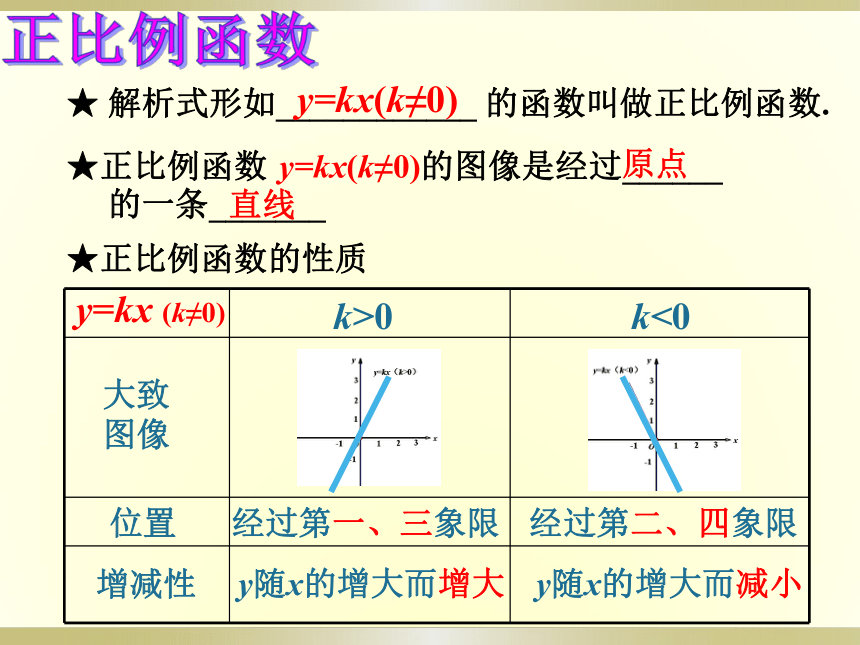
★正比例函数的性质
★
解析式形如____________
的函数叫做正比例函数.
★正比例函数
y=kx(k≠0)的图像是经过______
的一条_______
正比例函数
y=kx(k≠0)
原点
y=kx
(k≠0)
大致图像
位置
增减性
k>0
经过第一、三象限
y随x的增大而增大
k<0
经过第二、四象限
y随x的增大而减小
直线
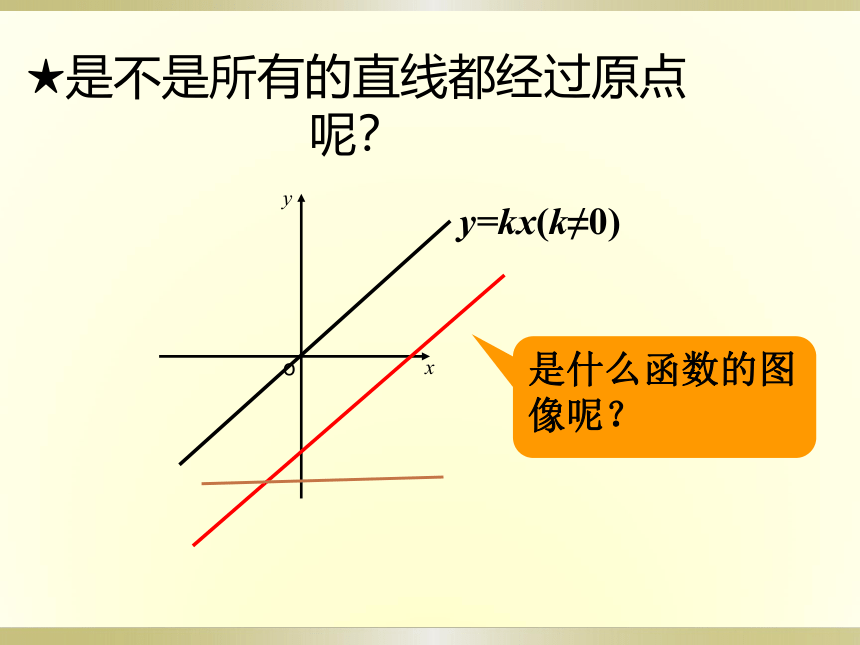
★是不是所有的直线都经过原点呢?
x
y
o
y=kx(k≠0)
是什么函数的图像呢?
第二十章
一次函数
20.1一次函数的概念
思考
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
(1)有人发现,在一定温度下,蟋蟀每分钟鸣叫次数m
与温度
t
(℃)有关,m的值大约是
t
的7倍与35的差。求m与t
的函数解析式
这个函数与正比例函数有何不同?
思考
(2)某城市的本地固定电话的月话费y(元)包括月租费与计时费。月租费为25元,计时费按照每分钟0.1元收取。设小明这个月打了x分钟的电话,求y与x的函数解析式。
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
这个函数与正比例函数有何不同?
思考
(3)一辆汽车行驶在高速公路上,汽车油箱里原有汽油120升,每行驶10千米耗油2升。设汽车行驶的路程为x千米,油箱里剩余的油量为
y升,求y与x的函数解析式。
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
思考
y
=
x
k(常数)
+b(常数)
函数解析式都是关于自变量x的一次整式
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
问:一次函数与正比例函数有什么关系?
新知
一次函数
解析式形如y=kx+b(k、b都是常数,且k≠0)函数叫做一次函数。
一次函数y=kx+b的定义域x取一切实数。
一次函数y=kx+b(k≠0)
则y=kx(k≠0)
正比例函数是一次函数的特例。
当b=0时,
例1
根据变量x、y的关系式,判断y是否是x的一次函数。如果是一次函数,分别指出常数k和b的值。
√
×
√
√
×
×
1、自变量x在分子上(整式)
2、自变量x的指数为1(一次)
例1
根据变量x、y的关系式,判断y是否是x的一次函数。如果是一次函数,分别指出常数k和b的值。
其中哪些是正比例函数?
√
√
√
1、(口答)下列函数中,哪些是一次函数?
课堂练习
课本第3页,练习20.1
/
1.
(4)y=kx+b(k、b是常数).
不是;
是
;
不是;
不是.
k
≠0?
练习:
例2
(1)若
是一次函数,则a满足
的条件是__________
分析:k≠0,即a-2≠0
解得
a≠2
k是什么?
例2
(2)已知变量x、y之间的关系式是
y=(a+1)x+a(其中a是常数)
那么y是x的一次函数吗?
分析:①当a+1≠0时,
②当a+1=0时,
分类讨论思想
这时y是什么函数呢?
一般地,我们把函数y=c(c是常数)叫做
常值函数.它的自变量由所讨论的问题决定.
这是一次函数
即a≠
-1时,
即a=
-1时,
此时函数解析式是
y=
-1,
不是一次函数
已知一个一次函数,当自变量x=2时,
函数值
y=-1;当x=5时,y=8。
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).
例3
解:(1)设所求一次函数的解析式为
y=kx+b(k≠0)
分别把x=2,y=
-1和x=5,y=
8代入解析式,得
-1=2k+b
8=5k+b
解得
所以,这个函数解析式为
待定系数法
要确定k、b,需要两个独立的条件。
已知一个一次函数,当自变量x=2时,
函数值
y=-1;当x=5时,y=8。
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).
例3
解:(1)所以,这个函数解析式为
(2)
课堂练习
课本第3页,练习20.1
/
2,3.
1、一次函数的概念
(1)解析式“形如”__________(k、b是常数,且_______)
(2)定义域是________.
课堂小结
y=kx+b
k≠0
一切实数
2、一次函数与正比例函数的关系
当b=0时,
(k≠0)
3、常值函数的概念
一次函数
正比例函数
一定是
不一定是
4、用待定系数法求一次函数解析式.
函数y=c(c是常数)
设y=kx+b(k≠0)
(k≠0)
★正比例函数的性质
★
解析式形如____________
的函数叫做正比例函数.
★正比例函数
y=kx(k≠0)的图像是经过______
的一条_______
正比例函数
y=kx(k≠0)
原点
y=kx
(k≠0)
大致图像
位置
增减性
k>0
经过第一、三象限
y随x的增大而增大
k<0
经过第二、四象限
y随x的增大而减小
直线
★是不是所有的直线都经过原点呢?
x
y
o
y=kx(k≠0)
是什么函数的图像呢?
第二十章
一次函数
20.1一次函数的概念
思考
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
(1)有人发现,在一定温度下,蟋蟀每分钟鸣叫次数m
与温度
t
(℃)有关,m的值大约是
t
的7倍与35的差。求m与t
的函数解析式
这个函数与正比例函数有何不同?
思考
(2)某城市的本地固定电话的月话费y(元)包括月租费与计时费。月租费为25元,计时费按照每分钟0.1元收取。设小明这个月打了x分钟的电话,求y与x的函数解析式。
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
这个函数与正比例函数有何不同?
思考
(3)一辆汽车行驶在高速公路上,汽车油箱里原有汽油120升,每行驶10千米耗油2升。设汽车行驶的路程为x千米,油箱里剩余的油量为
y升,求y与x的函数解析式。
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
思考
y
=
x
k(常数)
+b(常数)
函数解析式都是关于自变量x的一次整式
写出各问题中的函数解析式,并观察这些解析式有什么共同点?
问:一次函数与正比例函数有什么关系?
新知
一次函数
解析式形如y=kx+b(k、b都是常数,且k≠0)函数叫做一次函数。
一次函数y=kx+b的定义域x取一切实数。
一次函数y=kx+b(k≠0)
则y=kx(k≠0)
正比例函数是一次函数的特例。
当b=0时,
例1
根据变量x、y的关系式,判断y是否是x的一次函数。如果是一次函数,分别指出常数k和b的值。
√
×
√
√
×
×
1、自变量x在分子上(整式)
2、自变量x的指数为1(一次)
例1
根据变量x、y的关系式,判断y是否是x的一次函数。如果是一次函数,分别指出常数k和b的值。
其中哪些是正比例函数?
√
√
√
1、(口答)下列函数中,哪些是一次函数?
课堂练习
课本第3页,练习20.1
/
1.
(4)y=kx+b(k、b是常数).
不是;
是
;
不是;
不是.
k
≠0?
练习:
例2
(1)若
是一次函数,则a满足
的条件是__________
分析:k≠0,即a-2≠0
解得
a≠2
k是什么?
例2
(2)已知变量x、y之间的关系式是
y=(a+1)x+a(其中a是常数)
那么y是x的一次函数吗?
分析:①当a+1≠0时,
②当a+1=0时,
分类讨论思想
这时y是什么函数呢?
一般地,我们把函数y=c(c是常数)叫做
常值函数.它的自变量由所讨论的问题决定.
这是一次函数
即a≠
-1时,
即a=
-1时,
此时函数解析式是
y=
-1,
不是一次函数
已知一个一次函数,当自变量x=2时,
函数值
y=-1;当x=5时,y=8。
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).
例3
解:(1)设所求一次函数的解析式为
y=kx+b(k≠0)
分别把x=2,y=
-1和x=5,y=
8代入解析式,得
-1=2k+b
8=5k+b
解得
所以,这个函数解析式为
待定系数法
要确定k、b,需要两个独立的条件。
已知一个一次函数,当自变量x=2时,
函数值
y=-1;当x=5时,y=8。
(1)求这个函数的解析式;
(2)如果记y=f(x),求f(1).
例3
解:(1)所以,这个函数解析式为
(2)
课堂练习
课本第3页,练习20.1
/
2,3.
1、一次函数的概念
(1)解析式“形如”__________(k、b是常数,且_______)
(2)定义域是________.
课堂小结
y=kx+b
k≠0
一切实数
2、一次函数与正比例函数的关系
当b=0时,
(k≠0)
3、常值函数的概念
一次函数
正比例函数
一定是
不一定是
4、用待定系数法求一次函数解析式.
函数y=c(c是常数)
设y=kx+b(k≠0)
(k≠0)
