沪教版(上海)初中数学七年级第一学期 11.6 轴对称 教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 11.6 轴对称 教案 |
|
|
| 格式 | zip | ||
| 文件大小 | 442.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:32:04 | ||
图片预览

文档简介
11.6
轴
对
称
一、教学目标
1、通过具体实例理解轴对称的意义,掌握轴对称概念.
2、掌握“轴对称图形
”与“两个图形关于一条直线成轴对称”的区别与联系.
3、理解轴对称的性质,会用性质画已知简单图形关于某直线对称的图形,能找到成轴对称的两个图形的对称轴.
二、教学重点、难点
重点:轴对称的概念
难点:轴对称和轴对称图形的区别与联系
3、
教学过程
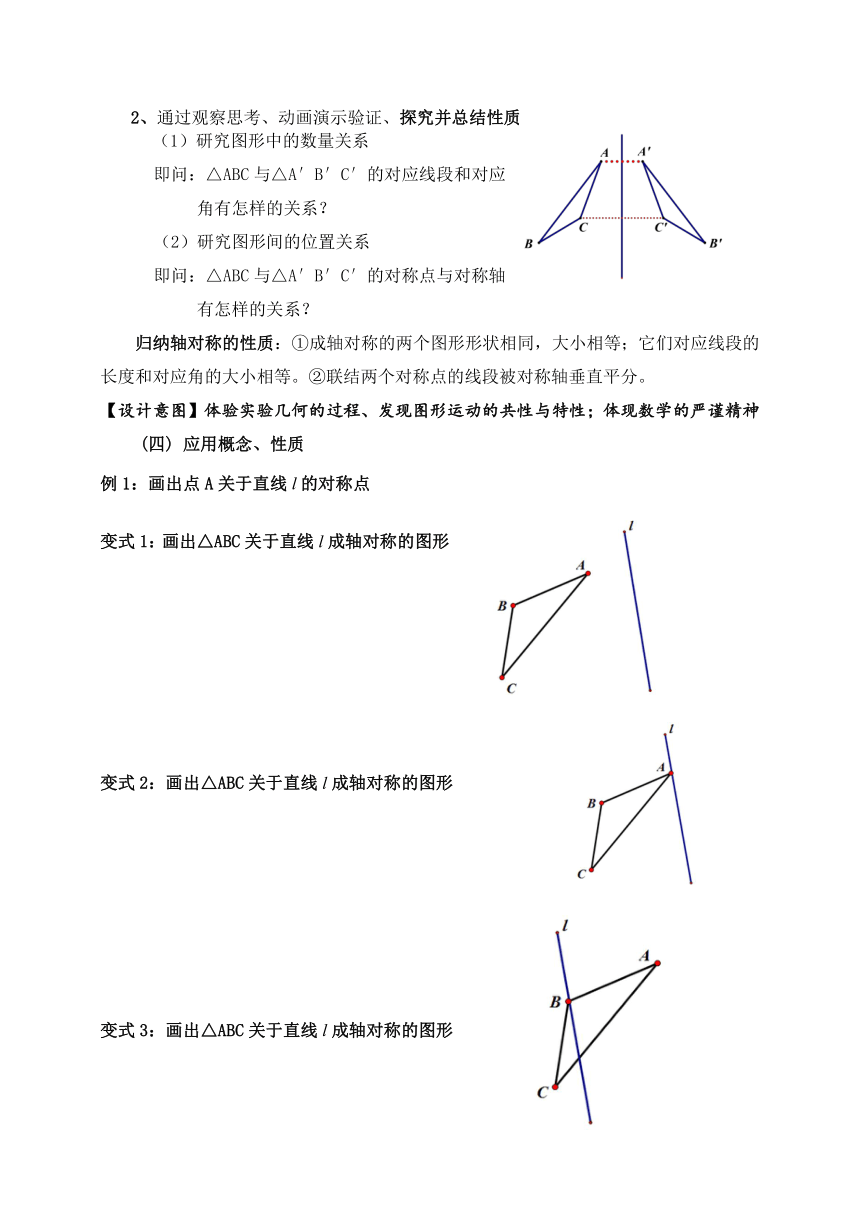
(一)复习旧知:通过识图复习轴对称图形概念.
(二)引出概念:观察思考,对比上下两组图形,发现它们的区别和联系,引出轴对称概念
【设计意图】从生活到数学,复杂到简洁;对比图形异同,引出概念
(三)形成概念、总结性质
1、通过观察思考、类比的方式,归纳轴对称定义:
如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点。
2、通过观察思考、动画演示验证、探究并总结性质
(1)研究图形中的数量关系
即问:△ABC与△A′B′C′的对应线段和对应角有怎样的关系?
(2)研究图形间的位置关系
即问:△ABC与△A′B′C′的对称点与对称轴有怎样的关系?
归纳轴对称的性质:①成轴对称的两个图形形状相同,大小相等;它们对应线段的长度和对应角的大小相等。②联结两个对称点的线段被对称轴垂直平分。
【设计意图】体验实验几何的过程、发现图形运动的共性与特性;体现数学的严谨精神
(四)
应用概念、性质
例1:画出点A关于直线l的对称点
变式1:画出△ABC关于直线l成轴对称的图形
变式2:画出△ABC关于直线l成轴对称的图形
变式3:画出△ABC关于直线l成轴对称的图形
例2、思考与作图:图中两个四边形关于直线l成轴对称,画出它们的对称轴l,并总结方法.
3、变式与提升
作图:若四边形ABCD与四边形A′B′C′D′关于直线l成轴对称,已知点A的对称点为点A′,请画出四边形A′B′C′D′。
(五)轴对称图形和轴对称的区别和联系
(六)课堂小结
1、知识点小结:
2、思想方法小结:
(七)
作业
1、课本P109;
2、练习册11.6;
3、拓展:(1)如图是由16个小正方形构成的大正方形,求∠1+∠2+∠3+∠4+∠5+∠6+∠7等于多少度?
(2)已知四边形ABCD,如果点D、C关于直线MN对称,画出直线MN;画出四边形ABCD关于直线MN的对称图形.
(3)已知:A、B两个工厂在铁路L的同侧,要在铁路边建一个货场C,货场应建在什么地方,才能使A、B两厂到货场C的距离之和最短。
??
轴
对
称
一、教学目标
1、通过具体实例理解轴对称的意义,掌握轴对称概念.
2、掌握“轴对称图形
”与“两个图形关于一条直线成轴对称”的区别与联系.
3、理解轴对称的性质,会用性质画已知简单图形关于某直线对称的图形,能找到成轴对称的两个图形的对称轴.
二、教学重点、难点
重点:轴对称的概念
难点:轴对称和轴对称图形的区别与联系
3、
教学过程
(一)复习旧知:通过识图复习轴对称图形概念.
(二)引出概念:观察思考,对比上下两组图形,发现它们的区别和联系,引出轴对称概念
【设计意图】从生活到数学,复杂到简洁;对比图形异同,引出概念
(三)形成概念、总结性质
1、通过观察思考、类比的方式,归纳轴对称定义:
如果把一个图形沿某一条直线翻折,能与另一个图形重合,那么叫做这两个图形关于这条直线成轴对称,这条直线叫做对称轴,两个图形中的对应点叫做关于这条直线的对称点。
2、通过观察思考、动画演示验证、探究并总结性质
(1)研究图形中的数量关系
即问:△ABC与△A′B′C′的对应线段和对应角有怎样的关系?
(2)研究图形间的位置关系
即问:△ABC与△A′B′C′的对称点与对称轴有怎样的关系?
归纳轴对称的性质:①成轴对称的两个图形形状相同,大小相等;它们对应线段的长度和对应角的大小相等。②联结两个对称点的线段被对称轴垂直平分。
【设计意图】体验实验几何的过程、发现图形运动的共性与特性;体现数学的严谨精神
(四)
应用概念、性质
例1:画出点A关于直线l的对称点
变式1:画出△ABC关于直线l成轴对称的图形
变式2:画出△ABC关于直线l成轴对称的图形
变式3:画出△ABC关于直线l成轴对称的图形
例2、思考与作图:图中两个四边形关于直线l成轴对称,画出它们的对称轴l,并总结方法.
3、变式与提升
作图:若四边形ABCD与四边形A′B′C′D′关于直线l成轴对称,已知点A的对称点为点A′,请画出四边形A′B′C′D′。
(五)轴对称图形和轴对称的区别和联系
(六)课堂小结
1、知识点小结:
2、思想方法小结:
(七)
作业
1、课本P109;
2、练习册11.6;
3、拓展:(1)如图是由16个小正方形构成的大正方形,求∠1+∠2+∠3+∠4+∠5+∠6+∠7等于多少度?
(2)已知四边形ABCD,如果点D、C关于直线MN对称,画出直线MN;画出四边形ABCD关于直线MN的对称图形.
(3)已知:A、B两个工厂在铁路L的同侧,要在铁路边建一个货场C,货场应建在什么地方,才能使A、B两厂到货场C的距离之和最短。
??
