北师大版八年级数学下册课件: 1.1 第4课时 等边三角形的判定和含30°角的直角三角形(共20张ppt)
文档属性
| 名称 | 北师大版八年级数学下册课件: 1.1 第4课时 等边三角形的判定和含30°角的直角三角形(共20张ppt) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 22:14:08 | ||
图片预览




文档简介
第一章 三角形的证明
1 第4课时
等边三角形的判定和含30°角的直角三角形
知识回顾
等边三角形的性质:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,并且每个角都等于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长度相等.
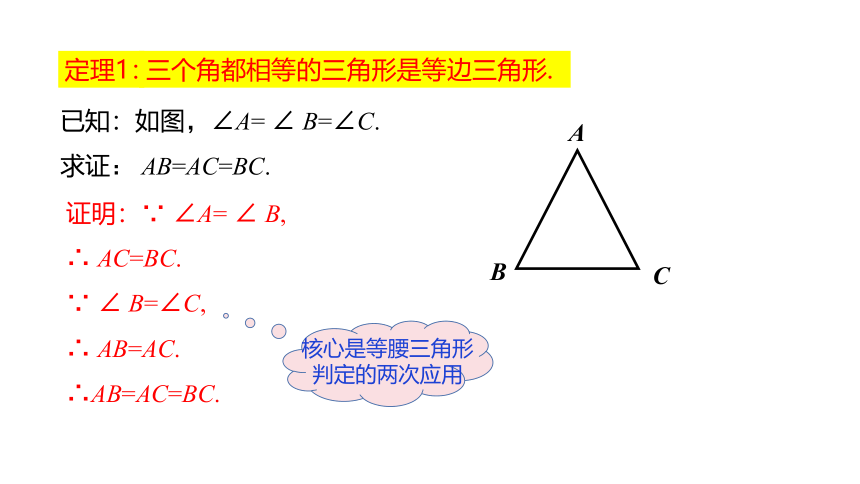
定理 三个角都相等的三角形是等边三角形.
定理 有一个角等于60°的等腰三角形是等边三角形.
你能证明这些定理吗?
获取新知
知识点一:等边三角形的判定
一个三角形满足什么条件时是等边三角形? 一个等腰三角形满足什么条件时是等边三角形?请证明自己的结论,并与同伴交流.
核心是等腰三角形判定的两次应用
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
证明:∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
A
B
C
三个角都相等的三角形是等边三角形.
定理1:
等腰三角形的性质+内角和定理=定理1
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
定理2:有一个角是60°的等腰三角形是等边三角形.
证明完整吗?是不是还有另一种情形呢?
例题讲解
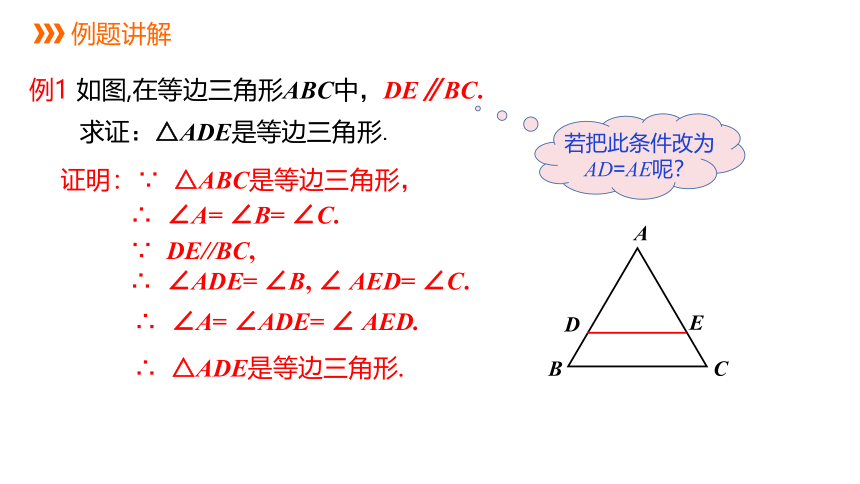
例1 如图,在等边三角形ABC中,DE∥BC.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
A
C
B
D
E
若把此条件改为AD=AE呢?
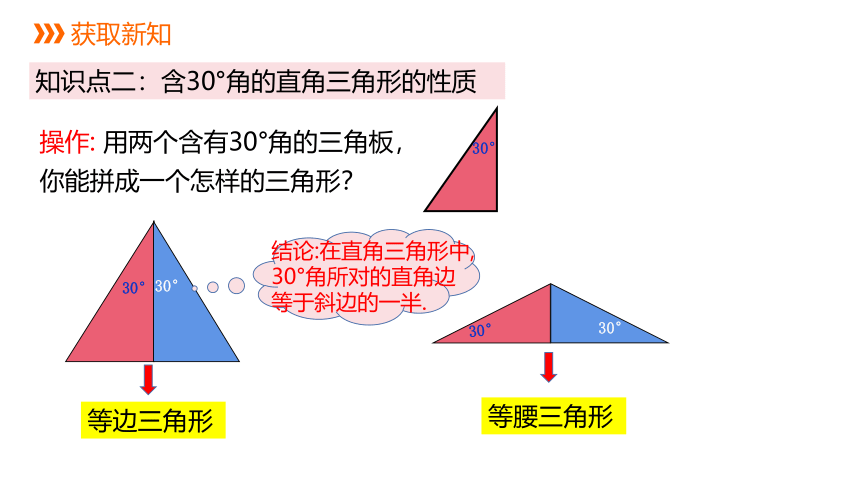
知识点二:含30°角的直角三角形的性质
获取新知
操作: 用两个含有30°角的三角板,你能拼成一个怎样的三角形?
30°
30°
30°
30°
30°
等边三角形
等腰三角形
结论:在直角三角形中, 30°角所对的直角边等于斜边的一半.
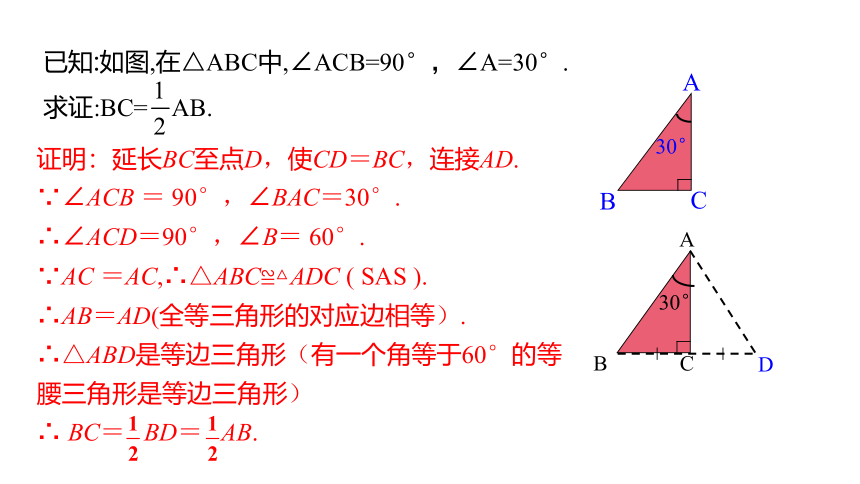
已知:如图,在△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
A
30°
B
C
证明:延长BC至点D,使CD=BC,连接AD.
∵∠ACB = 90°,∠BAC=30°.
∴∠ACD=90°,∠B= 60°.
∵AC =AC,∴△ABC≌△ADC ( SAS ).
∴AB=AD(全等三角形的对应边相等).
∴△ABD是等边三角形(有一个角等于60°的等
腰三角形是等边三角形)
∴ BC= BD= AB.
30°
A
B
C
D
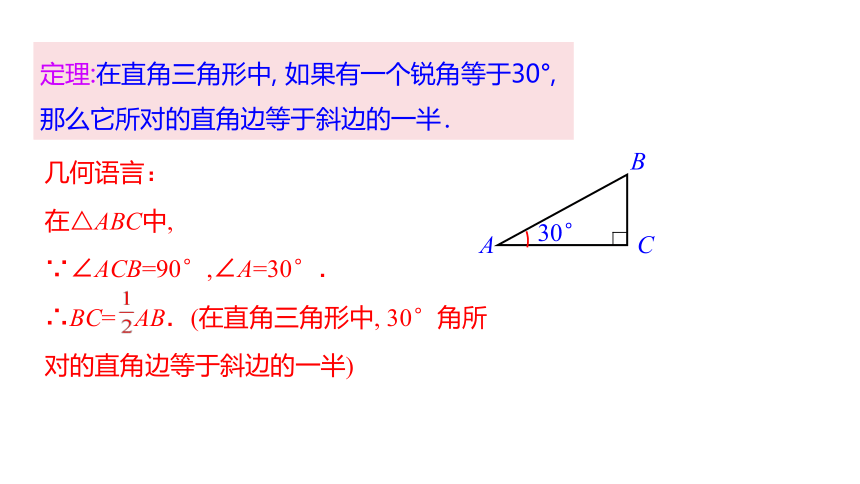
定理:在直角三角形中, 如果有一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
几何语言:
在△ABC中,
∵∠ACB=90°,∠A=30°.
∴BC= AB.(在直角三角形中, 30°角所对的直角边等于斜边的一半)
A
B
C
30°
例题讲解
例2 求证:如果等腰三角形的底角为15°,
那么腰上的高是腰长的一半.
已知:如图,在△ABC中,AB = AC, ∠B=15°,
CD是腰AB上的高.
求证:CD= AB
C
B
A
D
证明:在△ABC中,
∵AB=AC,∠B=15°
∴∠ACB=∠B=15°(等边对等角).
∴∠DAC=∠B+∠ACB=15°+15°=30°.
∴CD是腰AB上的高,
∴∠ADC= 90°.
∴CD= AC(在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半).
∴CD = AB.
C
B
A
D
随堂演练
1. 等腰三角形补充下列条件后,仍不一定成为等边三角形的是( )
A.有一个内角是60°
B.有一个外角是120°
C.有两个角相等
D.腰与底边相等
C
2. 如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个
B.3个
C.4个
D.5个
D
3.如图,已知在△ABC中,AB=AC,∠C=30°,
AB⊥AD,则下列关系式正确的为( )
A.BD=CD B.BD=2CD
C.BD=3CD D.BD=4CD
B
4.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图①,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图②,则此时A,B两点之间的距离是 cm.
18
5.如图,在△ABC中,∠B=90°,∠C=30°,AB=3,
则AC=____,BC=______.
6
A
B
C
3
30°
6.如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD.求证:△OCD是等边三角形.
证明:∵OA=OB,∠A=60°, ∴∠B=∠A=60°.
又∵AB∥CD,
∴∠C=∠A=60°,∠D=∠B=60°, ∴∠COD=∠D=∠C=60°, ∴△OCD是等边三角形.
7.已知:在Rt△ABC中,∠C=90°, BC= AB.
求证:∠BAC=30°.
C
B
A
证明:延长BC至D,使CD=BC,连接AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC,
∴△ACB≌△ACD(SAS).
∴AB=AD.
∵CD=BC,∴BC= BD.
又∵BC= AB,∴AB=BD.
∴AB=AD=BD,
即△ABD是等边三角形.
∴∠B=60°.在Rt△ABC中,∠BAC=30°.
C
B
A
D
课堂小结
等边三角形的判定方法:
(2) 含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对
的直角边等于斜边的一半.
+底和腰相等
+有一个角是60°
等腰三角形 等边三角形
三个角相等
三角形 等边三角形
1 第4课时
等边三角形的判定和含30°角的直角三角形
知识回顾
等边三角形的性质:
(1)等边三角形的三边都相等;
(2)等边三角形的三个内角都相等,并且每个角都等于60°;
(3)等边三角形是轴对称图形,它有三条对称轴,分别为三边的垂直平分线;
(4)各边上的高、中线、对应的角平分线重合,且长度相等.
定理 三个角都相等的三角形是等边三角形.
定理 有一个角等于60°的等腰三角形是等边三角形.
你能证明这些定理吗?
获取新知
知识点一:等边三角形的判定
一个三角形满足什么条件时是等边三角形? 一个等腰三角形满足什么条件时是等边三角形?请证明自己的结论,并与同伴交流.
核心是等腰三角形判定的两次应用
已知:如图,∠A= ∠ B=∠C.
求证: AB=AC=BC.
证明:∵ ∠A= ∠ B,
∴ AC=BC.
∵ ∠ B=∠C,
∴ AB=AC.
∴AB=AC=BC.
A
B
C
三个角都相等的三角形是等边三角形.
定理1:
等腰三角形的性质+内角和定理=定理1
已知: 若AB=AC , ∠A= 60°.
求证: AB=AC=BC.
证明:∵AB=AC , ∠A= 60 °.
∴∠B=∠C= (180。-∠A)= 60°.
∴∠A= ∠ B=∠C.
∴AB=AC=BC.
定理2:有一个角是60°的等腰三角形是等边三角形.
证明完整吗?是不是还有另一种情形呢?
例题讲解
例1 如图,在等边三角形ABC中,DE∥BC.
求证:△ADE是等边三角形.
证明:∵ △ABC是等边三角形,
∴ ∠A= ∠B= ∠C.
∵ DE//BC,
∴ ∠ADE= ∠B, ∠ AED= ∠C.
∴ ∠A= ∠ADE= ∠ AED.
∴ △ADE是等边三角形.
A
C
B
D
E
若把此条件改为AD=AE呢?
知识点二:含30°角的直角三角形的性质
获取新知
操作: 用两个含有30°角的三角板,你能拼成一个怎样的三角形?
30°
30°
30°
30°
30°
等边三角形
等腰三角形
结论:在直角三角形中, 30°角所对的直角边等于斜边的一半.
已知:如图,在△ABC中,∠ACB=90°,∠A=30°.
求证:BC= AB.
A
30°
B
C
证明:延长BC至点D,使CD=BC,连接AD.
∵∠ACB = 90°,∠BAC=30°.
∴∠ACD=90°,∠B= 60°.
∵AC =AC,∴△ABC≌△ADC ( SAS ).
∴AB=AD(全等三角形的对应边相等).
∴△ABD是等边三角形(有一个角等于60°的等
腰三角形是等边三角形)
∴ BC= BD= AB.
30°
A
B
C
D
定理:在直角三角形中, 如果有一个锐角等于30°,
那么它所对的直角边等于斜边的一半.
几何语言:
在△ABC中,
∵∠ACB=90°,∠A=30°.
∴BC= AB.(在直角三角形中, 30°角所对的直角边等于斜边的一半)
A
B
C
30°
例题讲解
例2 求证:如果等腰三角形的底角为15°,
那么腰上的高是腰长的一半.
已知:如图,在△ABC中,AB = AC, ∠B=15°,
CD是腰AB上的高.
求证:CD= AB
C
B
A
D
证明:在△ABC中,
∵AB=AC,∠B=15°
∴∠ACB=∠B=15°(等边对等角).
∴∠DAC=∠B+∠ACB=15°+15°=30°.
∴CD是腰AB上的高,
∴∠ADC= 90°.
∴CD= AC(在直角三角形中,如果一个锐角等于30°,
那么它所对的直角边等于斜边的一半).
∴CD = AB.
C
B
A
D
随堂演练
1. 等腰三角形补充下列条件后,仍不一定成为等边三角形的是( )
A.有一个内角是60°
B.有一个外角是120°
C.有两个角相等
D.腰与底边相等
C
2. 如图,△ABC是等边三角形,D,E,F为各边中点,则图中共有等边三角形( )
A.2个
B.3个
C.4个
D.5个
D
3.如图,已知在△ABC中,AB=AC,∠C=30°,
AB⊥AD,则下列关系式正确的为( )
A.BD=CD B.BD=2CD
C.BD=3CD D.BD=4CD
B
4.由于木质衣架没有柔性,在挂置衣服的时候不太方便操作.小敏设计了一种衣架,在使用时能轻易收拢,然后套进衣服后松开即可.如图①,衣架杆OA=OB=18 cm,若衣架收拢时,∠AOB=60°,如图②,则此时A,B两点之间的距离是 cm.
18
5.如图,在△ABC中,∠B=90°,∠C=30°,AB=3,
则AC=____,BC=______.
6
A
B
C
3
30°
6.如图,AC与BD相交于点O,若OA=OB,∠A=60°,且AB∥CD.求证:△OCD是等边三角形.
证明:∵OA=OB,∠A=60°, ∴∠B=∠A=60°.
又∵AB∥CD,
∴∠C=∠A=60°,∠D=∠B=60°, ∴∠COD=∠D=∠C=60°, ∴△OCD是等边三角形.
7.已知:在Rt△ABC中,∠C=90°, BC= AB.
求证:∠BAC=30°.
C
B
A
证明:延长BC至D,使CD=BC,连接AD.
∵∠ACB=90°,∴∠ACD=90°.
又∵AC=AC,
∴△ACB≌△ACD(SAS).
∴AB=AD.
∵CD=BC,∴BC= BD.
又∵BC= AB,∴AB=BD.
∴AB=AD=BD,
即△ABD是等边三角形.
∴∠B=60°.在Rt△ABC中,∠BAC=30°.
C
B
A
D
课堂小结
等边三角形的判定方法:
(2) 含30°角的直角三角形的性质:
在直角三角形中,如果一个锐角等于30°,那么它所对
的直角边等于斜边的一半.
+底和腰相等
+有一个角是60°
等腰三角形 等边三角形
三个角相等
三角形 等边三角形
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
