北师大版九年级下册 1.5三角函数的应用(共36张ppt)
文档属性
| 名称 | 北师大版九年级下册 1.5三角函数的应用(共36张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 22:24:01 | ||
图片预览



文档简介
第四节 三角函数的应用(1)
第一章: 直角三角形的边角关系
学习目标:(1分钟)
2.掌握三角函数2种基本图形的应用
1.掌握方位角, 仰角, 俯角的概念
3.列方程求解应用题
70?
O
A
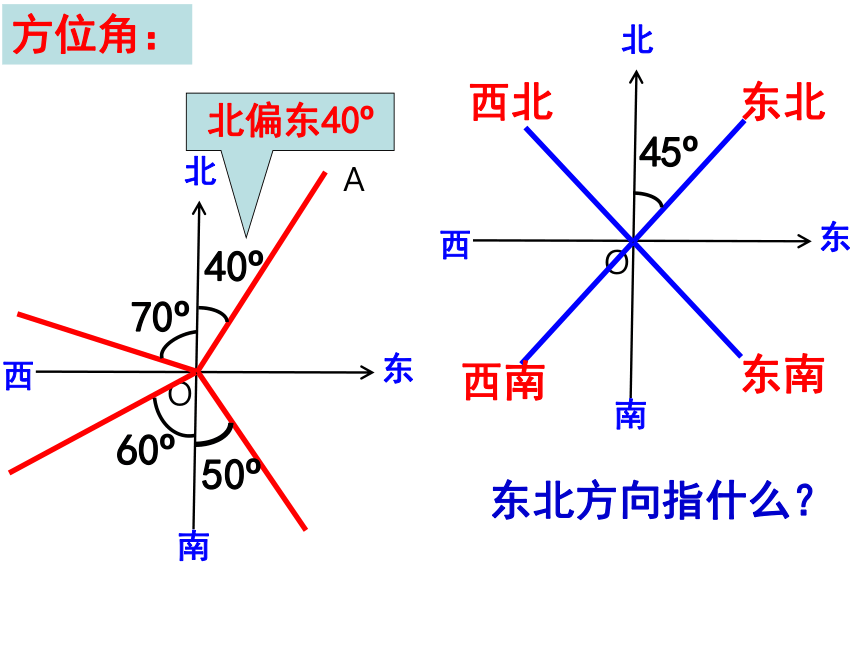
东北方向指什么?
方位角:
北
南
西
东
40?
北偏东40?
50?
60?
O
北
南
西
东
45?
东北
西南
西北
东南
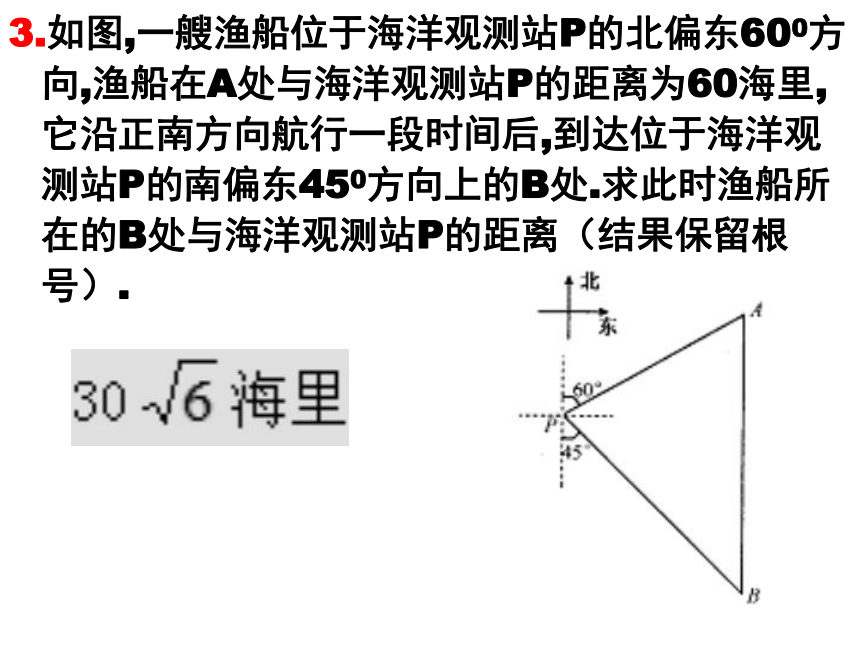
3.如图,一艘渔船位于海洋观测站P的北偏东600方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东450方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
导学提示:
1.从数学的角度分析,本题的已知量是什么?在图形中是如何体现的?
2.你是如何理解船有没有触礁的危险?本题实际上是求解哪个量?
3.运用哪个基本模型求解?
自学指导1:(4分钟)
结合下面的导学提示,完成课本P19想一想之前的问题.
A
B
C
北
东
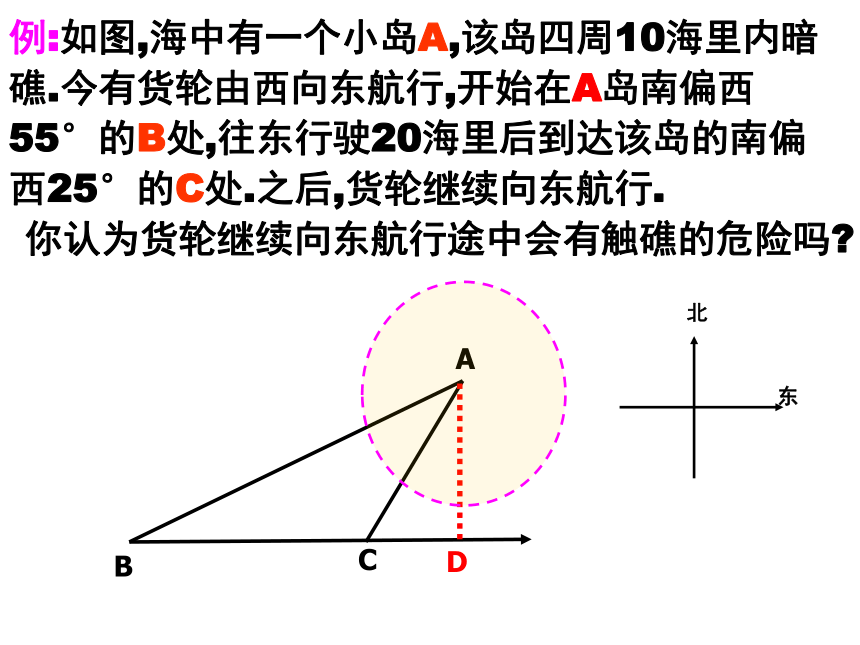
例:如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
D
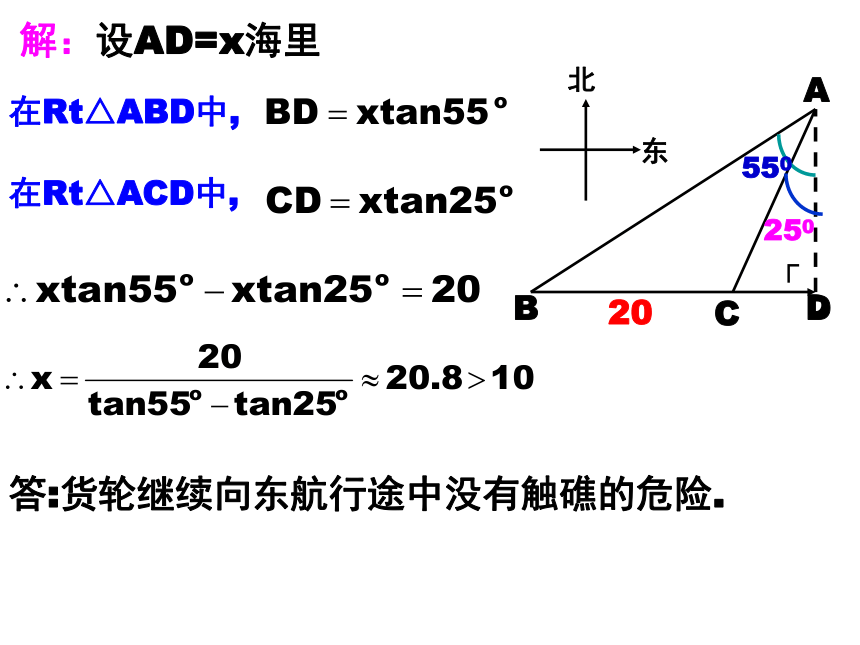
解:设AD=x海里
答:货轮继续向东航行途中没有触礁的危险.
在Rt△ABD中,
在Rt△ACD中,
D
┌
A
B
C
D
北
东
550
250
20
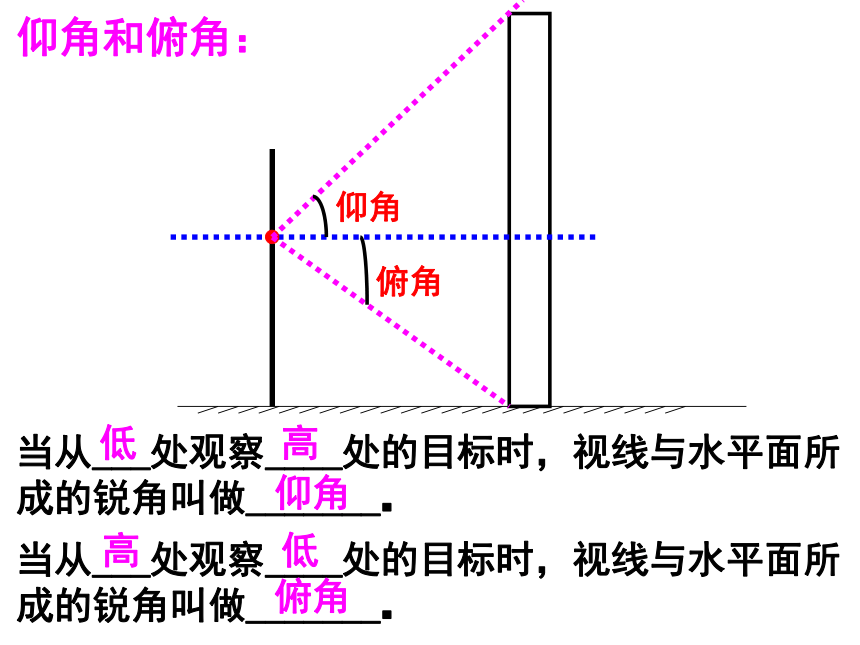
仰角和俯角:
仰角
俯角
当从___处观察____处的目标时,视线与水平面所成的锐角叫做_______.
仰角
当从___处观察____处的目标时,视线与水平面所成的锐角叫做_______.
俯角
低
高
高
低
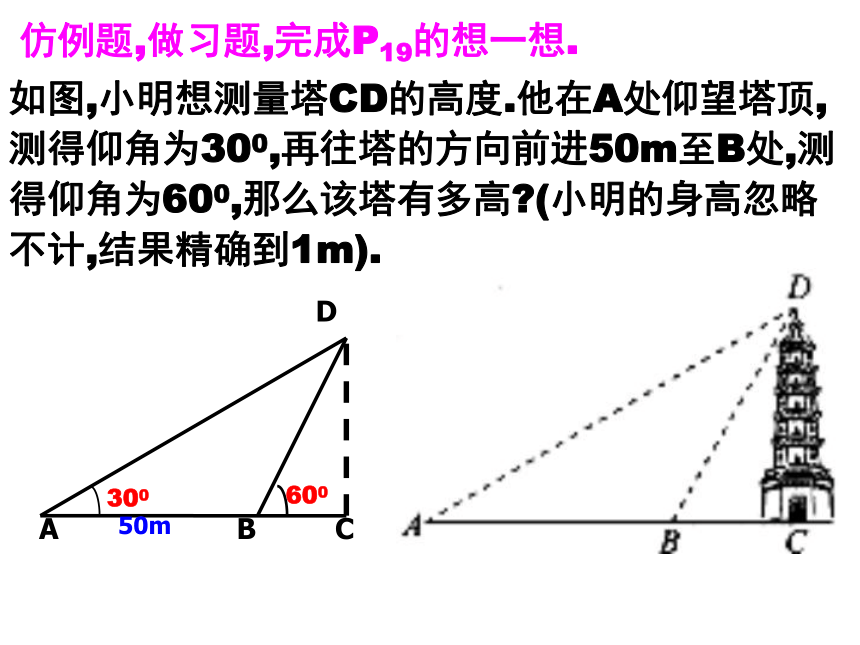
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
仿例题,做习题,完成P19的想一想.
D
A
B
C
50m
300
600
D
A
B
C
50m
300
600
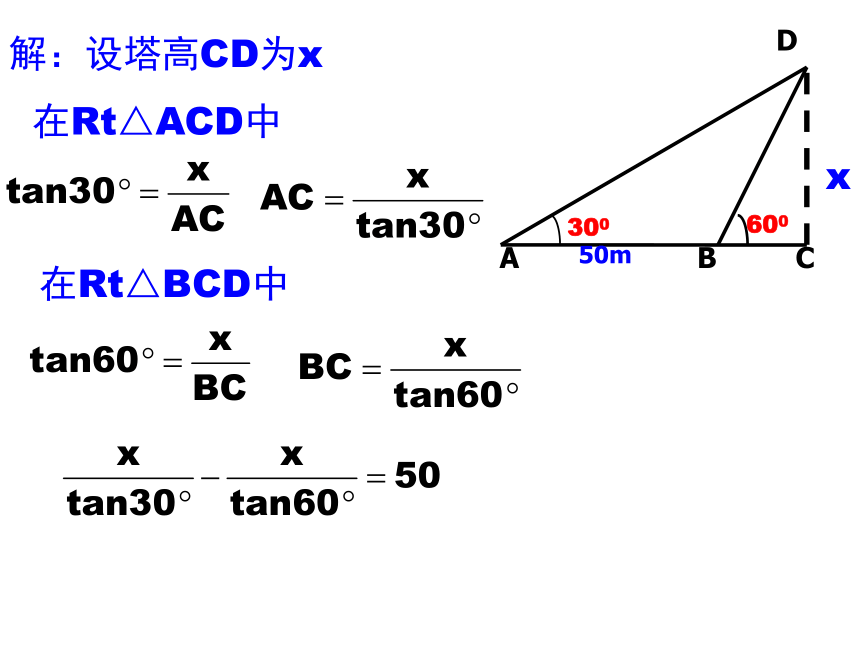
解:设塔高CD为x
在Rt△ACD中
x
在Rt△BCD中
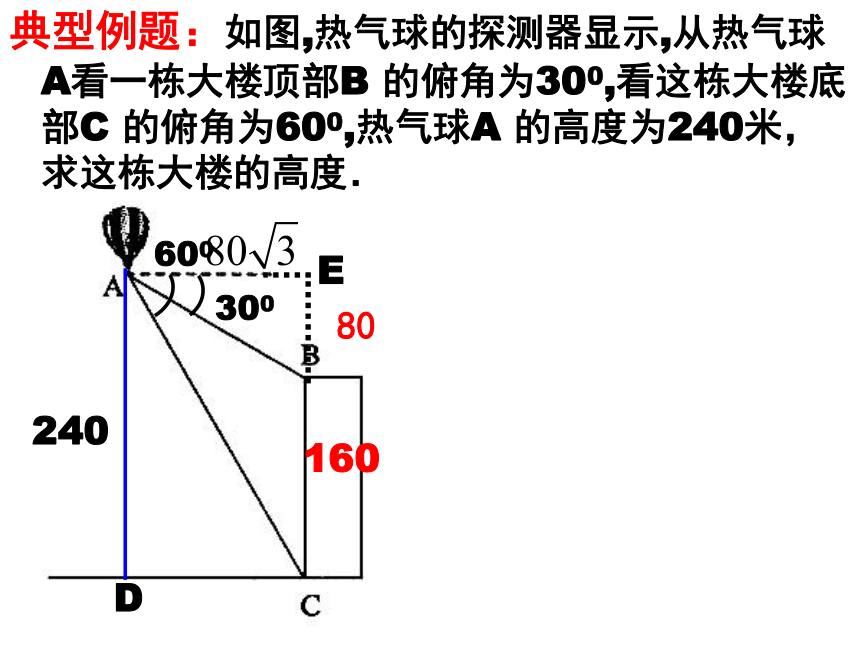
典型例题:如图,热气球的探测器显示,从热气球A看一栋大楼顶部B 的俯角为300,看这栋大楼底部C 的俯角为600,热气球A 的高度为240米,求这栋大楼的高度.
300
600
D
240
E
80
160
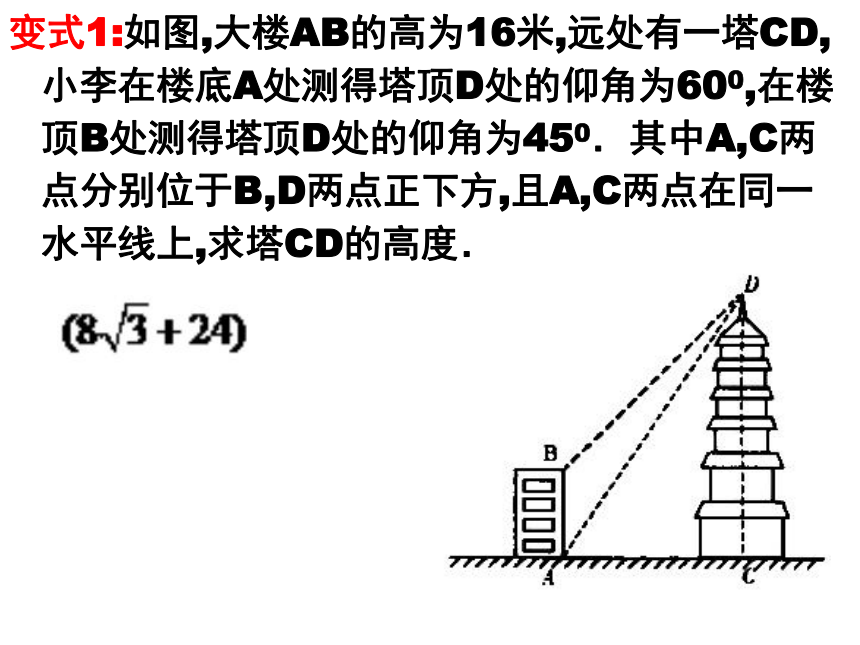
变式1:如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为600,在楼顶B处测得塔顶D处的仰角为450.其中A,C两点分别位于B,D两点正下方,且A,C两点在同一水平线上,求塔CD的高度.
自学检测:(8分钟)
做一做:某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,
(1)调整后的楼梯会加长多少?
(2)楼梯多占多长一段地面?(结果精确到0.01m).
A
B
C
D
┌
AB-BD的长
AD的长
解:(1)如图,由题知,
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
在Rt△BCD中
在Rt△ABC中
解:
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
在Rt△BCD中
在Rt△ABC中
习题1.6-4T:一艘货轮以36海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续航行40min后到达C处,发现灯塔B在它北偏东75°方向,求此时货轮与灯塔B的距离(结果精确到0.01海里)
45°
75°
随堂练习-1T:如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
E
B
C
D
2m
400
5m
随堂练习-2T如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m,坡底BC=30m,
∠ADC=135°,
(1)求∠ABC的大小
(2)如果坝长100m,那么建筑这个大坝共需多少石料?(结果精确到0.01m3)
变式.水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
小结:(1分钟)
题型1:花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为350时,问:
(1)商场以上的居民住房采光是否有影响,为什么?
(2)若要使商场采光不受影响,两楼应相距多少米?
(结果保留一位小数)参考数据:sin350≈0.57,cos350≈0.82,tan350≈0.70)
保留两位数字
同类变式:某居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为290.(1)中午时,超市以上的居民住房采光是否有影响,为什么?(2)若要使得超市采光不受影响,两楼应至少相距多少米?(结果保留整数)
1.A,B两市相距150千米,分别从A,B 处测得国家级风景区中心C 处的方位角如图所示,风景区区域是以C 为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部分设计修建连接A,B两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
CD=50>45
D
A
B
C
∟
当堂训练:
2.(台风问题).台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
(1)该城市是否会受到这次台风的影响?为什么?
(1)如图,由点A作AD⊥BC,垂足为D
∵AB=220千米,∠B=30°
∴AD=110千米
∵110千米<160千米
∴该城市会受到这次台风的影响。
D
300
220
∟
110
(2)若受到台风影响,那么台风影响该城市的持续时间有多长?
D
解(2)令AE=AF=160千米,当台风中心从E处移动到F处时,该城市都会受到这次台风的影响,由勾股定理得:
E
F
ED=
∴EF= (千米)
∴台风影响该城市的持续时间为
110
160
∟
解:(3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为
(3)该城市受到台风影响的最大风力为几级?
D
110
∟
3.如图,铁路MN和铁路PQ在P点处交汇,点A处是学校, AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响.
(1)火车在铁路MN上沿PN方向行驶时,学校是否会受到影响?请说明理由.
(2)如果受到影响,已知火车的速度是180千米/时那么学校受到影响的时间是多久?
噪音问题
(1)会受到影响.
过点A作AE⊥MN于点E,
∵点A到铁路MN的距离为80米,∴AE=80m,
∵周围100米以内会受到噪音影响,
80<100,∴学校会受到影响;
E
∟
(2)以点A为圆心,100米为半径画圆,交直线MN于BC两点,连接AB、AC,则AB=AC=100m,在Rt△ABE中,∵AB=100m,AE=80m∴BE=60m,
∴BC=2BE=120m,
∵火车的速度是180千米/时=50m/s,
∴t=BC/50=120/50=2.4s.
答:学校受到影响的时间是2.4秒.
B
C
E
4.如图,MN表示某引水工程的一段设计路线,在M的北偏东60°的方向上有一点A,以A为中心周围600米范围内为居民区,取MN上另一点B,测得BA的方向为北偏东45°已知MB=400m
①如果不改变方向,那么输水路线是否会穿过居民区?
北
北
A
60°
45°
M
B
N
东
H
②若输水路线穿过居民区,求输水路线落在居民区内部分的长度(精确到1米)。
北
北
A
60°
45°
M
B
N
东
H
E
F
③为避免输水路线穿过居民区,在M点应怎样适当地调整输水线路的走向?
(偏转角度精确到1分)
北
北
A
60°
45°
M
B
N
东
G
(变式)如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风正以40海里/时的速度由A向北偏西60°方向移动.距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否受到台风的影响?请说明理由.
A
B
C
北
60°
320
160
●
∟
30°
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?
A
C
60°
D
320
160
200
120
●
B
∟
30°
中考链接:1.如图,AC是普宁市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东450方向、点B的北偏东300方向上,AB=2km,∠DAC=150.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
第一章: 直角三角形的边角关系
学习目标:(1分钟)
2.掌握三角函数2种基本图形的应用
1.掌握方位角, 仰角, 俯角的概念
3.列方程求解应用题
70?
O
A
东北方向指什么?
方位角:
北
南
西
东
40?
北偏东40?
50?
60?
O
北
南
西
东
45?
东北
西南
西北
东南
3.如图,一艘渔船位于海洋观测站P的北偏东600方向,渔船在A处与海洋观测站P的距离为60海里,它沿正南方向航行一段时间后,到达位于海洋观测站P的南偏东450方向上的B处.求此时渔船所在的B处与海洋观测站P的距离(结果保留根号).
导学提示:
1.从数学的角度分析,本题的已知量是什么?在图形中是如何体现的?
2.你是如何理解船有没有触礁的危险?本题实际上是求解哪个量?
3.运用哪个基本模型求解?
自学指导1:(4分钟)
结合下面的导学提示,完成课本P19想一想之前的问题.
A
B
C
北
东
例:如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
D
解:设AD=x海里
答:货轮继续向东航行途中没有触礁的危险.
在Rt△ABD中,
在Rt△ACD中,
D
┌
A
B
C
D
北
东
550
250
20
仰角和俯角:
仰角
俯角
当从___处观察____处的目标时,视线与水平面所成的锐角叫做_______.
仰角
当从___处观察____处的目标时,视线与水平面所成的锐角叫做_______.
俯角
低
高
高
低
如图,小明想测量塔CD的高度.他在A处仰望塔顶,测得仰角为300,再往塔的方向前进50m至B处,测得仰角为600,那么该塔有多高?(小明的身高忽略不计,结果精确到1m).
仿例题,做习题,完成P19的想一想.
D
A
B
C
50m
300
600
D
A
B
C
50m
300
600
解:设塔高CD为x
在Rt△ACD中
x
在Rt△BCD中
典型例题:如图,热气球的探测器显示,从热气球A看一栋大楼顶部B 的俯角为300,看这栋大楼底部C 的俯角为600,热气球A 的高度为240米,求这栋大楼的高度.
300
600
D
240
E
80
160
变式1:如图,大楼AB的高为16米,远处有一塔CD,小李在楼底A处测得塔顶D处的仰角为600,在楼顶B处测得塔顶D处的仰角为450.其中A,C两点分别位于B,D两点正下方,且A,C两点在同一水平线上,求塔CD的高度.
自学检测:(8分钟)
做一做:某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,
(1)调整后的楼梯会加长多少?
(2)楼梯多占多长一段地面?(结果精确到0.01m).
A
B
C
D
┌
AB-BD的长
AD的长
解:(1)如图,由题知,
A
B
C
D
┌
4m
350
400
答:调整后的楼梯会加长约0.48m.
在Rt△BCD中
在Rt△ABC中
解:
A
B
C
D
┌
4m
350
400
答:楼梯多占约0.61m一段地面.
在Rt△BCD中
在Rt△ABC中
习题1.6-4T:一艘货轮以36海里/时的速度在海面上航行,当它行驶到A处时,发现它的东北方向有一灯塔B,货轮继续航行40min后到达C处,发现灯塔B在它北偏东75°方向,求此时货轮与灯塔B的距离(结果精确到0.01海里)
45°
75°
随堂练习-1T:如图,一灯柱AB被一钢缆CD固定.CD与地面成400夹角,且DB=5m.现再在CD上方2m处加固另一根钢缆ED,那么,钢缆ED的长度为多少?(结果精确到0.01m).
E
B
C
D
2m
400
5m
随堂练习-2T如图,水库大坝的截面是梯形ABCD,坝顶AD=6m,坡长CD=8m,坡底BC=30m,
∠ADC=135°,
(1)求∠ABC的大小
(2)如果坝长100m,那么建筑这个大坝共需多少石料?(结果精确到0.01m3)
变式.水利部门为加强防汛工作,决定对某水库大坝进行加固,大坝的横截面是梯形ABCD.如图所示,已知迎水坡面AB的长为16米,∠B=60°,背水坡面CD的长为16 米,加固后大坝的横截面积为梯形ABED,CE的长为8米.
(1)已知需加固的大坝长为150米,求需要填土石方多少立方米?
(2)求加固后的大坝背水坡面DE的坡度.
小结:(1分钟)
题型1:花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为350时,问:
(1)商场以上的居民住房采光是否有影响,为什么?
(2)若要使商场采光不受影响,两楼应相距多少米?
(结果保留一位小数)参考数据:sin350≈0.57,cos350≈0.82,tan350≈0.70)
保留两位数字
同类变式:某居民楼的一楼是高6米的小区超市,超市以上是居民住房.在该楼前面15米处要盖一栋高20米的新楼.已知上海地区冬至正午的阳光与水平线夹角为290.(1)中午时,超市以上的居民住房采光是否有影响,为什么?(2)若要使得超市采光不受影响,两楼应至少相距多少米?(结果保留整数)
1.A,B两市相距150千米,分别从A,B 处测得国家级风景区中心C 处的方位角如图所示,风景区区域是以C 为圆心,45千米为半径的圆,tanα=1.627,tanβ=1.373.为了开发旅游,有关部分设计修建连接A,B两市的高速公路.问连接AB高速公路是否穿过风景区,请说明理由.
CD=50>45
D
A
B
C
∟
当堂训练:
2.(台风问题).台风是一种自然灾害,它以台风中心为圆心在数十千米范围内形成气旋风暴,有极强的破坏力,据气象观察,距沿海某城市A正南220千米的B处有一台风中心,其中心最大风力为12级,每远离台风中心20千米,风力就会减弱一级,该台风中心正以15千米/时的速度沿北偏东30°方向向C移动,且台风中心风力不变,若城市受到的风力达到或超过四级,则称受台风影响.
(1)该城市是否会受到这次台风的影响?为什么?
(1)如图,由点A作AD⊥BC,垂足为D
∵AB=220千米,∠B=30°
∴AD=110千米
∵110千米<160千米
∴该城市会受到这次台风的影响。
D
300
220
∟
110
(2)若受到台风影响,那么台风影响该城市的持续时间有多长?
D
解(2)令AE=AF=160千米,当台风中心从E处移动到F处时,该城市都会受到这次台风的影响,由勾股定理得:
E
F
ED=
∴EF= (千米)
∴台风影响该城市的持续时间为
110
160
∟
解:(3)当台风中心位于D处时,A市所受这次台风的风力最大,其最大风力为
(3)该城市受到台风影响的最大风力为几级?
D
110
∟
3.如图,铁路MN和铁路PQ在P点处交汇,点A处是学校, AP=160米,点A到铁路MN的距离为80米,假使火车行驶时,周围100米以内会受到噪音影响.
(1)火车在铁路MN上沿PN方向行驶时,学校是否会受到影响?请说明理由.
(2)如果受到影响,已知火车的速度是180千米/时那么学校受到影响的时间是多久?
噪音问题
(1)会受到影响.
过点A作AE⊥MN于点E,
∵点A到铁路MN的距离为80米,∴AE=80m,
∵周围100米以内会受到噪音影响,
80<100,∴学校会受到影响;
E
∟
(2)以点A为圆心,100米为半径画圆,交直线MN于BC两点,连接AB、AC,则AB=AC=100m,在Rt△ABE中,∵AB=100m,AE=80m∴BE=60m,
∴BC=2BE=120m,
∵火车的速度是180千米/时=50m/s,
∴t=BC/50=120/50=2.4s.
答:学校受到影响的时间是2.4秒.
B
C
E
4.如图,MN表示某引水工程的一段设计路线,在M的北偏东60°的方向上有一点A,以A为中心周围600米范围内为居民区,取MN上另一点B,测得BA的方向为北偏东45°已知MB=400m
①如果不改变方向,那么输水路线是否会穿过居民区?
北
北
A
60°
45°
M
B
N
东
H
②若输水路线穿过居民区,求输水路线落在居民区内部分的长度(精确到1米)。
北
北
A
60°
45°
M
B
N
东
H
E
F
③为避免输水路线穿过居民区,在M点应怎样适当地调整输水线路的走向?
(偏转角度精确到1分)
北
北
A
60°
45°
M
B
N
东
G
(变式)如图,某货船以20海里/时的速度将一批重要物资由A处运往正西方向的B处,经16小时的航行到达,到达后必须立即卸货.此时,接到气象部门通知,一台风正以40海里/时的速度由A向北偏西60°方向移动.距台风中心200海里的圆形区域(包括边界)均会受到影响.
(1)问:B处是否受到台风的影响?请说明理由.
A
B
C
北
60°
320
160
●
∟
30°
(2)为避免受到台风的影响,该船应在多少小时内卸完货物?
A
C
60°
D
320
160
200
120
●
B
∟
30°
中考链接:1.如图,AC是普宁市环城路的一段,AE,BF,CD都是南北方向的街道,其与环城路AC的交叉路口分别是A,B,C.经测量花卉世界D位于点A的北偏东450方向、点B的北偏东300方向上,AB=2km,∠DAC=150.
(1)求B,D之间的距离;
(2)求C,D之间的距离.
