北师大版九年级下册2.3确定二次函数表达式课件(共23张ppt)
文档属性
| 名称 | 北师大版九年级下册2.3确定二次函数表达式课件(共23张ppt) |  | |
| 格式 | ppt | ||
| 文件大小 | 519.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 06:10:19 | ||
图片预览






文档简介
确定二次函数表达式(2)
学习目标:(1分钟)
1.会根据表格确定二次函数表达式
2.回顾不同条件下确定二次函数表达式
例1.某二次函数用表格表示如下:
x
…
-3
-2
-1
0
1
2
3
4
…
y
…
-29
-15
-5
1
3
1
-5
-15
…
(1)根据表格写出该函数图象:
对称轴:__________ 顶点坐标:__________
开口方向:__________ 最值:_____________
自学指导一(5分钟)
(2)求出这个函数的关系式.
直线x=1
(1,3)
向下
解:设y=a(x-1)2+3
设y=ax2+bx+c
(3)当x=5时, y=_______.
-29
当x=1, y最大=3
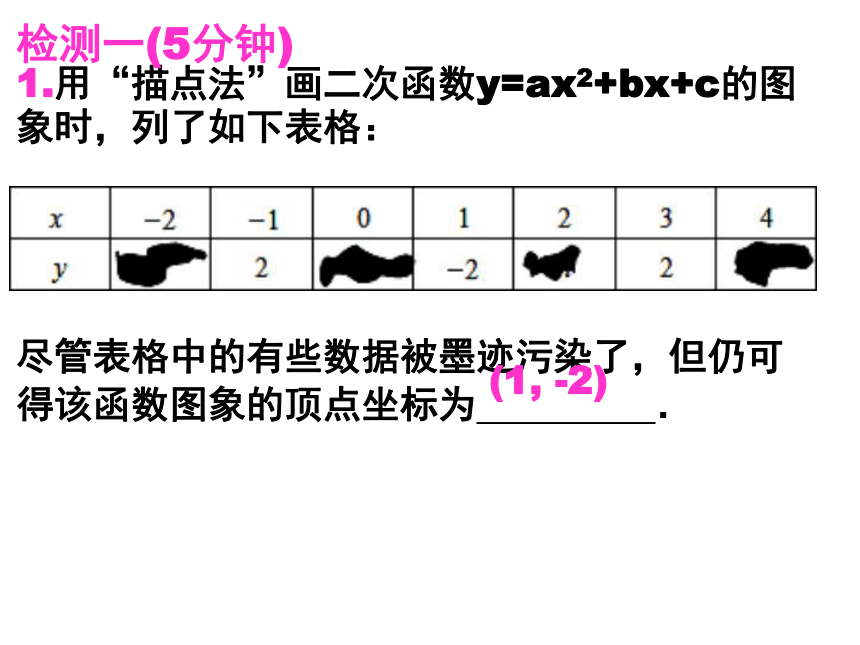
1.用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
?????????????????????????????????????????????????????????????
尽管表格中的有些数据被墨迹污染了,但仍可得该函数图象的顶点坐标为 .
检测一(5分钟)
(1, -2)
2. 画某个二次函数图象时,列了如下表格:
x
…
3
4
5
6
7
8
…
y
…
7.5
5
3.5
3
3.5
5
…
根据表格上的信息回答问题:该二次函数在x=9时, y=_________
7.5
3.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则当x=1时,y的值_____
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
4.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A (x1,y1)、B (x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时, y1 与y2的大小关系正确的是( )
X
...
0
1
2
3
4
...
y
...
4
1
0
1
4
...
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
5.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法正确的是_________
①抛物线的对称轴是直线x=1
②抛物线与y轴的交点为(0,6)
③抛物线与x轴的一个交点为(3,0)
④在对称轴左侧y随x的增大而增大
⑤ 函数y=-x2+bx+c的最大值为6
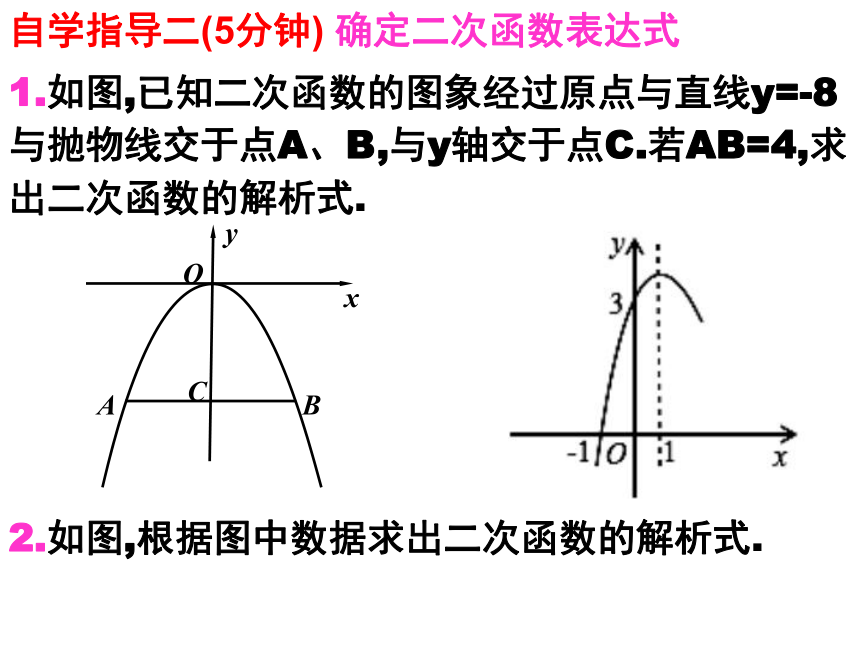
自学指导二(5分钟) 确定二次函数表达式
O
x
y
A
B
C
1.如图,已知二次函数的图象经过原点与直线y=-8与抛物线交于点A、B,与y轴交于点C.若AB=4,求出二次函数的解析式.
2.如图,根据图中数据求出二次函数的解析式.
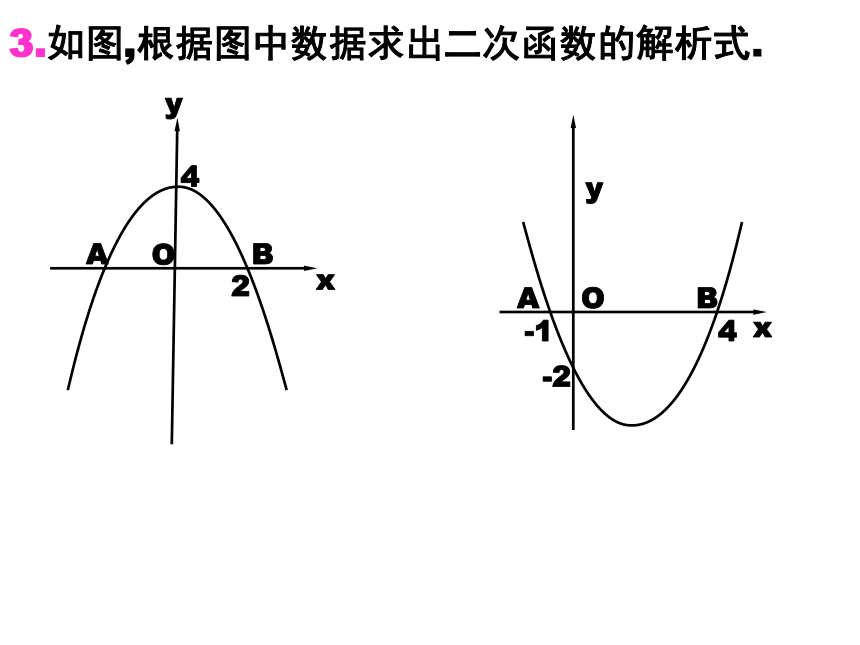
3.如图,根据图中数据求出二次函数的解析式.
O
x
y
A
B
2
4
O
x
y
A
B
4
-1
-2
4.如图,根据图中数据求出二次函数的解析式.
O
x
y
2
4
O
x
y
2
4
1
3.已知抛物线y=ax2+bx+c与x轴正,负半轴分别交于A、B两点,与y轴负半轴交于点C,若OA=4,OB=1,∠ACB=90°,求抛物线解析式.
解: ∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1, ∴点B(-1,0)
又 ∵ ∠ACB=90°
∴OC2=OA·OB=4
∴OC=2,点C(0,-2)
A
B
x
y
O
C
4.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,D是图象上的一点,M为抛物线的顶点.已知A(﹣1,0),C(0,5),D(1,8).
(1)求抛物线的解析式.
(2)求△MCB的面积.
1.如图,将抛物线y=? x2平移后经过原点O和点(6,0),平移后的抛物线的顶点为点B,对称轴与抛物线y=? x2相交于点C,则图中直线BC与两条抛物线围成的阴影部分的面积为_________
自学指导三:抛物线图像确定解析式(5分钟)
2.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是_______.
3.如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
5.如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
当堂训练
1.如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
O
D
C
B
A
X
Y
2.如图,一次函数y=kx+b的图像与x轴和y轴分别交于点A(-8,0),和点B(0,4),线段AB的垂直平分线交与x轴于点C,交AB于点D
(1)确定直线AB的解析式。
(2)求过A,B,C三点的抛物线解析式。
(3)抛物线对应的二次函数有最大值还有最小值?此时X等于多少?相应的最大值或最小值是多少?
3. 如图,矩形OABC的长OA= ,AB=1,将△AOC沿AC翻折得△APC。
(1)填空:∠PCB=___度,P点坐标为_____
(2)若P、A两点在抛物线y=- 4/3x2+bx+c 上,求抛物线的解析式,并判断点C是否在这抛物线上。
(3)在(2)中的抛物线CP段上(不含C、P点)是否存在一点M,使得四边形MCPA的面积最大?若存在,求这个最大值和M点坐标,若不存在,说明理由。
O
A
B
C
P
D
4.如图所示,已知二次函数图象的顶点坐标为C(1,0),直线y=mx+1与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上。
(1)求m的值及这个二次函数的关系式;
(2)P是线段AB上的一个动点(点P与A,B不重合),过P作X轴的垂线,与这个二次函数的图象交于E点,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由。
学习目标:(1分钟)
1.会根据表格确定二次函数表达式
2.回顾不同条件下确定二次函数表达式
例1.某二次函数用表格表示如下:
x
…
-3
-2
-1
0
1
2
3
4
…
y
…
-29
-15
-5
1
3
1
-5
-15
…
(1)根据表格写出该函数图象:
对称轴:__________ 顶点坐标:__________
开口方向:__________ 最值:_____________
自学指导一(5分钟)
(2)求出这个函数的关系式.
直线x=1
(1,3)
向下
解:设y=a(x-1)2+3
设y=ax2+bx+c
(3)当x=5时, y=_______.
-29
当x=1, y最大=3
1.用“描点法”画二次函数y=ax2+bx+c的图象时,列了如下表格:
?????????????????????????????????????????????????????????????
尽管表格中的有些数据被墨迹污染了,但仍可得该函数图象的顶点坐标为 .
检测一(5分钟)
(1, -2)
2. 画某个二次函数图象时,列了如下表格:
x
…
3
4
5
6
7
8
…
y
…
7.5
5
3.5
3
3.5
5
…
根据表格上的信息回答问题:该二次函数在x=9时, y=_________
7.5
3.若二次函数y=ax2+bx+c的x与y的部分对应值如下表:则当x=1时,y的值_____
x
-7
-6
-5
-4
-3
-2
y
-27
-13
-3
3
5
3
4.已知二次函数y=ax2+bx+c中,其函数y与自变量x之间的部分对应值如下表所示:
点A (x1,y1)、B (x2,y2)在函数的图象上,则当1<x1<2,3<x2<4时, y1 与y2的大小关系正确的是( )
X
...
0
1
2
3
4
...
y
...
4
1
0
1
4
...
A.y1>y2 B.y1<y2
C.y1≥y2 D.y1≤y2
5.抛物线y=-x2+bx+c上部分点的横坐标x,纵坐标y的对应值如下表:
x
…
-2
-1
0
1
2
…
y
…
0
4
6
6
4
…
从上表可知,下列说法正确的是_________
①抛物线的对称轴是直线x=1
②抛物线与y轴的交点为(0,6)
③抛物线与x轴的一个交点为(3,0)
④在对称轴左侧y随x的增大而增大
⑤ 函数y=-x2+bx+c的最大值为6
自学指导二(5分钟) 确定二次函数表达式
O
x
y
A
B
C
1.如图,已知二次函数的图象经过原点与直线y=-8与抛物线交于点A、B,与y轴交于点C.若AB=4,求出二次函数的解析式.
2.如图,根据图中数据求出二次函数的解析式.
3.如图,根据图中数据求出二次函数的解析式.
O
x
y
A
B
2
4
O
x
y
A
B
4
-1
-2
4.如图,根据图中数据求出二次函数的解析式.
O
x
y
2
4
O
x
y
2
4
1
3.已知抛物线y=ax2+bx+c与x轴正,负半轴分别交于A、B两点,与y轴负半轴交于点C,若OA=4,OB=1,∠ACB=90°,求抛物线解析式.
解: ∵点A在正半轴,点B在负半轴
OA=4,∴点A(4,0)
OB=1, ∴点B(-1,0)
又 ∵ ∠ACB=90°
∴OC2=OA·OB=4
∴OC=2,点C(0,-2)
A
B
x
y
O
C
4.如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A、B两点,与y轴交于C点,D是图象上的一点,M为抛物线的顶点.已知A(﹣1,0),C(0,5),D(1,8).
(1)求抛物线的解析式.
(2)求△MCB的面积.
1.如图,将抛物线y=? x2平移后经过原点O和点(6,0),平移后的抛物线的顶点为点B,对称轴与抛物线y=? x2相交于点C,则图中直线BC与两条抛物线围成的阴影部分的面积为_________
自学指导三:抛物线图像确定解析式(5分钟)
2.如图,边长为2的正方形ABCD的中心在直角坐标系的原点O,AD∥x轴,以O为顶点且过A、D两点的抛物线与以O为顶点且过B、C两点的抛物线将正方形分割成几部分.则图中阴影部分的面积是_______.
3.如图,已知:正方形ABCD边长为1,E、F、G、H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为s,AE为x,则s关于x的函数图象大致是( )
5.如图,Rt△ABC中,AC=BC=2,正方形CDEF的顶点D、F分别在AC、BC边上,C、D两点不重合,设CD的长度为x,△ABC与正方形CDEF重叠部分的面积为y,则下列图象中能表示y与x之间的函数关系的是( )
当堂训练
1.如图,二次函数y=ax2+bx-3的图象与x轴交于A(-1,0),B(3,0)两点,与y轴交于点C.该抛物线的顶点为M.
(1)求该抛物线的解析式;
(2)判断△BCM的形状,并说明理由;
(3)探究坐标轴上是否存在点P,使得以点P、A、C为顶点的三角形与△BCM相似?若存在,请直接写出点P的坐标;若不存在,请说明理由.
O
D
C
B
A
X
Y
2.如图,一次函数y=kx+b的图像与x轴和y轴分别交于点A(-8,0),和点B(0,4),线段AB的垂直平分线交与x轴于点C,交AB于点D
(1)确定直线AB的解析式。
(2)求过A,B,C三点的抛物线解析式。
(3)抛物线对应的二次函数有最大值还有最小值?此时X等于多少?相应的最大值或最小值是多少?
3. 如图,矩形OABC的长OA= ,AB=1,将△AOC沿AC翻折得△APC。
(1)填空:∠PCB=___度,P点坐标为_____
(2)若P、A两点在抛物线y=- 4/3x2+bx+c 上,求抛物线的解析式,并判断点C是否在这抛物线上。
(3)在(2)中的抛物线CP段上(不含C、P点)是否存在一点M,使得四边形MCPA的面积最大?若存在,求这个最大值和M点坐标,若不存在,说明理由。
O
A
B
C
P
D
4.如图所示,已知二次函数图象的顶点坐标为C(1,0),直线y=mx+1与该二次函数的图象交于A、B两点,其中A点的坐标为(3,4),B点在y轴上。
(1)求m的值及这个二次函数的关系式;
(2)P是线段AB上的一个动点(点P与A,B不重合),过P作X轴的垂线,与这个二次函数的图象交于E点,设线段PE的长为h,点P的横坐标为x,求h与x之间的函数关系式,并写出自变量x的取值范围;
(3)D为直线AB与这个二次函数图象对称轴的交点,在线段AB上是否存在一点P,使得四边形DCEP是平行四边形?若存在,请求出此时P点的坐标;若不存在,请说明理由。
