北师大版数学九年级下册 3.4 圆周角和圆心角的关系 课件(共25张ppt)
文档属性
| 名称 | 北师大版数学九年级下册 3.4 圆周角和圆心角的关系 课件(共25张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 670.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览


文档简介
圆周角和圆心角的关系
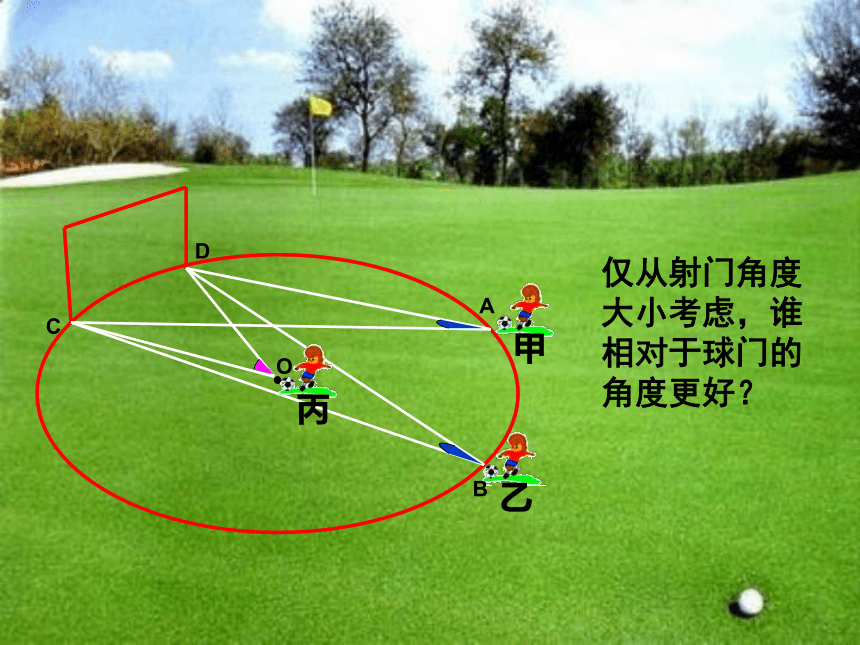
乙
甲
仅从射门角度大小考虑,谁相对于球门的角度更好?
A
B
C
D
O
丙
A
B
C
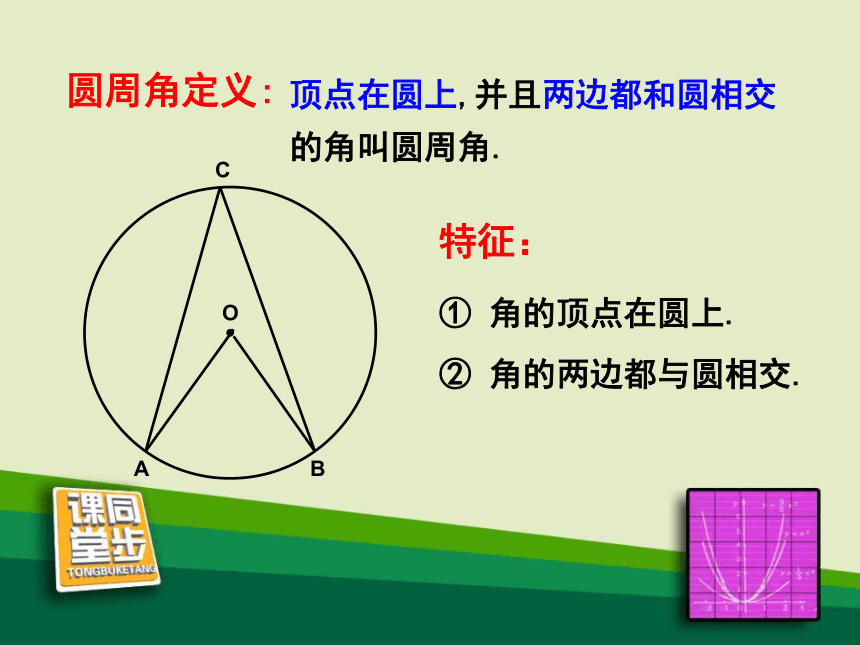
圆周角定义:
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
O
顶点在圆上,并且两边都和圆相交的角叫圆周角.
C
D
E
C
D
E
C
D
E
C
D
E
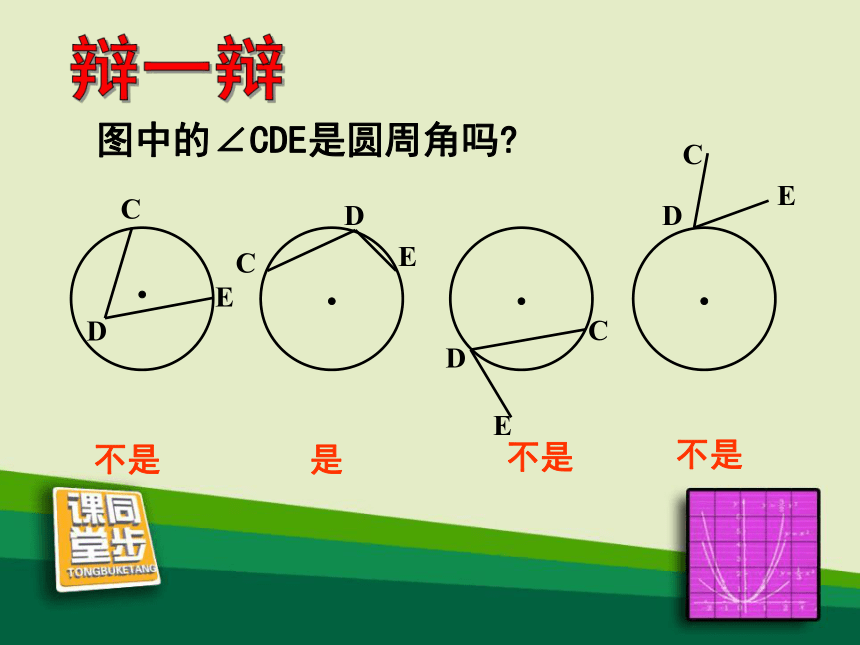
图中的∠CDE是圆周角吗?
不是
不是
是
不是
辩一辩
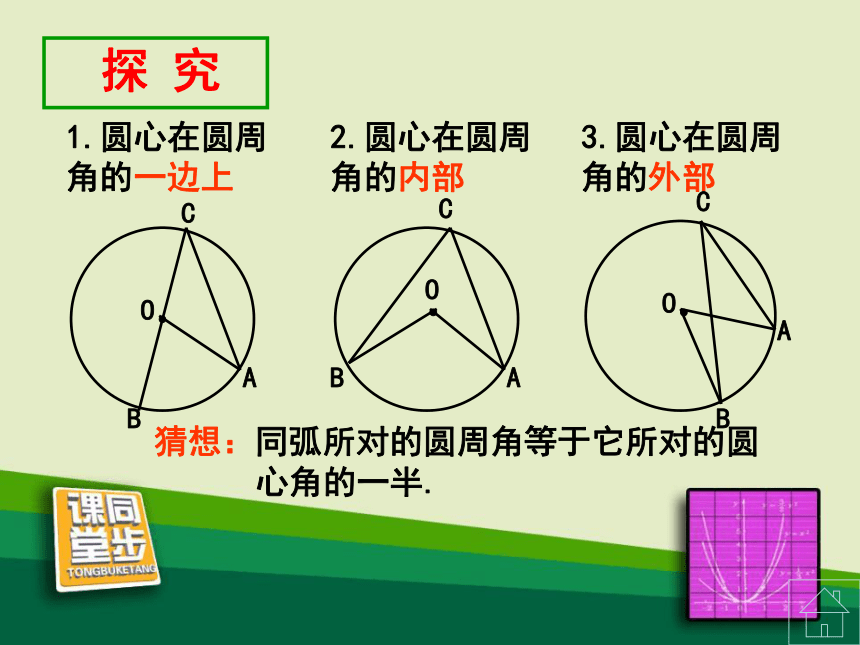
同弧所对圆周角与圆心角的关系
动手操作:在同一个圆中,画同弧所对圆周角 与圆心角 ,并且度量出你所画的圆周角和圆心角的大小.
注意:圆心与圆周角的位置
探 究
猜想:同弧所对的圆周角等于它所对的圆
心角的一半.
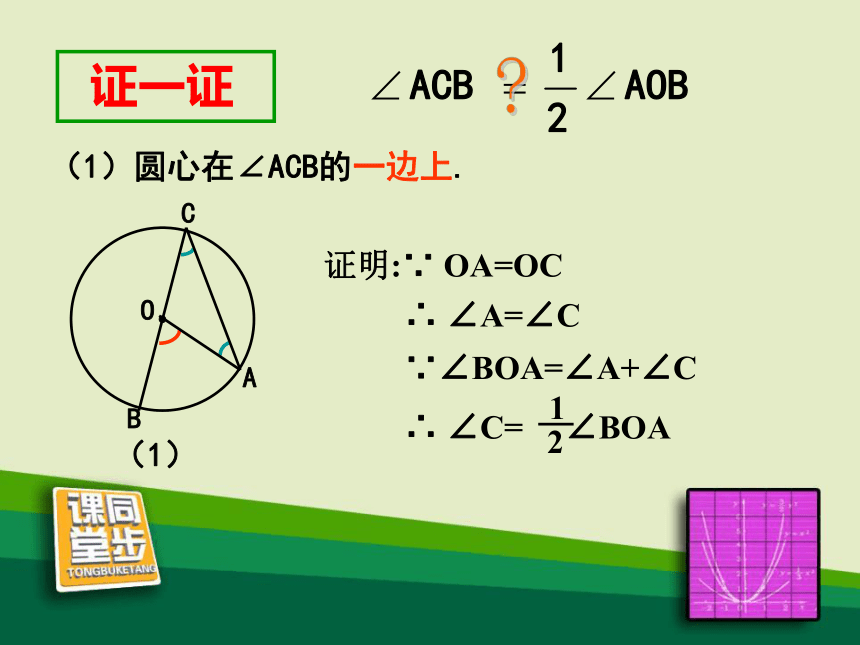
1.圆心在圆周角的一边上
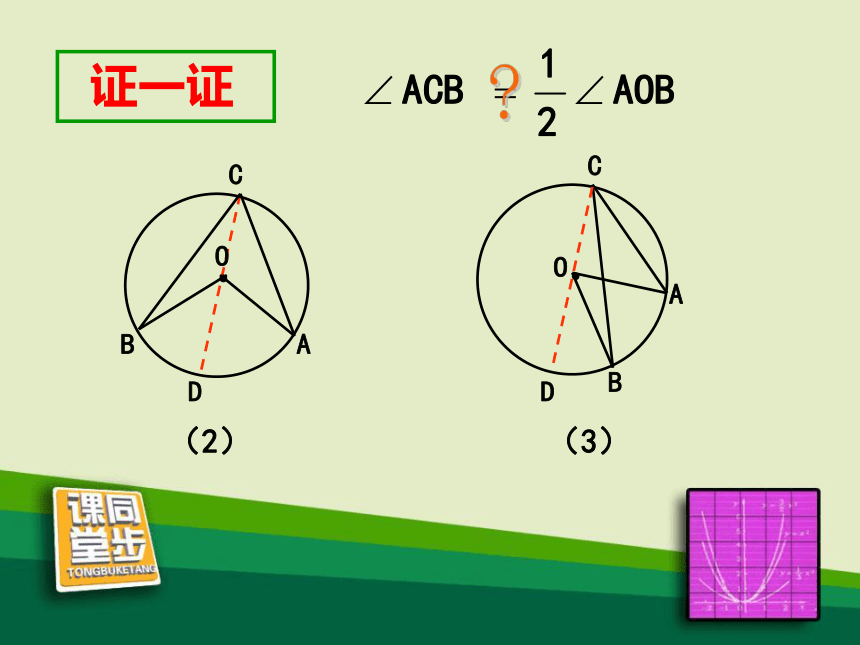
2.圆心在圆周角的内部
3.圆心在圆周角的外部
探 究
B
A
O
C
C
A
B
O
A
B
O
C
(1)
证明:∵ OA=OC
∴ ∠A=∠C
∵∠BOA=∠A+∠C
1
2
∴ ∠C= ∠BOA
?
(1)圆心在∠ACB的一边上.
证一证
B
A
O
C
D
(2)
(3)
?
证一证
C
A
B
O
A
B
O
C
D
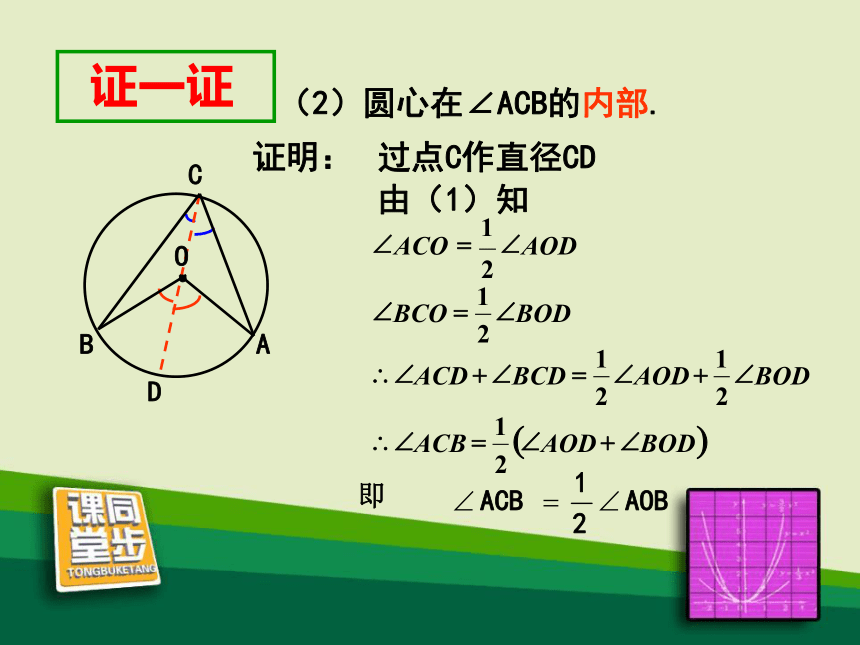
(2)圆心在∠ACB的内部.
由(1)知
即
证明:
过点C作直径CD
(
)
BOD
AOD
ACB
?
+
?
=
?
\
2
1
BOD
AOD
BCD
ACD
?
+
?
=
?
+
?
\
2
1
2
1
BOD
BCO
?
=
?
2
1
AOD
ACO
?
=
?
2
1
证一证
D
C
A
B
O
(3)圆心在∠ACB的外部.
证明:过点C作直径CD
由(1)知
即
(
)
BOD
AOD
ACB
?
-
?
=
?
\
2
1
BOD
AOD
BCO
ACO
?
-
?
=
?
-
?
\
2
1
2
1
BOD
BCO
?
=
?
2
1
AOD
ACO
?
=
?
2
1
证一证
(3)
A
B
O
C
D
D
D
在同圆或等圆中,同弧或等弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
归 纳
B
A
O
C
C
A
B
O
A
B
O
C
乙
甲
仅从射门角度大小考虑,谁相对于球门的角度更好?
A
B
C
D
O
丙
1.下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角
(B)60?的圆周角所对的弧的度数是30?
(C)一弧所对的圆周角等于它所对的圆心角
(D)120?的弧所对的圆周角是60?
基础训练
D
2.如右图,⊙O中,∠ACB = 130?, 则∠AOB=______.
B
A
O
C
1
100?
3.求圆中 的度数.
B
A
O
70°
C
A
O
120°
B
C
1
D
基础训练
A
B
C
D
O
4.如图, ,
则
=
25°
5.在半径为R的圆内,长为R的弦所对的圆周角为
30°
150°
或
O
A
B
再接再励
A
B
C
O
6.已知,⊙0 在 三边上截得的弦长相等,
,则 _______
130°
D
F
E
再接再励
O
A
B
C
即
又
1.如图,OA,OB,OC都是⊙0的半径,
与 的大小有什么关系?为什么?
证明:
能力提高
A
B
C
D
E
分析: 这五个圆周角所对的的弧之和正好是一个圆,一个圆所对的圆心角为
360°
2.如图,点A,B,C,D,E均在⊙0上,则
等于多少度?
为什么?
所以:
180°
=
能力提高
3.如图,在⊙O中,BC=2DE,∠BOC=84°,求∠A的度数.
O
C
B
D
E
能力提高
︵
︵
A
解:连接CD
∠BOC=84°
∴∠BDC=42°
又∵ BC=2DE
︵
︵
∴∠BDC=2∠ACD
∴∠ADC=21°
∵∠BDC= ∠BOC,
O
A
C
B
D
E
又∵∠BDC=∠ACD+∠A
∴∠A=∠BDC-∠ADC =42°-21°=21°
1.本节课学习了哪些新知识?
2.运用了哪些已学的知识?
3.在学习过程中运用了什么样的方法解决问题?
课堂小结
化归
化归
圆周角定理
分类讨论
数学思想
D
C
A
B
O
B
A
O
C
D
A
B
O
C
分层作业:
必做题:教科书112页第2,3题
选做题:
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
⌒ ⌒
BD=DE
A
B
C
D
E
求证:
乙
甲
仅从射门角度大小考虑,谁相对于球门的角度更好?
A
B
C
D
O
丙
A
B
C
圆周角定义:
特征:
① 角的顶点在圆上.
② 角的两边都与圆相交.
O
顶点在圆上,并且两边都和圆相交的角叫圆周角.
C
D
E
C
D
E
C
D
E
C
D
E
图中的∠CDE是圆周角吗?
不是
不是
是
不是
辩一辩
同弧所对圆周角与圆心角的关系
动手操作:在同一个圆中,画同弧所对圆周角 与圆心角 ,并且度量出你所画的圆周角和圆心角的大小.
注意:圆心与圆周角的位置
探 究
猜想:同弧所对的圆周角等于它所对的圆
心角的一半.
1.圆心在圆周角的一边上
2.圆心在圆周角的内部
3.圆心在圆周角的外部
探 究
B
A
O
C
C
A
B
O
A
B
O
C
(1)
证明:∵ OA=OC
∴ ∠A=∠C
∵∠BOA=∠A+∠C
1
2
∴ ∠C= ∠BOA
?
(1)圆心在∠ACB的一边上.
证一证
B
A
O
C
D
(2)
(3)
?
证一证
C
A
B
O
A
B
O
C
D
(2)圆心在∠ACB的内部.
由(1)知
即
证明:
过点C作直径CD
(
)
BOD
AOD
ACB
?
+
?
=
?
\
2
1
BOD
AOD
BCD
ACD
?
+
?
=
?
+
?
\
2
1
2
1
BOD
BCO
?
=
?
2
1
AOD
ACO
?
=
?
2
1
证一证
D
C
A
B
O
(3)圆心在∠ACB的外部.
证明:过点C作直径CD
由(1)知
即
(
)
BOD
AOD
ACB
?
-
?
=
?
\
2
1
BOD
AOD
BCO
ACO
?
-
?
=
?
-
?
\
2
1
2
1
BOD
BCO
?
=
?
2
1
AOD
ACO
?
=
?
2
1
证一证
(3)
A
B
O
C
D
D
D
在同圆或等圆中,同弧或等弧所对的圆周角等于它所对的圆心角的一半.
圆周角定理:
归 纳
B
A
O
C
C
A
B
O
A
B
O
C
乙
甲
仅从射门角度大小考虑,谁相对于球门的角度更好?
A
B
C
D
O
丙
1.下列命题中是真命题的是( )
(A)顶点在圆周上的角叫做圆周角
(B)60?的圆周角所对的弧的度数是30?
(C)一弧所对的圆周角等于它所对的圆心角
(D)120?的弧所对的圆周角是60?
基础训练
D
2.如右图,⊙O中,∠ACB = 130?, 则∠AOB=______.
B
A
O
C
1
100?
3.求圆中 的度数.
B
A
O
70°
C
A
O
120°
B
C
1
D
基础训练
A
B
C
D
O
4.如图, ,
则
=
25°
5.在半径为R的圆内,长为R的弦所对的圆周角为
30°
150°
或
O
A
B
再接再励
A
B
C
O
6.已知,⊙0 在 三边上截得的弦长相等,
,则 _______
130°
D
F
E
再接再励
O
A
B
C
即
又
1.如图,OA,OB,OC都是⊙0的半径,
与 的大小有什么关系?为什么?
证明:
能力提高
A
B
C
D
E
分析: 这五个圆周角所对的的弧之和正好是一个圆,一个圆所对的圆心角为
360°
2.如图,点A,B,C,D,E均在⊙0上,则
等于多少度?
为什么?
所以:
180°
=
能力提高
3.如图,在⊙O中,BC=2DE,∠BOC=84°,求∠A的度数.
O
C
B
D
E
能力提高
︵
︵
A
解:连接CD
∠BOC=84°
∴∠BDC=42°
又∵ BC=2DE
︵
︵
∴∠BDC=2∠ACD
∴∠ADC=21°
∵∠BDC= ∠BOC,
O
A
C
B
D
E
又∵∠BDC=∠ACD+∠A
∴∠A=∠BDC-∠ADC =42°-21°=21°
1.本节课学习了哪些新知识?
2.运用了哪些已学的知识?
3.在学习过程中运用了什么样的方法解决问题?
课堂小结
化归
化归
圆周角定理
分类讨论
数学思想
D
C
A
B
O
B
A
O
C
D
A
B
O
C
分层作业:
必做题:教科书112页第2,3题
选做题:
已知:如图,在△ABC中,AB=AC,
以AB为直径的圆交BC于D,交AC于E,
⌒ ⌒
BD=DE
A
B
C
D
E
求证:
