沪教版(上海)数学八年级第二学期-23.3 事件的概率 课件(共26张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-23.3 事件的概率 课件(共26张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 06:17:31 | ||
图片预览








文档简介
投篮入筐是随机事件
经过专业人士测算, 他们罚篮命中的概率
72.3%
62.3%
82.3%
88.7%
我会选择姚明
23.3 事件的概率
第一课时
概念
概率:
用来表示某事件发生的可能性的大小的数叫做这个事件的概率
摸牌实验
实验要求:
1.每大组6位同学进行摸牌实验,先以2位同学为1组进行摸牌,然后大组组长最终进行统计。小组摸牌时间:3分钟。组长统计时间:1分钟
2.一共有3张牌,分别为红色牌1、2、3。每次只能由一名同学任意摸牌一次,每次把摸出的牌放回再次洗匀,反复进行试验。
3.摸牌实验由两位同学完成,一人负责摸牌与记录,另一位同学负责洗牌(记录牌时可以用“正”字)。
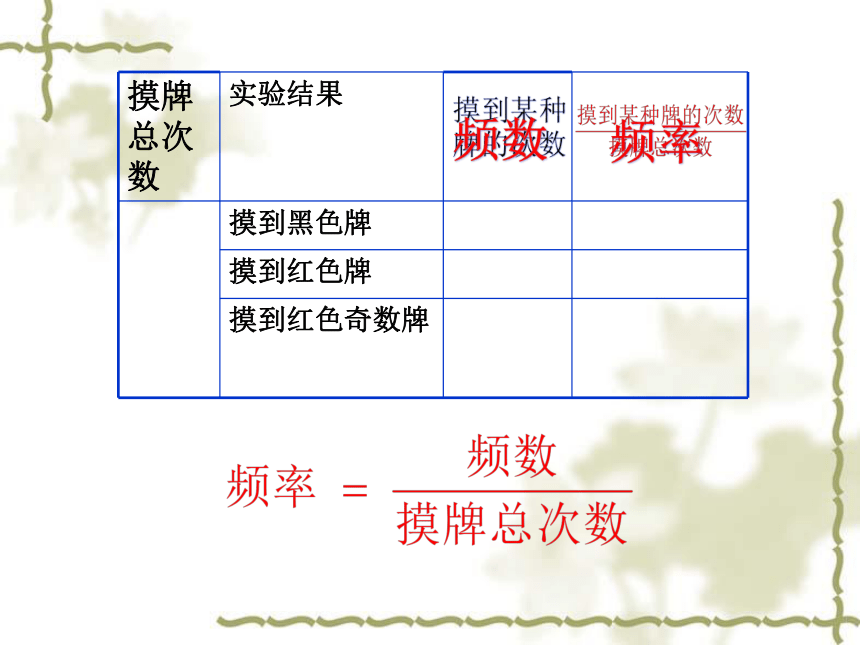
摸牌总次数
实验结果
摸到黑色牌
摸到红色牌
摸到红色奇数牌
摸到某种牌的次数
频数
频率
1.在摸牌活动中摸到黑牌是________,而摸到黑牌的频率为______
2. 在摸牌活动中摸到红牌是________,而摸到红牌的频率是_____.
3.在摸牌活动中摸到红色奇数牌是________,
而摸到红色的奇数牌的频率___________,在操
作次数相对较大时,频率接近于_________
不可能事件
0
随机事件
1
必然事件
都不相同
?
随机事件的概率
必然事件的概率
不可能事件的概率
一般用大写字母A,B,C…表示事件。如事件A的概率,记作P(A)
事件概率的取值情况
0
1
用V表示不可能事件,U表示必然事件,
那么P(V)=0,P(U)=1
随机事件A,则 0< P(A)<1
让我们来再做一个试验:
试验:把一枚硬币抛多次,观察其出现的结果,并记录各结果出现的频数,然后计算各频率。
将实验结果填入下表:
抛掷次数
实验结果
频数
频率
表一:
投掷一枚硬币,出现正面可能性有多大?
你发现了什么呢?
吴老师的发现:
(1)在实验中只出现了2种实验结果。 (2)每一次试验中的一个实验结果的频率都不相同,但都接近一个数,0.5 (3)随着试验次数的增加,试验的频率往往更接近0.5
(4)试验中,投掷硬币的正面与反面的频率是差不多大的,可以猜想它们得可能性是一样的。
难怪足球比赛中要用扔硬币来决定开球
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次数(m)
1061
2048
6019
12012
14984
频率(m/n)
0.518
0.506
0.501
0.5005
0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
在上述抛掷硬币的试验中,
正面向上发生的频率的
稳定值为多少?
0.5
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率m/n
1902
954
470
194
92
45
优等品数
2000
1000
500
200
100
50
抽取球数
(附表2:某批乒乓球产品质量检查结果表)
当抽查的球数很多时,优等品的频率接近于常数0.95
500
抽取球数n
1000
2000
频率m/n
50
100
200
0.95
1
观察分析频率的变化规律:
每批粒数n
2
5
10
70
130
310
700
1500
2000
3000
发芽的粒数 m
2
4
9
60
116
282
639
1339
1806
2715
发芽的频率m/n
1
0.8
0.9
0.857
0.892
0.910
0.913
0.893
0.903
0.905
每批粒数n
频率m/n
0.9
1
2
5
10
130
700
2000
70
310
1500
3000
(附表3:某种油菜籽在相同条件下的发芽试验结果表)
当试验的油菜籽的粒数很多时,油菜籽发芽的频率接近于常数0.9
随机事件A 在每
次试验中是否发生是
不能事先确定的,但
是在进行大数量重复
试验后,随着试验次
数的增加,事件A发
生的频率总是接近于
某个常数.
结论:
通过观察以上试验结果及频率图,它们的规律有什么共性呢?
概率的定义:
说明:
(1)概率从数量上反映了一个事件发生的可能性的大小;
(2)概率是频率的稳定值,而频率是概率的近似值;
(3) 事件A的概率范围.
很明显:必然事件的概率1,不可能事件的概率是0.
0≤P(A)≤1
在相同的条件下,大量重复进行同一试验时,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性,这时我们就把这个常数叫做随机事件A的概率,记作P(A).
课外研究
雅各布·伯努利
(Jacob Bernoulli)
(1654~1705)
瑞士数学家
1713年出版《猜度术》,给出「伯努利数」、「伯努利大数定律」
我们现在所做的多次试验也称之为伯努利试验
下列说法:
(1)频率反映事件发生的频繁程度,概率反映事件发生的可能性
(2)做n次随机试验,事件A发生的频率就是事件A的概率
(3)频率是不能脱离n次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值
(4)频率是概率的近似值.
其中正确的是_________
(1)(3)(4)
动脑想一想
游戏1
你能猜出玩家手中的三张牌吗?
小试牛刀
全班同学一起做摸球试验,布袋里的球除了颜色外其它都一样,每次从布袋里摸出一个球,记下颜色后放回摇匀,一共摸了200次,其中131次摸出红球,69次摸出白球,如果布袋里有3个球,请你估计布袋里红球和白球的个数
小试牛刀
写出下列事件的概率(很可能发生的事情,填接近于1.若是小概率事件,填接近于0)
1、用A表示“上海天天是晴天”,则P(A) ( )
2、用B表示“新买的圆珠笔写得出字”,则P(B) ( )
3、用C表示“坐火车出行,遭遇出轨”,则P(C) ( )
4、用D表示“当m是正整数时,2m是偶数”,则P(D) ( )
课堂小结、随机事件的频率与概率的关系:
概 率
频 率
随机事件
确定的
试验
随机的
随机的
估计
大量的重复
稳定于某常数
布置作业
练习册 习题 23.3 (1)
再见!
经过专业人士测算, 他们罚篮命中的概率
72.3%
62.3%
82.3%
88.7%
我会选择姚明
23.3 事件的概率
第一课时
概念
概率:
用来表示某事件发生的可能性的大小的数叫做这个事件的概率
摸牌实验
实验要求:
1.每大组6位同学进行摸牌实验,先以2位同学为1组进行摸牌,然后大组组长最终进行统计。小组摸牌时间:3分钟。组长统计时间:1分钟
2.一共有3张牌,分别为红色牌1、2、3。每次只能由一名同学任意摸牌一次,每次把摸出的牌放回再次洗匀,反复进行试验。
3.摸牌实验由两位同学完成,一人负责摸牌与记录,另一位同学负责洗牌(记录牌时可以用“正”字)。
摸牌总次数
实验结果
摸到黑色牌
摸到红色牌
摸到红色奇数牌
摸到某种牌的次数
频数
频率
1.在摸牌活动中摸到黑牌是________,而摸到黑牌的频率为______
2. 在摸牌活动中摸到红牌是________,而摸到红牌的频率是_____.
3.在摸牌活动中摸到红色奇数牌是________,
而摸到红色的奇数牌的频率___________,在操
作次数相对较大时,频率接近于_________
不可能事件
0
随机事件
1
必然事件
都不相同
?
随机事件的概率
必然事件的概率
不可能事件的概率
一般用大写字母A,B,C…表示事件。如事件A的概率,记作P(A)
事件概率的取值情况
0
1
用V表示不可能事件,U表示必然事件,
那么P(V)=0,P(U)=1
随机事件A,则 0< P(A)<1
让我们来再做一个试验:
试验:把一枚硬币抛多次,观察其出现的结果,并记录各结果出现的频数,然后计算各频率。
将实验结果填入下表:
抛掷次数
实验结果
频数
频率
表一:
投掷一枚硬币,出现正面可能性有多大?
你发现了什么呢?
吴老师的发现:
(1)在实验中只出现了2种实验结果。 (2)每一次试验中的一个实验结果的频率都不相同,但都接近一个数,0.5 (3)随着试验次数的增加,试验的频率往往更接近0.5
(4)试验中,投掷硬币的正面与反面的频率是差不多大的,可以猜想它们得可能性是一样的。
难怪足球比赛中要用扔硬币来决定开球
抛掷次数(n)
2048
4040
12000
24000
30000
正面朝上次数(m)
1061
2048
6019
12012
14984
频率(m/n)
0.518
0.506
0.501
0.5005
0.4996
历史上曾有人作过抛掷硬币的大量重复实验,结果如下表所示
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
德 . 摩根
蒲 丰
皮尔逊
皮尔逊
维 尼
在上述抛掷硬币的试验中,
正面向上发生的频率的
稳定值为多少?
0.5
0.951
0.954
0.94
0.97
0.92
0.9
优等品频率m/n
1902
954
470
194
92
45
优等品数
2000
1000
500
200
100
50
抽取球数
(附表2:某批乒乓球产品质量检查结果表)
当抽查的球数很多时,优等品的频率接近于常数0.95
500
抽取球数n
1000
2000
频率m/n
50
100
200
0.95
1
观察分析频率的变化规律:
每批粒数n
2
5
10
70
130
310
700
1500
2000
3000
发芽的粒数 m
2
4
9
60
116
282
639
1339
1806
2715
发芽的频率m/n
1
0.8
0.9
0.857
0.892
0.910
0.913
0.893
0.903
0.905
每批粒数n
频率m/n
0.9
1
2
5
10
130
700
2000
70
310
1500
3000
(附表3:某种油菜籽在相同条件下的发芽试验结果表)
当试验的油菜籽的粒数很多时,油菜籽发芽的频率接近于常数0.9
随机事件A 在每
次试验中是否发生是
不能事先确定的,但
是在进行大数量重复
试验后,随着试验次
数的增加,事件A发
生的频率总是接近于
某个常数.
结论:
通过观察以上试验结果及频率图,它们的规律有什么共性呢?
概率的定义:
说明:
(1)概率从数量上反映了一个事件发生的可能性的大小;
(2)概率是频率的稳定值,而频率是概率的近似值;
(3) 事件A的概率范围.
很明显:必然事件的概率1,不可能事件的概率是0.
0≤P(A)≤1
在相同的条件下,大量重复进行同一试验时,随机事件A发生的频率会在某个常数附近摆动,即随机事件A发生的频率具有稳定性,这时我们就把这个常数叫做随机事件A的概率,记作P(A).
课外研究
雅各布·伯努利
(Jacob Bernoulli)
(1654~1705)
瑞士数学家
1713年出版《猜度术》,给出「伯努利数」、「伯努利大数定律」
我们现在所做的多次试验也称之为伯努利试验
下列说法:
(1)频率反映事件发生的频繁程度,概率反映事件发生的可能性
(2)做n次随机试验,事件A发生的频率就是事件A的概率
(3)频率是不能脱离n次试验的试验值,而概率是具有确定性的不依赖于试验次数的理论值
(4)频率是概率的近似值.
其中正确的是_________
(1)(3)(4)
动脑想一想
游戏1
你能猜出玩家手中的三张牌吗?
小试牛刀
全班同学一起做摸球试验,布袋里的球除了颜色外其它都一样,每次从布袋里摸出一个球,记下颜色后放回摇匀,一共摸了200次,其中131次摸出红球,69次摸出白球,如果布袋里有3个球,请你估计布袋里红球和白球的个数
小试牛刀
写出下列事件的概率(很可能发生的事情,填接近于1.若是小概率事件,填接近于0)
1、用A表示“上海天天是晴天”,则P(A) ( )
2、用B表示“新买的圆珠笔写得出字”,则P(B) ( )
3、用C表示“坐火车出行,遭遇出轨”,则P(C) ( )
4、用D表示“当m是正整数时,2m是偶数”,则P(D) ( )
课堂小结、随机事件的频率与概率的关系:
概 率
频 率
随机事件
确定的
试验
随机的
随机的
估计
大量的重复
稳定于某常数
布置作业
练习册 习题 23.3 (1)
再见!
