沪教版(上海)数学九年级第二学期-27.1 圆的确定 课件(共0张ppt)
文档属性
| 名称 | 沪教版(上海)数学九年级第二学期-27.1 圆的确定 课件(共0张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览





文档简介
27.1圆的确定
你有什么方法使得我能“破镜重圆”呢?
返回
圆的定义:圆是平面上到一个定点的距离等于定长的
所有点所成的图形.
这个定点叫圆心.
联结圆心和圆上任意一点的线段是圆的半
径,这个定长是圆的半径长.
圆的表示方法:以点O为圆心的圆称为圆O,记作⊙O
●
●
●
●
●
●
点与圆的位
置关系
点在圆外
点在圆上
点在圆内
返回
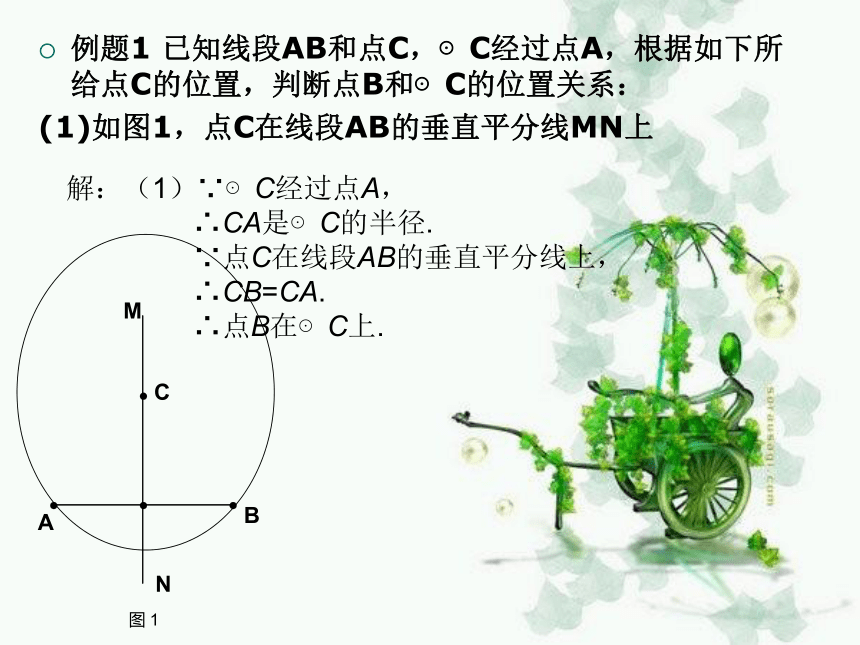
例题1 已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B和⊙C的位置关系:
(1)如图1,点C在线段AB的垂直平分线MN上
解:(1)∵⊙C经过点A,
∴CA是⊙C的半径.
∵点C在线段AB的垂直平分线上,
∴CB=CA.
∴点B在⊙C上.
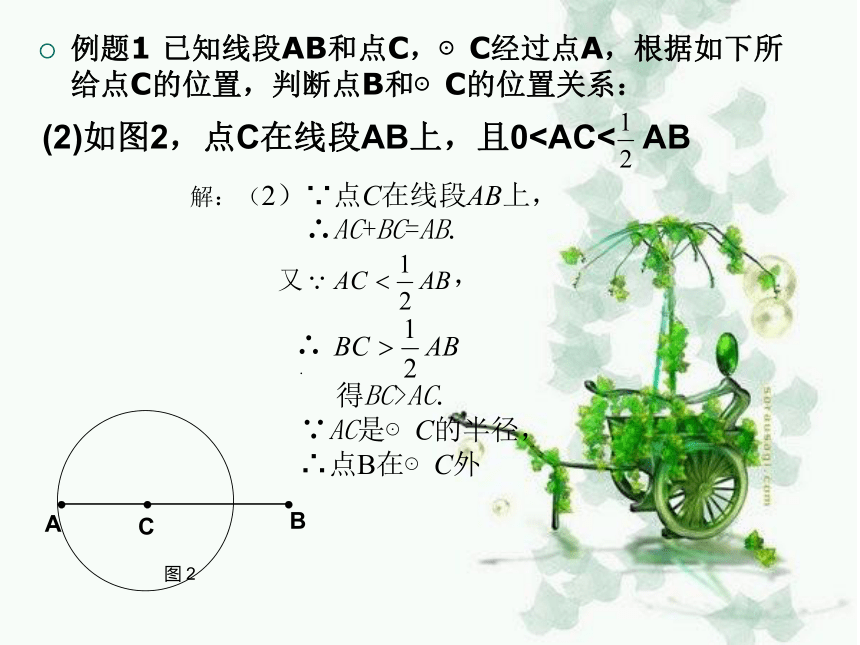
例题1 已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B和⊙C的位置关系:
(2)如图2,点C在线段AB上,且0解:(2)∵点C在线段AB上,
∴AC+BC=AB.
,
∴
.
得BC>AC.
∵AC是⊙C的半径,
∴点B在⊙C外
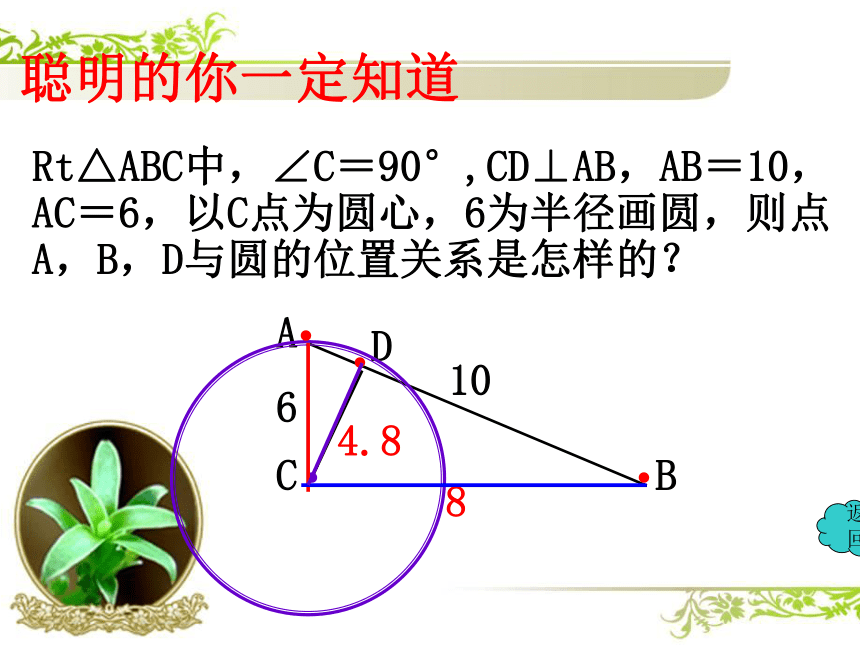
聪明的你一定知道
Rt△ABC中,∠C=90°,CD⊥AB,AB=10,AC=6,以C点为圆心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?
C
A
B
D
6
10
8
4.8
.
.
.
.
返回
A
.
过一点可以
画无数个圆
.
过一点作圆
123
.
.
A
B
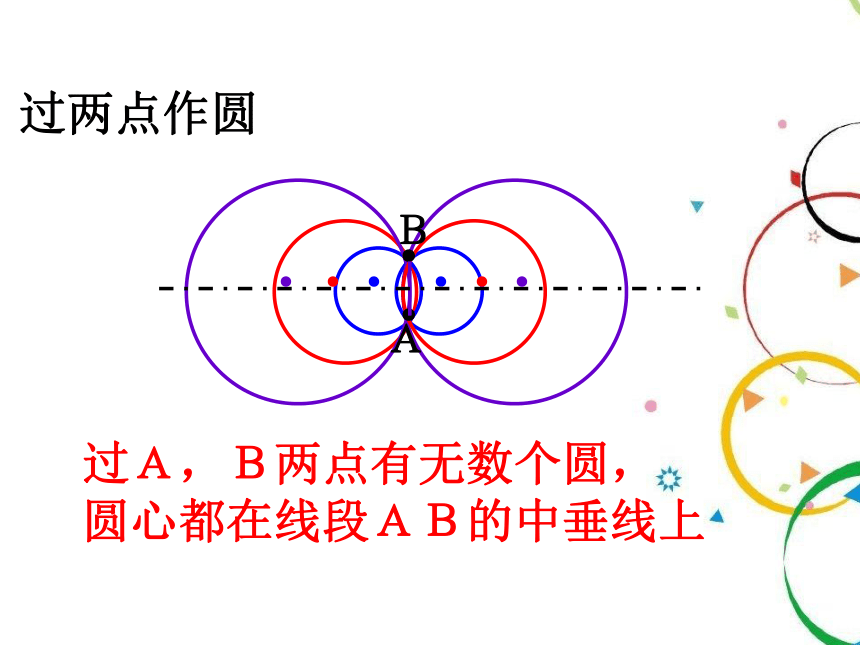
过A,B两点有无数个圆,
圆心都在线段AB的中垂线上
.
.
.
.
.
.
过两点作圆
.
.
.
A
B
C
.
O
定理 不在同一条直线上的三个点确定 一个圆
经过不在同一直线上三点作圆
如果A,B,C三点
在一条直线上,
经过这三点
你能画圆吗?
A
C
B
.
.
.
.
.
.
A
B
C
.
O
经过三角形三个顶点可以画一个圆,并且只能画一个.
经过三角形三个顶点的圆叫做三角形的外接圆.
三角形外接圆的圆心叫做这个三角形的外心;
外心就是三角形三条边的垂直平分线的交点.
这个三角形叫做这个圆的内接三角形.
△ABC
⊙O
.
O
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆
这个多边形叫做这个圆的内接多边形.
品尝仔细带来的喜悦!
判断正误
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且
只有一个内接三角形.
4.三角形的外心到三角形各个顶点的
距离都相等.
(×)
(√)
(×)
(√)
你有什么方法使得我能“破镜重圆”呢?
返回
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
已知锐角三角形ABC(图3),直角三角形A1B1C1(图4),钝角三角形A2B2C2(图5)
分别作出这三个三角形的外接圆
比较这三个三角形外心的位置,你能有什么发现?
1.点与圆的位置关系
2.过点作圆
(1)过一点作圆
(2)过两点作圆
(3)过三点作圆
3.三角形的外接圆
今天我们学到了……
返回
三、思考题:
经过四个点是不是一定能作圆?
分类
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆。
D
4、
A
B
C
A
B
C
D
3、
B
A
C
D
你强,我更强!
1. 如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?
2.一个点P到⊙O上所有点的距离中,
最大距离是8,最小距离是3,那么
⊙O的半径长是多少?
谢谢大家!
你有什么方法使得我能“破镜重圆”呢?
返回
圆的定义:圆是平面上到一个定点的距离等于定长的
所有点所成的图形.
这个定点叫圆心.
联结圆心和圆上任意一点的线段是圆的半
径,这个定长是圆的半径长.
圆的表示方法:以点O为圆心的圆称为圆O,记作⊙O
●
●
●
●
●
●
点与圆的位
置关系
点在圆外
点在圆上
点在圆内
返回
例题1 已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B和⊙C的位置关系:
(1)如图1,点C在线段AB的垂直平分线MN上
解:(1)∵⊙C经过点A,
∴CA是⊙C的半径.
∵点C在线段AB的垂直平分线上,
∴CB=CA.
∴点B在⊙C上.
例题1 已知线段AB和点C,⊙C经过点A,根据如下所给点C的位置,判断点B和⊙C的位置关系:
(2)如图2,点C在线段AB上,且0
∴AC+BC=AB.
,
∴
.
得BC>AC.
∵AC是⊙C的半径,
∴点B在⊙C外
聪明的你一定知道
Rt△ABC中,∠C=90°,CD⊥AB,AB=10,AC=6,以C点为圆心,6为半径画圆,则点A,B,D与圆的位置关系是怎样的?
C
A
B
D
6
10
8
4.8
.
.
.
.
返回
A
.
过一点可以
画无数个圆
.
过一点作圆
123
.
.
A
B
过A,B两点有无数个圆,
圆心都在线段AB的中垂线上
.
.
.
.
.
.
过两点作圆
.
.
.
A
B
C
.
O
定理 不在同一条直线上的三个点确定 一个圆
经过不在同一直线上三点作圆
如果A,B,C三点
在一条直线上,
经过这三点
你能画圆吗?
A
C
B
.
.
.
.
.
.
A
B
C
.
O
经过三角形三个顶点可以画一个圆,并且只能画一个.
经过三角形三个顶点的圆叫做三角形的外接圆.
三角形外接圆的圆心叫做这个三角形的外心;
外心就是三角形三条边的垂直平分线的交点.
这个三角形叫做这个圆的内接三角形.
△ABC
⊙O
.
O
如果一个圆经过一个多边形的各顶点,
那么这个圆叫做这个多边形的外接圆
这个多边形叫做这个圆的内接多边形.
品尝仔细带来的喜悦!
判断正误
1.经过三个点一定可以作圆.
2.任意一个三角形一定有一个外接圆.
3.任意一个圆一定有一内接三角形,并且
只有一个内接三角形.
4.三角形的外心到三角形各个顶点的
距离都相等.
(×)
(√)
(×)
(√)
你有什么方法使得我能“破镜重圆”呢?
返回
如何解决“破镜重圆”的问题:
解决问题的关键是什么?
(找圆心)
A
B
C
O
已知锐角三角形ABC(图3),直角三角形A1B1C1(图4),钝角三角形A2B2C2(图5)
分别作出这三个三角形的外接圆
比较这三个三角形外心的位置,你能有什么发现?
1.点与圆的位置关系
2.过点作圆
(1)过一点作圆
(2)过两点作圆
(3)过三点作圆
3.三角形的外接圆
今天我们学到了……
返回
三、思考题:
经过四个点是不是一定能作圆?
分类
1、
A
B
C
D
2、
A
B
C
D
所以经过四点不一定能作圆。
D
4、
A
B
C
A
B
C
D
3、
B
A
C
D
你强,我更强!
1. 如果直角三角形的两条直角边分别是6,8,你能求出这个直角三角形的外接圆的半径吗?是多少?
2.一个点P到⊙O上所有点的距离中,
最大距离是8,最小距离是3,那么
⊙O的半径长是多少?
谢谢大家!
