沪教版(上海)数学七年级下册14.6(1) 等腰三角形的判定 课件(共15张ppt)
文档属性
| 名称 | 沪教版(上海)数学七年级下册14.6(1) 等腰三角形的判定 课件(共15张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 450.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览


文档简介
14.6(1)
等腰三角形的判定
A
B
O
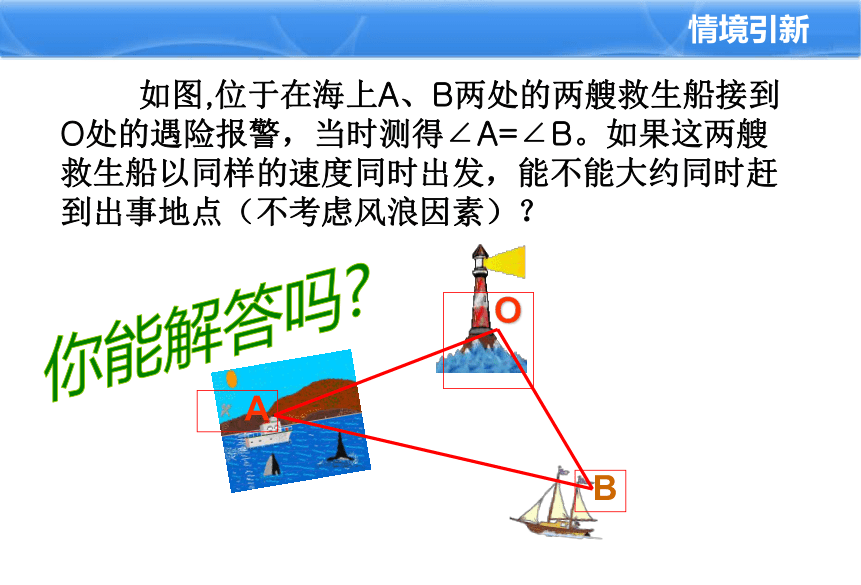
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
你能解答吗?
情境引新
新课探索
Part 1
Part 2
论证猜想
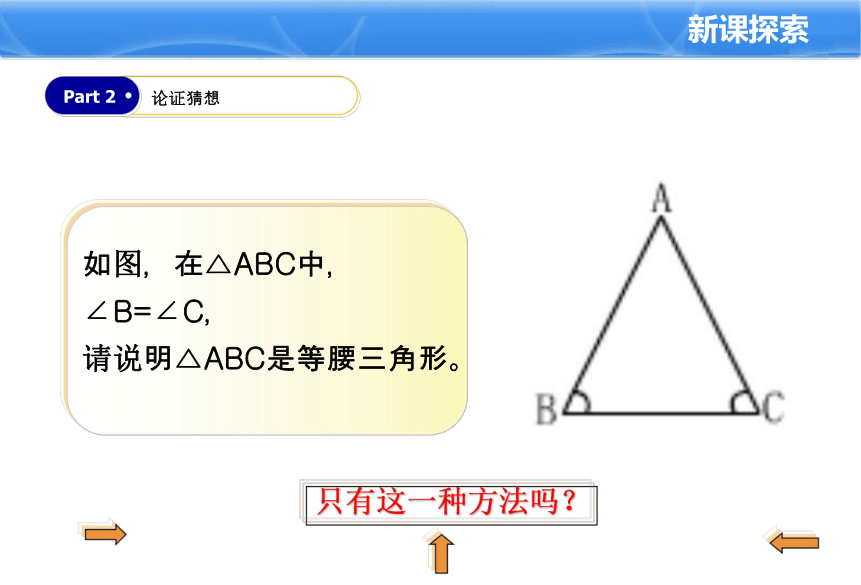
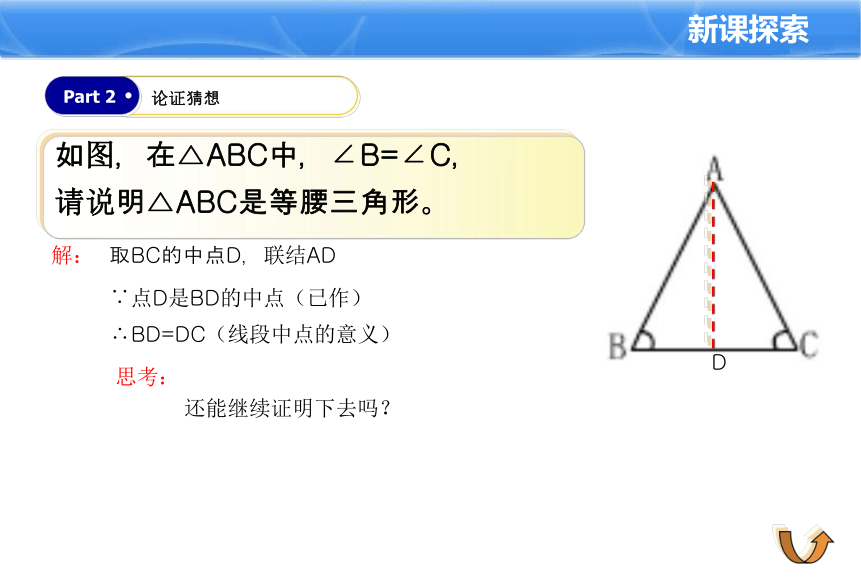
如图,在△ABC中,
∠B=∠C,
请说明△ABC是等腰三角形。
只有这一种方法吗?
新课探索
Part 1
Part 2
论证猜想
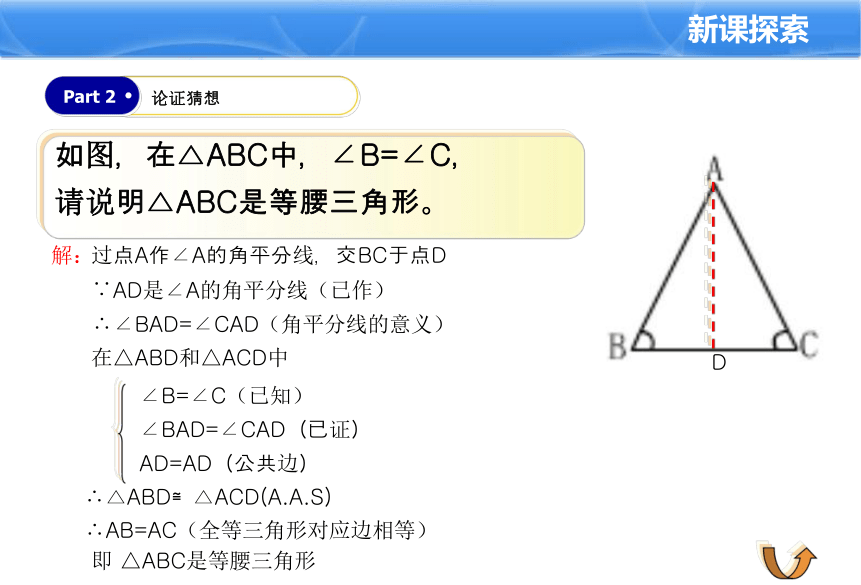
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
过点A作∠A的角平分线,交BC于点D
D
∵AD是∠A的角平分线(已作)
∴∠BAD=∠CAD(角平分线的意义)
在△ABD和△ACD中
∠B=∠C(已知)
∠BAD=∠CAD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(A.A.S)
∴AB=AC(全等三角形对应边相等)
即 △ABC是等腰三角形
新课探索
Part 1
Part 2
论证猜想
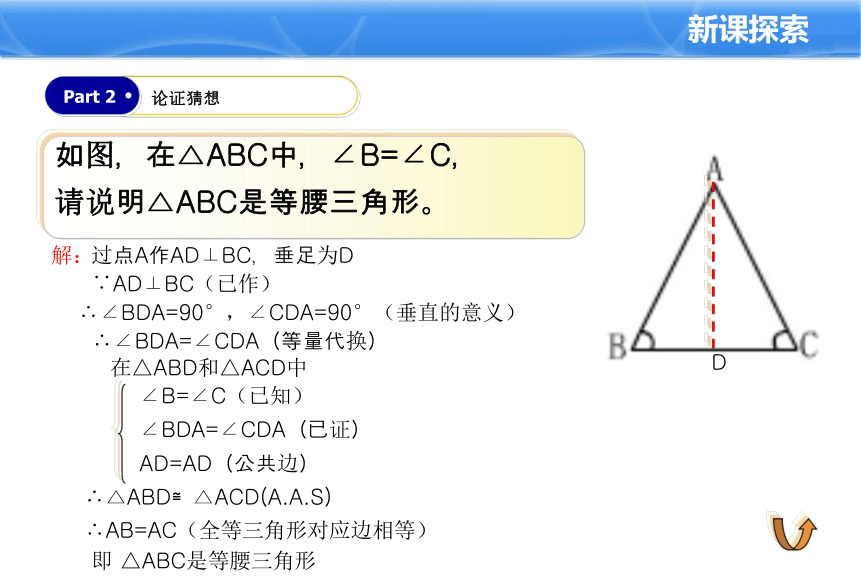
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
过点A作AD⊥BC,垂足为D
D
∵AD⊥BC(已作)
∴∠BDA=90°,∠CDA=90°(垂直的意义)
在△ABD和△ACD中
∠B=∠C(已知)
∠BDA=∠CDA(已证)
AD=AD(公共边)
∴△ABD≌△ACD(A.A.S)
∴AB=AC(全等三角形对应边相等)
即 △ABC是等腰三角形
∴∠BDA=∠CDA(等量代换)
新课探索
Part 1
Part 2
论证猜想
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
取BC的中点D,联结AD
D
∵点D是BD的中点(已作)
∴BD=DC(线段中点的意义)
思考:
还能继续证明下去吗?
新课探索
Part 1
Part 2
论证猜想
等腰三角形的判定方法:
如果一个三角形有两个角相等,
那么这两个角所对的边也相等,
这个三角形是等腰三角形。
(简称为“等角对等边”)
∵∠B=∠C
几何语言表达:
∴AB=AC(等角对等边)
即:△ABC是等腰三角形
概念辨析
Part 1
判断题
1、在△ABC中,如果∠A=∠B,那么△ABC是等腰三角形.( )
2、有两条边相等的三角形是等腰三角形. ( )
3、如果∠B=∠C,那么AB=AC. ( )
4、如果△ABC是等腰三角形,那么∠B=∠C. ( )
5、有两个底角相等的三角形是等腰三角形. ( )
V
V
X
X
X
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
我来解答!
小试牛刀
Part 1
Part 3
测试一
如图:已知∠A=36°?,∠DBC=36°,∠C=72°,
①∠1=_____度, ∠2=_____ 度。
③ 图中有____个等腰三角形,
分别是 __________
②如果AD=4cm,
则BC=_________ cm
④过D点作DE∥BC,图中
还有等腰三角形吗?为什么?
A
B
D
c
1
2
小试牛刀
art 1
Part 3
测试二
如图: ∠CAD是三角形ABC的外角,
(1)若∠1=∠2,AE∥BC。试问AB = AC吗?
(2)若AB = AC,AE∥BC,说明∠1=∠2的理由
A
E
C
B
D
1
2
等腰三角形的性质与判定有区别吗?
性质:等边 等角
判定:等角 等边
巩固提升
如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
且∠1=∠2 ,
说明△ABC是等腰三角形的理由。
变式:如上图,如果点D、E分别是AB、
AC上的点,BE=CD,且∠1=∠2.
试说明△ABC是等腰三角形的理由
总结反思
想判定一个三角形是等腰三角形,你有些什么方法?
1、根据等腰三角形的定义:两边相等
2、等腰三角形的判定:两内角相等
思考题1
A
B
如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?
C1
C2
C3
C4
2如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
等腰三角形的判定
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
你能解答吗?
情境引新
新课探索
Part 1
Part 2
论证猜想
如图,在△ABC中,
∠B=∠C,
请说明△ABC是等腰三角形。
只有这一种方法吗?
新课探索
Part 1
Part 2
论证猜想
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
过点A作∠A的角平分线,交BC于点D
D
∵AD是∠A的角平分线(已作)
∴∠BAD=∠CAD(角平分线的意义)
在△ABD和△ACD中
∠B=∠C(已知)
∠BAD=∠CAD(已证)
AD=AD(公共边)
∴△ABD≌△ACD(A.A.S)
∴AB=AC(全等三角形对应边相等)
即 △ABC是等腰三角形
新课探索
Part 1
Part 2
论证猜想
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
过点A作AD⊥BC,垂足为D
D
∵AD⊥BC(已作)
∴∠BDA=90°,∠CDA=90°(垂直的意义)
在△ABD和△ACD中
∠B=∠C(已知)
∠BDA=∠CDA(已证)
AD=AD(公共边)
∴△ABD≌△ACD(A.A.S)
∴AB=AC(全等三角形对应边相等)
即 △ABC是等腰三角形
∴∠BDA=∠CDA(等量代换)
新课探索
Part 1
Part 2
论证猜想
如图,在△ABC中,∠B=∠C,
请说明△ABC是等腰三角形。
解:
取BC的中点D,联结AD
D
∵点D是BD的中点(已作)
∴BD=DC(线段中点的意义)
思考:
还能继续证明下去吗?
新课探索
Part 1
Part 2
论证猜想
等腰三角形的判定方法:
如果一个三角形有两个角相等,
那么这两个角所对的边也相等,
这个三角形是等腰三角形。
(简称为“等角对等边”)
∵∠B=∠C
几何语言表达:
∴AB=AC(等角对等边)
即:△ABC是等腰三角形
概念辨析
Part 1
判断题
1、在△ABC中,如果∠A=∠B,那么△ABC是等腰三角形.( )
2、有两条边相等的三角形是等腰三角形. ( )
3、如果∠B=∠C,那么AB=AC. ( )
4、如果△ABC是等腰三角形,那么∠B=∠C. ( )
5、有两个底角相等的三角形是等腰三角形. ( )
V
V
X
X
X
A
B
O
如图,位于在海上A、B两处的两艘救生船接到O处的遇险报警,当时测得∠A=∠B。如果这两艘救生船以同样的速度同时出发,能不能大约同时赶到出事地点(不考虑风浪因素)?
我来解答!
小试牛刀
Part 1
Part 3
测试一
如图:已知∠A=36°?,∠DBC=36°,∠C=72°,
①∠1=_____度, ∠2=_____ 度。
③ 图中有____个等腰三角形,
分别是 __________
②如果AD=4cm,
则BC=_________ cm
④过D点作DE∥BC,图中
还有等腰三角形吗?为什么?
A
B
D
c
1
2
小试牛刀
art 1
Part 3
测试二
如图: ∠CAD是三角形ABC的外角,
(1)若∠1=∠2,AE∥BC。试问AB = AC吗?
(2)若AB = AC,AE∥BC,说明∠1=∠2的理由
A
E
C
B
D
1
2
等腰三角形的性质与判定有区别吗?
性质:等边 等角
判定:等角 等边
巩固提升
如图,在△ABC中,
已知BD、CE分别是AC、AB上的高,
且∠1=∠2 ,
说明△ABC是等腰三角形的理由。
变式:如上图,如果点D、E分别是AB、
AC上的点,BE=CD,且∠1=∠2.
试说明△ABC是等腰三角形的理由
总结反思
想判定一个三角形是等腰三角形,你有些什么方法?
1、根据等腰三角形的定义:两边相等
2、等腰三角形的判定:两内角相等
思考题1
A
B
如图,线段AB的端点B在直线 上(AB与直线 不垂直),请在直线 上另找一点C,使ΔABC为等腰三角形,这样的点能找几个?你能说出它们的画法吗?
C1
C2
C3
C4
2如图,把一张矩形的纸沿对角线折叠,重合部分是一个等腰三角形吗?为什么?
