人教版九年级数学上册24.1.1圆课件(共19张ppt)
文档属性
| 名称 | 人教版九年级数学上册24.1.1圆课件(共19张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览



文档简介
24.1 圆的有关性质
第二十四章 圆
24.1.1 圆
观察与思考
观察下列生活中的图片,找一找你所熟悉的图形.
·
r
O
A
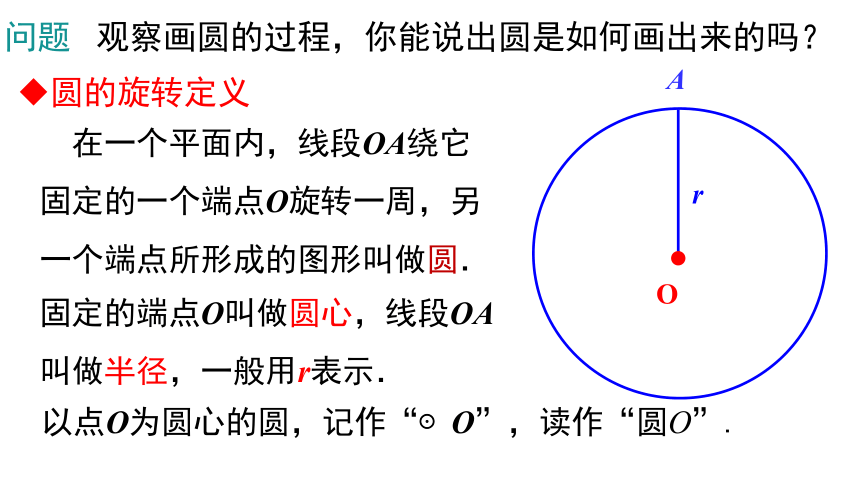
圆的旋转定义
问题 观察画圆的过程,你能说出圆是如何画出来的吗?
在一个平面内,线段OA绕它
固定的一个端点O旋转一周,另
一个端点所形成的图形叫做圆.
固定的端点O叫做圆心,线段OA
叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
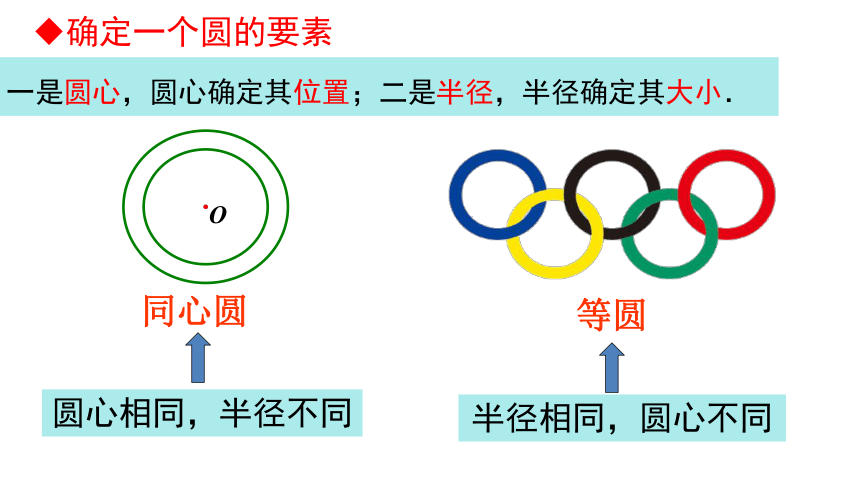
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
O
同心圆
等圆
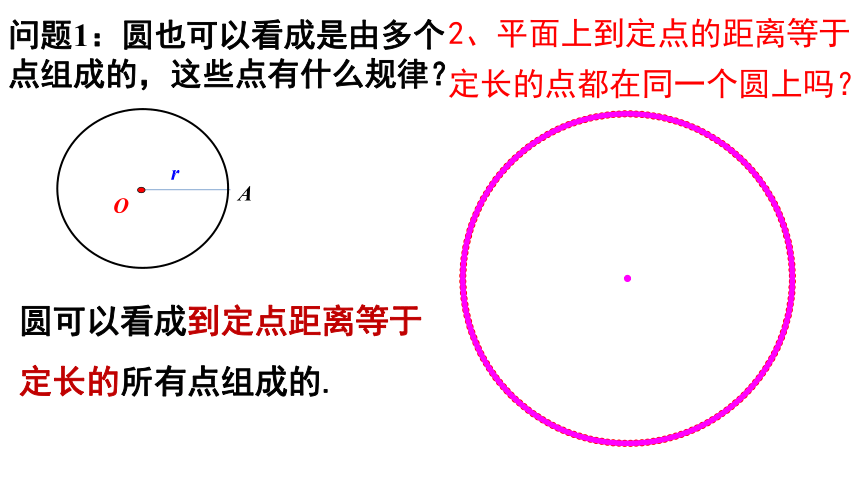
圆可以看成到定点距离等于
定长的所有点组成的.
2、平面上到定点的距离等于定长的点都在同一个圆上吗?
·
r
O
A
问题1:圆也可以看成是由多个
点组成的,这些点有什么规律?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
圆的集合定义
想一想:从画圆的过程可以看出什么呢?
同圆半径相等
圆的基本性质
典例精析
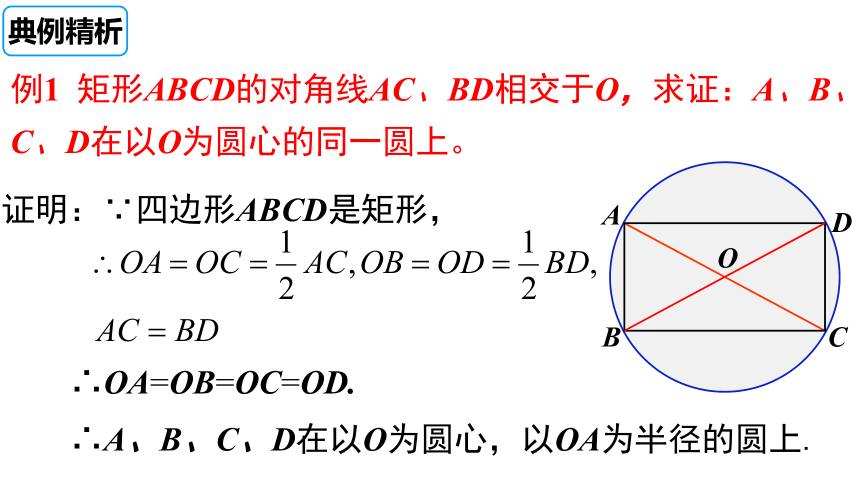
例1 矩形ABCD的对角线AC、BD相交于O,求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
弦:
·
C
O
A
B
注意
圆的有关概念
二
连接圆上任意两点的线段(如图中的AC)叫做弦.
特别地,经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段。
2.直径是弦,是经过圆心的特殊弦,但弦不一定是直径。
A
B
C
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
【发现】直径是最长的弦
弧:
O
A
B
:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
半圆
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
B
等圆:
·
C
O
A
·
C
O1
A
容易看出:等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
想一想:长度相等的弧是等弧吗?
“等弧”要区别于“长度相等的弧”
结论:等弧仅仅存在于同圆或者等圆中.
能够重合的两个圆叫做等圆.
例2 如图.
(1)请写出以点A为端点的优弧及劣弧;
弦AF,AB,AC,AD.其中弦AD是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 、 .
劣弧:
优弧:
AF,
(
AE,
(
AB,
(
AC.
(
AFC,
(
AFB,
(
ADE,
(
ADF.
(
AF
(
(2)请写出以点A为端点的弦及直径.
A
B
C
D
E
F
ADF
(
练习、判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
例3 如图,MN是半圆O的直径,正方形ABCD的顶点A、D在半圆上,顶点B、C在直径MN上,求证:OB=OC.
Ⅰ
Ⅱ
练习、设在例3中,⊙O的半径为10,则正方形ABCD的边长为 .
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
当堂练习
A
B
C
D
O
F
E
2.如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,
求∠ACD的度数。
.
3.如图,已知OA、OB为⊙O的半径,C、D分别为
OA、OB的中点,求证:AD=BC.
x
x
x
x
4、如图,在扇形MON中, ,半径MO=NO=10,正方形ABCD的顶点B、C、D在半径上,顶点A在圆弧上,求正方形ABCD的边长.
圆
定义
旋转定义
要画一个确定的圆,
关键是确定圆心和半径
集合定义
同圆半径相等
有关概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
课堂小结
第二十四章 圆
24.1.1 圆
观察与思考
观察下列生活中的图片,找一找你所熟悉的图形.
·
r
O
A
圆的旋转定义
问题 观察画圆的过程,你能说出圆是如何画出来的吗?
在一个平面内,线段OA绕它
固定的一个端点O旋转一周,另
一个端点所形成的图形叫做圆.
固定的端点O叫做圆心,线段OA
叫做半径,一般用r表示.
以点O为圆心的圆,记作“⊙O”,读作“圆O”.
一是圆心,圆心确定其位置;二是半径,半径确定其大小.
半径相同,圆心不同
圆心相同,半径不同
确定一个圆的要素
O
同心圆
等圆
圆可以看成到定点距离等于
定长的所有点组成的.
2、平面上到定点的距离等于定长的点都在同一个圆上吗?
·
r
O
A
问题1:圆也可以看成是由多个
点组成的,这些点有什么规律?
(1)圆上各点到定点(圆心O)的距离都等于 .
(2)到定点的距离等于定长的点都在 .
圆心为O、半径为r的圆可以看成是所有到定点O的距离等于定长r的点的集合.
O
·
A
C
E
r
r
r
r
r
D
定长r
同一个圆上
圆的集合定义
想一想:从画圆的过程可以看出什么呢?
同圆半径相等
圆的基本性质
典例精析
例1 矩形ABCD的对角线AC、BD相交于O,求证:A、B、C、D在以O为圆心的同一圆上。
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴OA=OB=OC=OD.
∴A、B、C、D在以O为圆心,以OA为半径的圆上.
弦:
·
C
O
A
B
注意
圆的有关概念
二
连接圆上任意两点的线段(如图中的AC)叫做弦.
特别地,经过圆心的弦(如图中的AB)叫做直径.
1.弦和直径都是线段。
2.直径是弦,是经过圆心的特殊弦,但弦不一定是直径。
A
B
C
O
A
B
O
A
B
探索:圆中最长的弦是什么?为什么?
O
A
B
C
C
D
C
D
【发现】直径是最长的弦
弧:
O
A
B
:圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫做半圆.
劣弧与优弧
·
C
O
A
半圆
小于半圆的弧叫做劣弧.如图中的AC ;
(
大于半圆的弧叫做优弧.如图中的ABC.
(
B
等圆:
·
C
O
A
·
C
O1
A
容易看出:等圆是两个半径相等的圆.
等弧:
在同圆或等圆中,能够互相重合的弧叫做等弧.
想一想:长度相等的弧是等弧吗?
“等弧”要区别于“长度相等的弧”
结论:等弧仅仅存在于同圆或者等圆中.
能够重合的两个圆叫做等圆.
例2 如图.
(1)请写出以点A为端点的优弧及劣弧;
弦AF,AB,AC,AD.其中弦AD是直径.
(3)请任选一条弦,写出这条弦所对的弧.
答案不唯一,如:弦AF,它所对的弧是 、 .
劣弧:
优弧:
AF,
(
AE,
(
AB,
(
AC.
(
AFC,
(
AFB,
(
ADE,
(
ADF.
(
AF
(
(2)请写出以点A为端点的弦及直径.
A
B
C
D
E
F
ADF
(
练习、判断下列说法的正误,并说明理由或举反例.
(1)弦是直径;
(2)半圆是弧;
(3)过圆心的线段是直径;
(4)过圆心的直线是直径;
(5)半圆是最长的弧;
(6)直径是最长的弦;
(7)长度相等的弧是等弧.
例3 如图,MN是半圆O的直径,正方形ABCD的顶点A、D在半圆上,顶点B、C在直径MN上,求证:OB=OC.
Ⅰ
Ⅱ
练习、设在例3中,⊙O的半径为10,则正方形ABCD的边长为 .
1.填空:
(1)______是圆中最长的弦,它是______的2倍.
(2)图中有 条直径, 条非直径的弦,
以A为一个端点的优弧有 条,劣弧有 条.
直径
半径
一
二
四
四
当堂练习
A
B
C
D
O
F
E
2.如图,在△ABC中,∠ACB=90°,∠A=40°;以C为圆心、CB为半径的圆交AB于点D,
求∠ACD的度数。
.
3.如图,已知OA、OB为⊙O的半径,C、D分别为
OA、OB的中点,求证:AD=BC.
x
x
x
x
4、如图,在扇形MON中, ,半径MO=NO=10,正方形ABCD的顶点B、C、D在半径上,顶点A在圆弧上,求正方形ABCD的边长.
圆
定义
旋转定义
要画一个确定的圆,
关键是确定圆心和半径
集合定义
同圆半径相等
有关概念
弦(直径)
直径是圆中最长的弦
弧
半圆是特殊的弧
劣弧
半圆
优弧
同心圆
等圆
同圆
等弧
课堂小结
同课章节目录
