人教版七年级数学下册课件:5.1.3 同位角、内错角、同旁内角(共22张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件:5.1.3 同位角、内错角、同旁内角(共22张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览



文档简介
第五章 相交线与平行线
5.1.3 同位角、内错角、同旁内角
知识回顾
两条直线相交,只有一个交点,产生四个角,如图:直线AB与CD相交于点O,得到∠1,∠2,∠3,∠4,在这些角中,哪些是相等的?哪些是互补的?
3
2
2
1
3
4
1
4
C
D
E
F
1
3
4
2
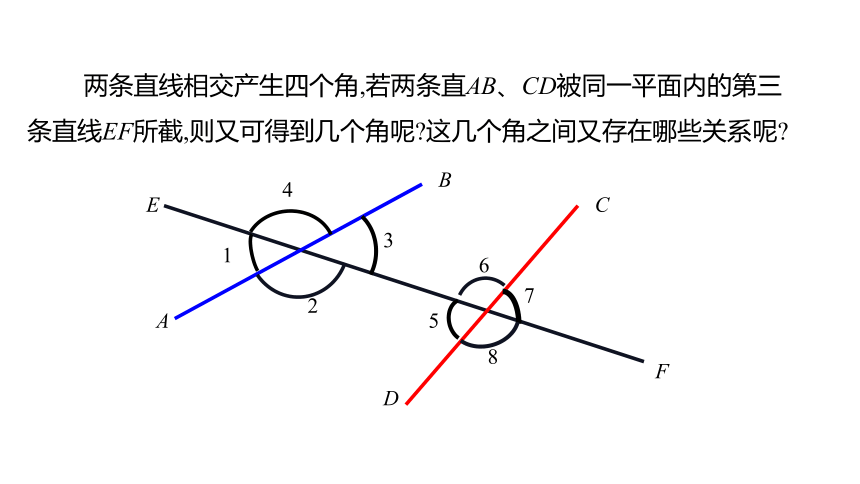
两条直线相交产生四个角,若两条直AB、CD被同一平面内的第三条直线EF所截,则又可得到几个角呢?这几个角之间又存在哪些关系呢?
6
7
5
8
B
A
F
E
C
D
4
3
1
2
获取新知
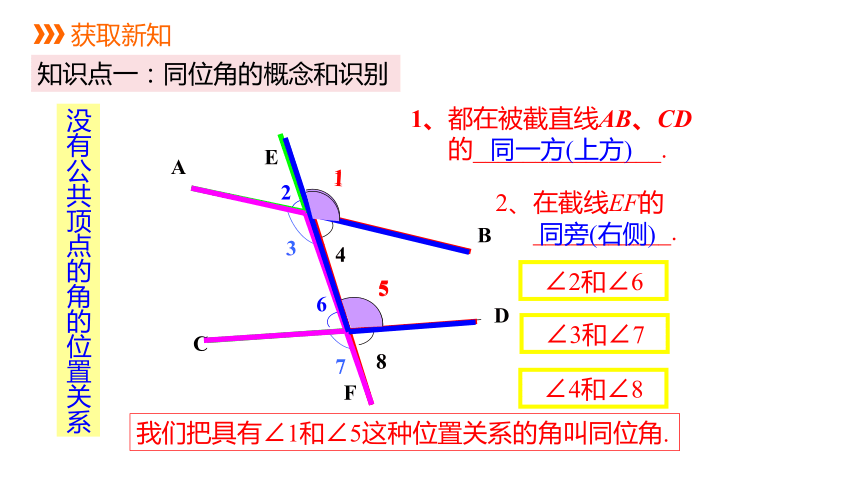
知识点一:同位角的概念和识别
A
B
C
D
F
2
3
6
7
8
4
1
5
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
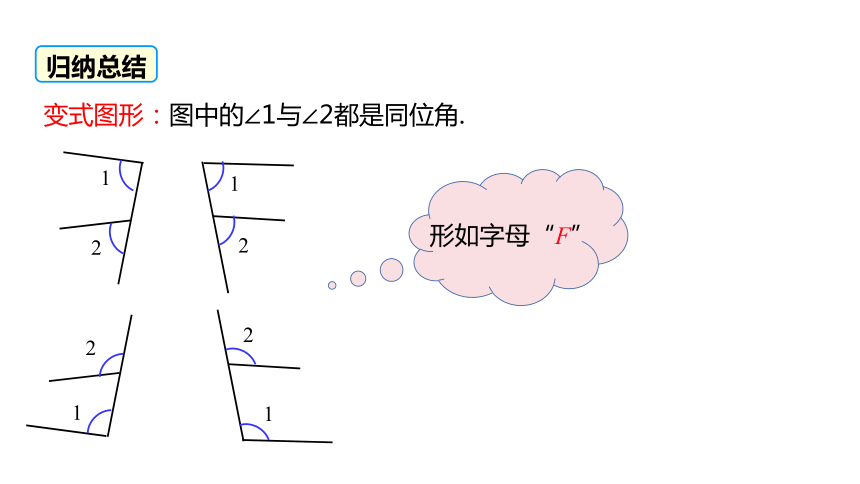
变式图形:图中的∠1与∠2都是同位角.
归纳总结
1
2
1
2
1
2
1
2
形如字母“F”
例题讲解
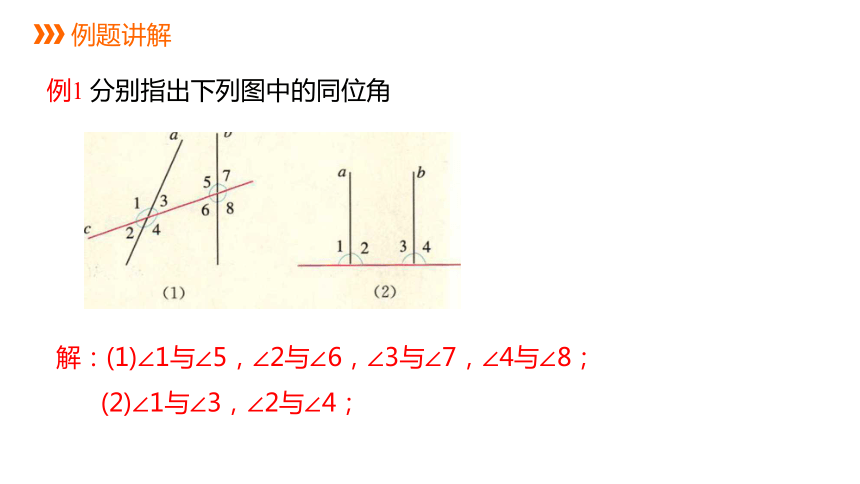
例1 分别指出下列图中的同位角
解:(1)∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
(2)∠1与∠3,∠2与∠4;
获取新知
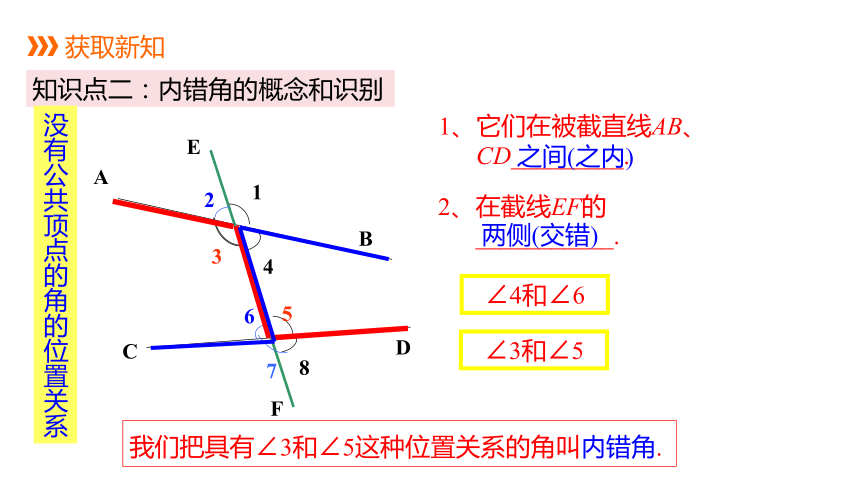
知识点二:内错角的概念和识别
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
1、它们在被截直线AB、
CD_________.
2、在截线EF的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
之间(之内)
∠4和∠6
∠3和∠5
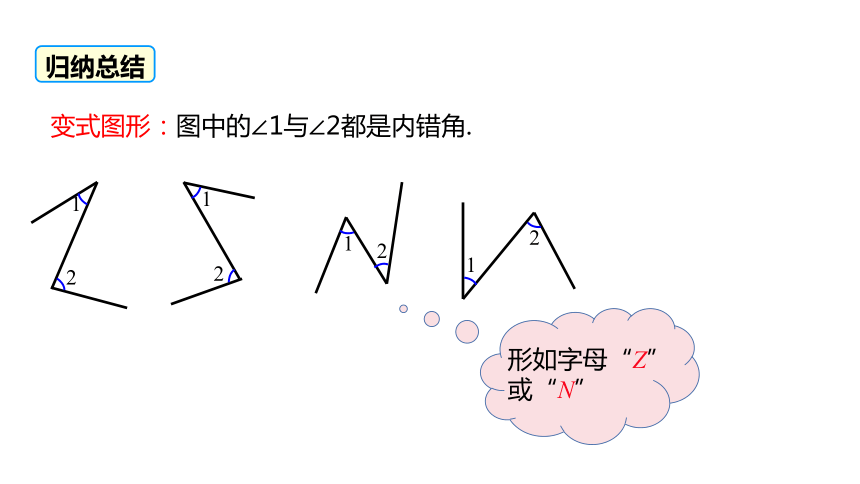
变式图形:图中的∠1与∠2都是内错角.
归纳总结
1
2
1
1
1
2
2
2
形如字母“Z”或“N”
例题讲解
例2 如图,试找出图中与∠2是同位角、内错角的角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
获取新知
知识点三:同旁内角的概念和识别
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
2、在截线EF的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
1、它们在两条被截直线AB、
CD_____________.
∠4和∠5
∠3和∠6
变式图形:图中的∠1与∠2都是同旁内角.
1
1
1
1
2
2
2
2
归纳总结
形如字母“U”
例题讲解
例3 如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,∠1和∠4是同位角.
4
3
2
1
F
E
D
C
B
A
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,
所以∠1+∠3=180°,即∠1与∠3互补.
随堂演练
1. 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3
C
2. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
3. 如图,与∠1互为同旁内角的角共有( )个.
A.1
B.2
C.3
D.4
C
4. 同位角的特征是在两条被截线的________,并且在截线的______,如图,∠_____和∠_____是同位角.
同一方
同侧
1
2
5. 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是________.
内错角
6. 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
E
D
C
B
A
8
7
6
5
4
3
2
1
解:两条直线是AB,AC,截线DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
7. 如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论.
A
B
C
D
E
解:∠B与∠BAD是内错角,∠B与∠BAE是同旁内角,它们都是直线BC,DE被直线AB所截形成的.
∠C与∠CAE是内错角,∠C与∠CAD是同旁内角,它们都是直线BC,DE被直线AC所截形成的.
另外,∠B与∠C是同旁内角,它们是直线AB,AC被直线BC所截形成的.
∠B与∠BAC是同旁内角,它们是直线AC,BC被直线AB所截形成的 .
∠C与∠BAC是同旁内角,它们是直线AB,BC被直线AC所截形成的.
A
B
C
D
E
课堂小结
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型或“N”型
同旁内角 “U”型
同位角
内错角
同旁内角
2.生活中的数学:三线八角手势记忆法
5.1.3 同位角、内错角、同旁内角
知识回顾
两条直线相交,只有一个交点,产生四个角,如图:直线AB与CD相交于点O,得到∠1,∠2,∠3,∠4,在这些角中,哪些是相等的?哪些是互补的?
3
2
2
1
3
4
1
4
C
D
E
F
1
3
4
2
两条直线相交产生四个角,若两条直AB、CD被同一平面内的第三条直线EF所截,则又可得到几个角呢?这几个角之间又存在哪些关系呢?
6
7
5
8
B
A
F
E
C
D
4
3
1
2
获取新知
知识点一:同位角的概念和识别
A
B
C
D
F
2
3
6
7
8
4
1
5
没有公共顶点的角的位置关系
E
1、都在被截直线AB、CD
的_______________.
2、在截线EF的
___________.
同一方(上方)
同旁(右侧)
∠2和∠6
∠3和∠7
∠4和∠8
1
5
我们把具有∠1和∠5这种位置关系的角叫同位角.
变式图形:图中的∠1与∠2都是同位角.
归纳总结
1
2
1
2
1
2
1
2
形如字母“F”
例题讲解
例1 分别指出下列图中的同位角
解:(1)∠1与∠5,∠2与∠6,∠3与∠7,∠4与∠8;
(2)∠1与∠3,∠2与∠4;
获取新知
知识点二:内错角的概念和识别
A
B
C
D
E
F
2
7
6
4
没有公共顶点的角的位置关系
1、它们在被截直线AB、
CD_________.
2、在截线EF的
___________.
1
8
3
5
两侧(交错)
我们把具有∠3和∠5这种位置关系的角叫内错角.
之间(之内)
∠4和∠6
∠3和∠5
变式图形:图中的∠1与∠2都是内错角.
归纳总结
1
2
1
1
1
2
2
2
形如字母“Z”或“N”
例题讲解
例2 如图,试找出图中与∠2是同位角、内错角的角.
解: ∠2的同位角为∠6,∠2的内错角为∠8.
获取新知
知识点三:同旁内角的概念和识别
A
B
C
D
E
F
2
7
6
没有公共顶点的角的位置关系
2、在截线EF的
____________.
1
8
4
5
3
6
之间(之内)
同一旁(同侧)
我们把具有∠3和∠6这种位置关系的角叫同旁内角.
1、它们在两条被截直线AB、
CD_____________.
∠4和∠5
∠3和∠6
变式图形:图中的∠1与∠2都是同旁内角.
1
1
1
1
2
2
2
2
归纳总结
形如字母“U”
例题讲解
例3 如图,直线DE,BC被直线AB所截.
(1)∠1和∠2, ∠1和∠3, ∠1和∠4 各是什么位置关系的角?
(2) 如果∠1=∠4,那么∠1和∠2相等吗?
∠1和∠3互补吗?为什么?
4
3
2
1
F
E
D
C
B
A
解:(1)∠1与∠2是内错角,
∠1和∠3同旁内角,∠1和∠4是同位角.
4
3
2
1
F
E
D
C
B
A
解:(2)如果∠1=∠4,由对顶角相等,得∠2=∠4,那么∠1=∠2.因为∠3和∠4互补,即∠4+∠3=180°,又因为∠1=∠4,
所以∠1+∠3=180°,即∠1与∠3互补.
随堂演练
1. 如图,在所标识的角中,同位角是( )
A.∠1和∠2 B.∠1和∠3
C.∠1和∠4 D.∠2和∠3
C
2. 在我们常见的英文字母中,也存在着同位角、内错角、同旁内角,在下面几个字母中,含有内错角最少的字母是( )
C
3. 如图,与∠1互为同旁内角的角共有( )个.
A.1
B.2
C.3
D.4
C
4. 同位角的特征是在两条被截线的________,并且在截线的______,如图,∠_____和∠_____是同位角.
同一方
同侧
1
2
5. 如图,两只手的食指和大拇指在同一个平面内,它们构成的一对角可看成是________.
内错角
6. 如图,直线DE截AB ,AC,构成8个角,指出所有的同位角,内错角,同旁内角.
E
D
C
B
A
8
7
6
5
4
3
2
1
解:两条直线是AB,AC,截线DE,所以8个角中,
同位角:∠2与∠5,∠4与∠7,∠1与∠8, ∠6和∠3;
内错角:∠4与∠5,∠1与∠6;
同旁内角:∠1与∠5,∠4与∠6.
7. 如图,∠B与哪个角是内错角,与哪个角是同旁内角?它们分别是哪两条直线被哪一条直线所截形成的?对∠C进行同样的讨论.
A
B
C
D
E
解:∠B与∠BAD是内错角,∠B与∠BAE是同旁内角,它们都是直线BC,DE被直线AB所截形成的.
∠C与∠CAE是内错角,∠C与∠CAD是同旁内角,它们都是直线BC,DE被直线AC所截形成的.
另外,∠B与∠C是同旁内角,它们是直线AB,AC被直线BC所截形成的.
∠B与∠BAC是同旁内角,它们是直线AC,BC被直线AB所截形成的 .
∠C与∠BAC是同旁内角,它们是直线AB,BC被直线AC所截形成的.
A
B
C
D
E
课堂小结
1.同位角、内错角、同旁内角的结构特征:
三线八角
同位角 “F”型
内错角 “Z”型或“N”型
同旁内角 “U”型
同位角
内错角
同旁内角
2.生活中的数学:三线八角手势记忆法
