人教版七年级数学下册课件:5.2.1 平行线(21张PPT)
文档属性
| 名称 | 人教版七年级数学下册课件:5.2.1 平行线(21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览







文档简介
第五章 相交线与平行线
5.2.1 平行线
知识回顾
问题 前面我们学的两条不重合的直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?下面我们一起来观察图片体会一下.
情景导入
扶手
双杠
铁轨
跑道
泳池
扶梯
获取新知
知识点一:平行线的概念及表示
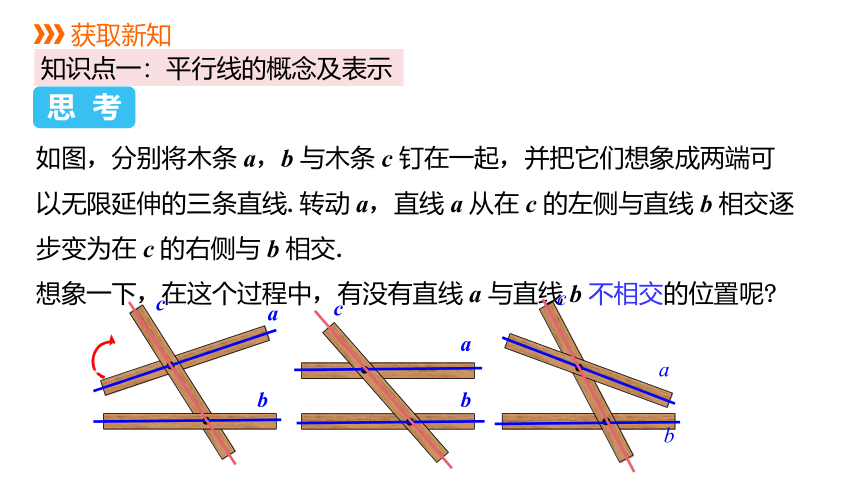
如图,分别将木条 a,b 与木条 c 钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动 a,直线 a 从在 c 的左侧与直线 b 相交逐步变为在 c 的右侧与 b 相交.
想象一下,在这个过程中,有没有直线 a 与直线 b 不相交的位置呢?
思 考
a
b
c
a
b
c
a
b
c
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
a
b
在同一平面内,
不重合的两条直线只有两种位置关系:相交和平行.
例题讲解
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,而不是“线段”.
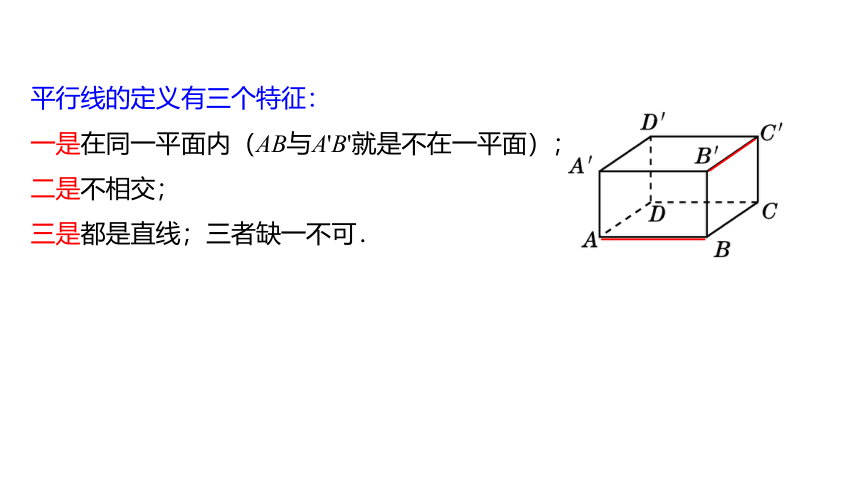
平行线的定义有三个特征:
一是在同一平面内(AB与A'B'就是不在一平面);
二是不相交;
三是都是直线;三者缺一不可.
获取新知
知识点二:平行线的画法
思 考
在之前转动木条 a 的过程中,有几个位置使得直线 a 与 b 平行?如图,过点 B 画直线 a 的平行线,能画出几条?再过点 C 画直线 a 的平行线,它和前面过点 B 画出的直线平行吗?
a
B
C
(1)放
(2)靠
(3)推
(4)画
归纳总结
通过观察和画图,可以发现一个基本事实(平行公理):
经过直线外一点,有且只有一条直线与这条直线平行.
·
A
·
B
·
·
C
D
a
b
例题讲解
例2 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过P点向右画射线PN∥BC交AC于点N;(2)在(1)中画出的图形中,∠MPN的度数一定等于180°,你能说明其中的道理吗?
A
B
C
P
解:(1)画出的射线PM,PN,如图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°.
由平行公理,进一步可以得到如下结论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
几何语言表达:
因为a//c , c//b(已知)
所以a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
获取新知
知识点三:平行线的传递性质
a
b
c
随堂演练
1. 下列生活实例中:①交通道口的斑马线;②天上的彩虹;
③体操的纵队;④长方形门框的上下边;⑤火车的平直铁轨线.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
4. 如图,当风车的一片叶子AB旋转到与地面MN平行时,叶子CD所在的直线与地面MN________,理由是_________
__________________________________________.
相交
经过直线
外一点,有且只有一条直线与这条直线平行
5.如图,在长方体的各条棱中,与AB平行的有_______________,与AB相交的有__________________,与AB既不平行又不相交的有________________________.
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
6.如图,直线a//b,b∥c,c∥d,
那么a ∥d 吗?为什么?
a
b
c
d
解:因为 a ∥b,b∥c,所以 a ∥c
(如果两条直线都与第三条直线平行,那么这两条直线互相平行).
因为 c∥d,所以 a ∥d
(如果两条直线都与第三条直线平行,那么这两条直线互相平行).
课堂小结
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直
线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
5.2.1 平行线
知识回顾
问题 前面我们学的两条不重合的直线具有怎样位置关系?
两条直线相交(其中垂直是相交的特殊情形)
生活中两条直线除了相交以外,还有什么情形呢?下面我们一起来观察图片体会一下.
情景导入
扶手
双杠
铁轨
跑道
泳池
扶梯
获取新知
知识点一:平行线的概念及表示
如图,分别将木条 a,b 与木条 c 钉在一起,并把它们想象成两端可以无限延伸的三条直线.转动 a,直线 a 从在 c 的左侧与直线 b 相交逐步变为在 c 的右侧与 b 相交.
想象一下,在这个过程中,有没有直线 a 与直线 b 不相交的位置呢?
思 考
a
b
c
a
b
c
a
b
c
在木条转动过程中,存在一条直线a与直线b不相交的情形,这时我们说直线a与b互相平行.记作“a∥b”.
在同一平面内,不相交的两条直线叫做平行线.
a
b
在同一平面内,
不重合的两条直线只有两种位置关系:相交和平行.
例题讲解
例1 判断下列说法是否正确,并说明理由.
(1)不相交的两条直线是平行线;
(2)在同一平面内,两条不相交的线段是平行线.
解:(1)不正确;
理由:根据定义,它缺少了“在同一平面内”这一条件.
(2)不正确;
理由:定义中指出的是两条不相交的“直线”,而不是“线段”.
平行线的定义有三个特征:
一是在同一平面内(AB与A'B'就是不在一平面);
二是不相交;
三是都是直线;三者缺一不可.
获取新知
知识点二:平行线的画法
思 考
在之前转动木条 a 的过程中,有几个位置使得直线 a 与 b 平行?如图,过点 B 画直线 a 的平行线,能画出几条?再过点 C 画直线 a 的平行线,它和前面过点 B 画出的直线平行吗?
a
B
C
(1)放
(2)靠
(3)推
(4)画
归纳总结
通过观察和画图,可以发现一个基本事实(平行公理):
经过直线外一点,有且只有一条直线与这条直线平行.
·
A
·
B
·
·
C
D
a
b
例题讲解
例2 如图,P是三角形ABC内部的任意一点.
(1)过P点向左画射线PM∥BC交AB于点M,过P点向右画射线PN∥BC交AC于点N;(2)在(1)中画出的图形中,∠MPN的度数一定等于180°,你能说明其中的道理吗?
A
B
C
P
解:(1)画出的射线PM,PN,如图.
(2)因为射线PM∥BC,射线PN∥BC,
所以直线PM∥BC,直线PN∥BC.
所以直线PM与直线PN是同一条直线(过直线外一
点有且只有一条直线与这条直线平行),
即点M, P, N在同一条直线上.所以∠MPN=180°.
由平行公理,进一步可以得到如下结论:
如果两条直线都与第三条直线平行,那么这两条直线也互相平行.
几何语言表达:
因为a//c , c//b(已知)
所以a//b(如果两条直线都和第三条直线平行,那么这两条直线也互相平行).
获取新知
知识点三:平行线的传递性质
a
b
c
随堂演练
1. 下列生活实例中:①交通道口的斑马线;②天上的彩虹;
③体操的纵队;④长方形门框的上下边;⑤火车的平直铁轨线.其中属于平行线的有( )
A.1个 B.2个 C.3个 D.4个
D
2.已知直线AB和一点P,过点P画直线AB的平行线,可画( )
A.1条 B.0条
C.1条或0条 D.无数条
C
3.下列推理正确的是( )
A.因为a // d,b // c,所以c // d
B.因为a // c,b // d,所以c // d
C.因为a // b,a // c,所以b // c
D.因为a // b,c // d,所以a // c
C
4. 如图,当风车的一片叶子AB旋转到与地面MN平行时,叶子CD所在的直线与地面MN________,理由是_________
__________________________________________.
相交
经过直线
外一点,有且只有一条直线与这条直线平行
5.如图,在长方体的各条棱中,与AB平行的有_______________,与AB相交的有__________________,与AB既不平行又不相交的有________________________.
CD、A1B1、C1D1
A1A、B1B、AD、BC
A1D1、B1C1、D1D、C1C
6.如图,直线a//b,b∥c,c∥d,
那么a ∥d 吗?为什么?
a
b
c
d
解:因为 a ∥b,b∥c,所以 a ∥c
(如果两条直线都与第三条直线平行,那么这两条直线互相平行).
因为 c∥d,所以 a ∥d
(如果两条直线都与第三条直线平行,那么这两条直线互相平行).
课堂小结
1.在同一平面内,不相交的两条直线叫做平行线.
3.如果两条直线都与第三条直线平行,那么这两条直
线互相平行.
2.经过直线外一点,有且只有一条直线与已知直线平行.
