人教版七年级数学下册课件:5.2.2 平行线的判定(共24张ppt)
文档属性
| 名称 | 人教版七年级数学下册课件:5.2.2 平行线的判定(共24张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 19:27:24 | ||
图片预览





文档简介
第五章 相交线与平行线
5.2.2 平行线的判定
知识回顾
问题1 同一平面内,两条不重合的直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 还记的学过的平行线的性质吗?
相交(包括垂直)和平行两种.
运用定义来判断(很难操作)
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.经过直线外一点,有且只有一条直线与已知直线平行.
获取新知
知识点一:利用同位角判定两直线平行
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行.
那么,有没有其他判定方法呢?
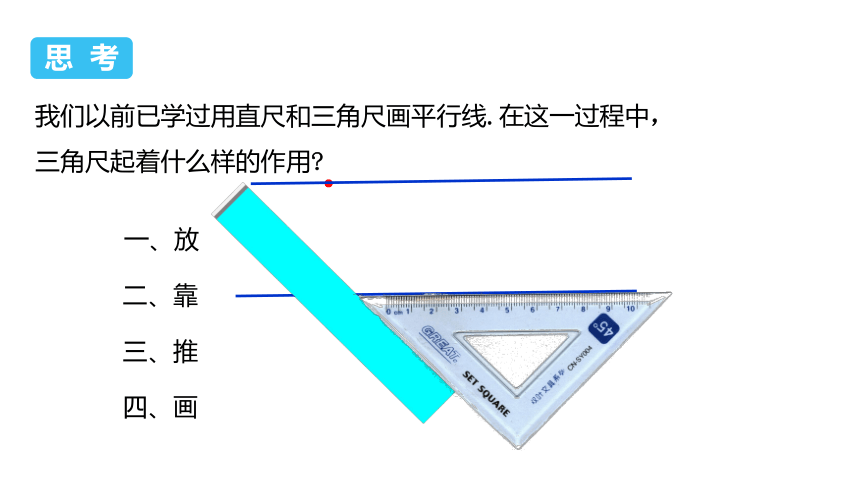
思 考
我们以前已学过用直尺和三角尺画平行线.在这一过程中,
三角尺起着什么样的作用?
●
一、放
二、靠
三、推
四、画
b
A
2
1
a
B
1
2
a
b
A
B
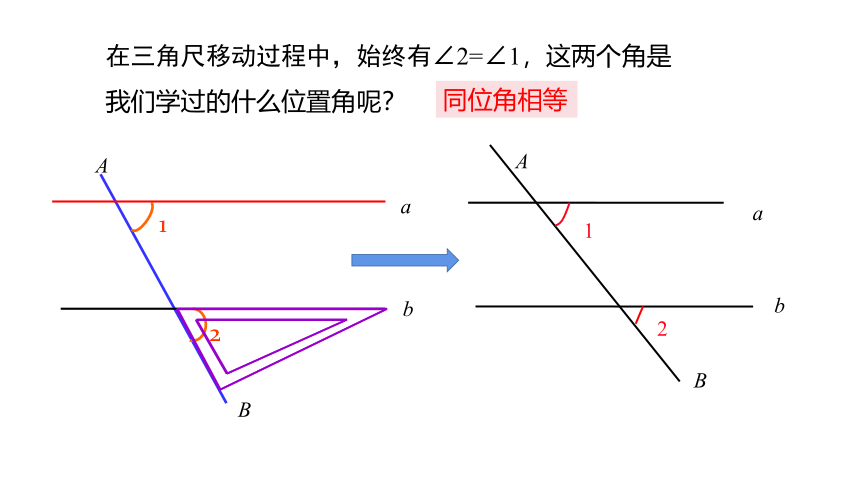
在三角尺移动过程中,始终有∠2=∠1,这两个角是我们学过的什么位置角呢?
同位角相等
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
符号语言:
∵∠1=∠2,(已知)
∴l1∥l2.
(同位角相等,两直线平行)
1
2
a
b
c
B
总结归纳
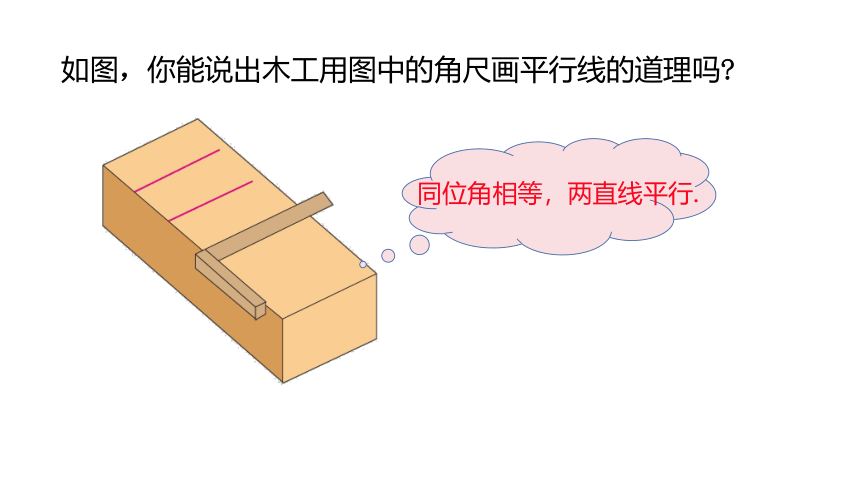
如图,你能说出木工用图中的角尺画平行线的道理吗?
同位角相等,两直线平行.
例题讲解
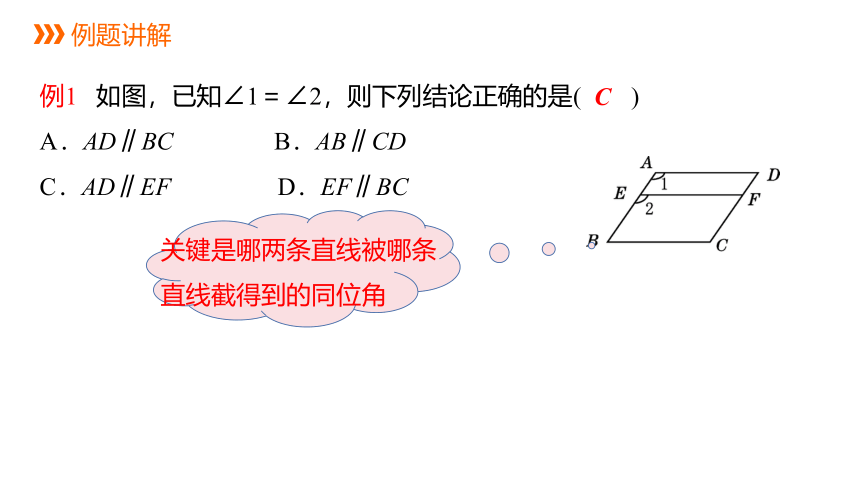
例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
C
关键是哪两条直线被哪条直线截得到的同位角
获取新知
知识点二:利用内错角判定两直线平行
思 考
两条直线被第三条直线所载,同时得到同位角、内错角和同旁内角.由同位角相等,可以判定两条直线平行,那么能否利用内错角,或同旁内角来判定两条直线平行呢?
如图,如果∠2=∠3,能得出a∥b吗?
分析:因为∠2=∠3,
而∠3=∠1(对顶角相等),
所以∠1=∠2,即同位角相等,
从而a∥b.
1
2
3
4
a
b
c
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b.(内错角相等,两直线平行)
符号语言:
总结归纳
2
b
a
1
c
例题讲解
例2 如图,BE是AB的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C可以判定哪两条直线平行? 根据是什么?
解:(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
A
B
C
D
E
获取新知
知识点三:利用同旁内角判定两直线平行
如图,如果∠1+∠2=180°,能得出a∥b吗?
分析:因为∠1+∠2=180°,
而∠1+∠4=180°(平角定义),
所以∠1=∠2,即同位角相等,
从而a∥b.
4
2
3
1
a
b
c
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°,(已知)
∴a∥b.(同旁内角互补,两直线平行)
总结归纳
2
b
a
1
c
例题讲解
例3 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
1
2
a
b
c
答:这两条直线平行.理由如下:
∵ b⊥a,
∴∠1=90°.
同理 ∠2=90°.
∴∠1=∠2.
∵∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
符号“∵”表示“因为”,
符号“∴”表示“所以”.
1
2
a
b
c
还有其他的方法吗?
随堂演练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
1
2
3
A
E
B
C
D
C
2.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐150?,第二次向左拐30?
B.第一次向左拐30?,第二次向右拐30?
C.第一次向右拐130?,第二次向右拐50?
D.第一次向左拐150?,第二次向左拐30?
B
4. (1)如图,若∠1=∠2,则 ∥ ;
若∠2=∠3,则 ∥ .
(2)如图,若∠1=∠2,则 ∥ ;
若∠3=∠4,则 ∥ .
AB
DE
BC
EF
AD
BC
AB
CD
5. 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?为什么?
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
A
B
D
C
E
F
G
A
B
D
C
E
F
G
解: (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
6. 如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
F
D
C
A
B
E
1
2
解:不能.∠1与∠2不是一组内错角.
添加∠CBD=∠EDB.
∵∠1=∠2,
∠CBD=∠EDB,
∴∠ABD=∠FDB,
∴AB∥DF.(内错角相等,两直线平行)
课堂小结
判定两条直线平行的方法
文字叙述
符号语言
图形
相等,
两直线平行
∵ ,(已知)
∴a∥b
_ __相等,
两直线平行
∵ ,(已知)
∴a∥b
_________互补,
两直线平行
∵ ,(已知)
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
5.2.2 平行线的判定
知识回顾
问题1 同一平面内,两条不重合的直线的位置关系有哪几种?
问题2 怎样的两条直线平行?
问题3 还记的学过的平行线的性质吗?
相交(包括垂直)和平行两种.
运用定义来判断(很难操作)
2.如果两条直线都与第三条直线平行,那么这两条直线互相平行.
1.经过直线外一点,有且只有一条直线与已知直线平行.
获取新知
知识点一:利用同位角判定两直线平行
根据平行线的定义,如果平面内的两条直线不相交,就可以判断这两条直线平行.
但是,由于直线无限延伸,检验它们是否相交有困难,所以难以直接根据定义来判断两条直线是否平行.
那么,有没有其他判定方法呢?
思 考
我们以前已学过用直尺和三角尺画平行线.在这一过程中,
三角尺起着什么样的作用?
●
一、放
二、靠
三、推
四、画
b
A
2
1
a
B
1
2
a
b
A
B
在三角尺移动过程中,始终有∠2=∠1,这两个角是我们学过的什么位置角呢?
同位角相等
判定方法1:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.
简单说成:同位角相等,两直线平行.
符号语言:
∵∠1=∠2,(已知)
∴l1∥l2.
(同位角相等,两直线平行)
1
2
a
b
c
B
总结归纳
如图,你能说出木工用图中的角尺画平行线的道理吗?
同位角相等,两直线平行.
例题讲解
例1 如图,已知∠1=∠2,则下列结论正确的是( )
A.AD∥BC B.AB∥CD
C.AD∥EF D.EF∥BC
C
关键是哪两条直线被哪条直线截得到的同位角
获取新知
知识点二:利用内错角判定两直线平行
思 考
两条直线被第三条直线所载,同时得到同位角、内错角和同旁内角.由同位角相等,可以判定两条直线平行,那么能否利用内错角,或同旁内角来判定两条直线平行呢?
如图,如果∠2=∠3,能得出a∥b吗?
分析:因为∠2=∠3,
而∠3=∠1(对顶角相等),
所以∠1=∠2,即同位角相等,
从而a∥b.
1
2
3
4
a
b
c
判定方法2:两条直线被第三条直线所截 ,如果内错角相等,那么这两条直线平行.
简单说成:内错角相等,两直线平行.
∵∠1=∠2,(已知)
∴a∥b.(内错角相等,两直线平行)
符号语言:
总结归纳
2
b
a
1
c
例题讲解
例2 如图,BE是AB的延长线.
(1)由∠CBE= ∠A 可以判定哪两条直线平行? 根据是什么?
(2)由∠CBE= ∠C可以判定哪两条直线平行? 根据是什么?
解:(1)由∠CBE=∠A可以判定AD∥BC.
根据是:同位角相等,两直线平行.
(2)由∠CBE=∠C可以判定AB∥CD.
根据是:内错角相等,两直线平行.
A
B
C
D
E
获取新知
知识点三:利用同旁内角判定两直线平行
如图,如果∠1+∠2=180°,能得出a∥b吗?
分析:因为∠1+∠2=180°,
而∠1+∠4=180°(平角定义),
所以∠1=∠2,即同位角相等,
从而a∥b.
4
2
3
1
a
b
c
判定方法3:两条直线被第三条直线所截 ,如果同旁内角互补,那么这两条直线平行.
简单说成:同旁内角互补,两直线平行.
符号语言:
∵∠1+∠2=180°,(已知)
∴a∥b.(同旁内角互补,两直线平行)
总结归纳
2
b
a
1
c
例题讲解
例3 在同一平面内,如果两条直线都垂直于同一条直线,那么这两条直线平行吗?为什么?
分析:垂直总与直角联系在一起,进而用判断两条直线平行的方法进行判定.
1
2
a
b
c
答:这两条直线平行.理由如下:
∵ b⊥a,
∴∠1=90°.
同理 ∠2=90°.
∴∠1=∠2.
∵∠1和∠2是同位角,
∴b∥c(同位角相等,两直线平行).
符号“∵”表示“因为”,
符号“∴”表示“所以”.
1
2
a
b
c
还有其他的方法吗?
随堂演练
1.如图,可以确定AB∥CE的条件是( )
A.∠2=∠B B. ∠1=∠A
C. ∠3=∠B D. ∠3=∠A
1
2
3
A
E
B
C
D
C
2.如图,下列说法错误的是( )
A.若a∥b,b∥c,则a∥c
B.若∠1=∠2,则a∥c
C.若∠3=∠2,则b∥c
D.若∠3+∠4=180°,则a∥c
C
3.一学员在广场上练习驾驶汽车,两次拐弯后,行驶
方向与原来相同,这两次拐弯的角度可能是( )
A.第一次向右拐150?,第二次向左拐30?
B.第一次向左拐30?,第二次向右拐30?
C.第一次向右拐130?,第二次向右拐50?
D.第一次向左拐150?,第二次向左拐30?
B
4. (1)如图,若∠1=∠2,则 ∥ ;
若∠2=∠3,则 ∥ .
(2)如图,若∠1=∠2,则 ∥ ;
若∠3=∠4,则 ∥ .
AB
DE
BC
EF
AD
BC
AB
CD
5. 如图,E是AB上一点,F是DC上一点,G是BC延长线上一点.
(1)如果∠B=∠DCG,可以判断哪两条直线平行?为什么?
(2)如果∠D=∠DCG,可以判断哪两条直线平行?为什么?
(3)如果∠D+∠DFE=180°,可以判断哪两条直线平行?为什么?
A
B
D
C
E
F
G
A
B
D
C
E
F
G
解: (1)AB//CD, 同位角相等,两直线平行;
(2)AD//BC, 内错角相等,两直线平行;
(3)AD//EF, 同旁内角互补,两直线平行.
6. 如图,∠1=∠2,能判断AB∥DF吗?为什么?
若不能判断AB∥DF,你认为还需要再添加的一个条件是什么呢?写出这个条件,并说明你的理由.
F
D
C
A
B
E
1
2
解:不能.∠1与∠2不是一组内错角.
添加∠CBD=∠EDB.
∵∠1=∠2,
∠CBD=∠EDB,
∴∠ABD=∠FDB,
∴AB∥DF.(内错角相等,两直线平行)
课堂小结
判定两条直线平行的方法
文字叙述
符号语言
图形
相等,
两直线平行
∵ ,(已知)
∴a∥b
_ __相等,
两直线平行
∵ ,(已知)
∴a∥b
_________互补,
两直线平行
∵ ,(已知)
∴a∥b
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
a
b
c
1
2
4
3
