人教版数学八年级上册15.1.2分式的基本性质 课件(共18张ppt)
文档属性
| 名称 | 人教版数学八年级上册15.1.2分式的基本性质 课件(共18张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 518.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览






文档简介
15.1.2分式的基本性质
学习目标
理解分式的基本性质
能运用分式的基本性质对分式进行变形
类比归纳,得到性质
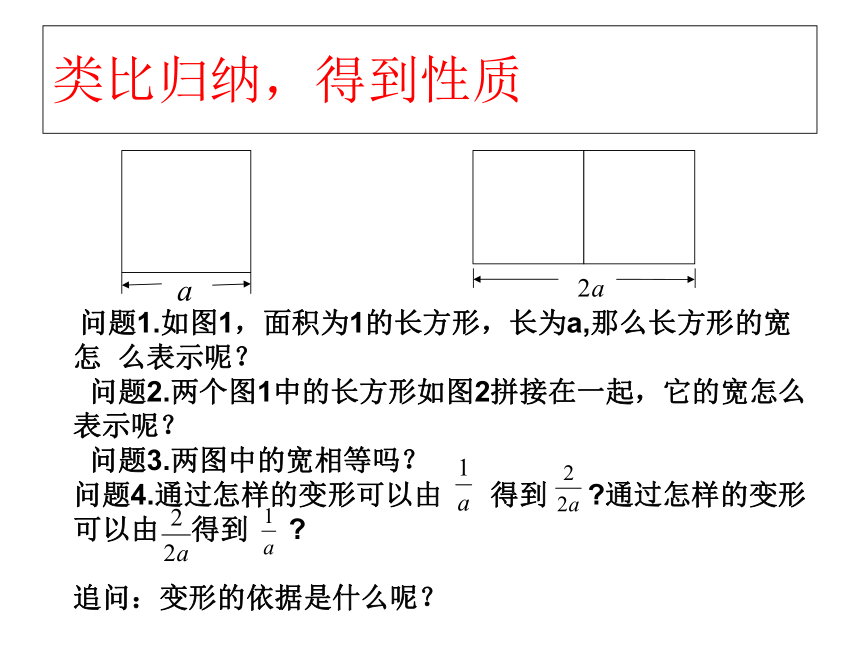
问题1.如图1,面积为1的长方形,长为a,那么长方形的宽怎 么表示呢?
问题2.两个图1中的长方形如图2拼接在一起,它的宽怎么表示呢?
问题3.两图中的宽相等吗?
问题4.通过怎样的变形可以由 得到 ?通过怎样的变形可以由 得到 ?
追问:变形的依据是什么呢?
类比归纳,得到性质
问题5.若n个这样的长方形拼接在一起?它的宽又如何表示呢?
追问: 和 、 相等吗?通过怎样的变形可以得到他们相等呢?
问题6.若(m+1)个这样的长方形拼接在一起,宽又如何表示呢?
追问: 和 、 相等吗?通过怎样的变形可以得到他们相等呢?
问题7. 能类比分数的基本性质,归纳出分式的基本性质吗?
分式的基本性质
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
问题8.你能尝试用符号语言表示分式的基本性质吗?
A,B,C都为整式 (C≠0)
运用性质,进行变形
例1 判断下列从左到右的变形是否正确?
(1)
(2)
(3)
(4)
正确
错误
错误
正确
共同归纳,记心间
应用分式基本性质对分式进行变形需要注意的问题:
1.分子、分母应同时做乘,除法中的同一种变换;
2.所乘或除以的必须是同一个整式;
3.所乘或除以的整式应该不等于零.
练习
例2 填空(在括号内填入适当的整式,使分式值不变)
例3 填空(在括号内填入适当的整式,使分式值不变)
巩固练习,加深理解
【基础训练】
填空(1)
(2)
(3)
巩固练习,加深理解
【拓展训练】
若将分式 (a,b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值( )
A. 扩大为原来的2倍 B. 缩小为原来的
C. 不改变 D. 缩小为原来的
B
齐来做游戏
游戏“找朋友”:一组卡片上标记分式(出现的字母均不为零)
每组第一位学生是评委,其他每人手中有一张卡片.
游戏规则:任选一人上台展示他的分式,其他同学的分式若与他的相等即为朋友,评委裁决正误并看本组有无人未找到朋友.
我们来小结:
本节课学习的内容
(1)分式的基本性质 ( 均为整式,且 )
(2)分式的基本性质的作用:分式进行变形的依据
2. 运用基本性质需要注意的问题;
课后思考
不改变分式的值,将分母和分子的首项不含 “-”号
当堂达标
1.下列式子从左到右变形正确的是( )
A B. C. D.
2.填空 (1) (2)
3.把分式 的分子、分母中的x,y同时扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.缩小2倍 D.无法确定
布置作业
必做题
选做题
习题15.1 第4题
习题15.1第5题
学习目标
理解分式的基本性质
能运用分式的基本性质对分式进行变形
类比归纳,得到性质
问题1.如图1,面积为1的长方形,长为a,那么长方形的宽怎 么表示呢?
问题2.两个图1中的长方形如图2拼接在一起,它的宽怎么表示呢?
问题3.两图中的宽相等吗?
问题4.通过怎样的变形可以由 得到 ?通过怎样的变形可以由 得到 ?
追问:变形的依据是什么呢?
类比归纳,得到性质
问题5.若n个这样的长方形拼接在一起?它的宽又如何表示呢?
追问: 和 、 相等吗?通过怎样的变形可以得到他们相等呢?
问题6.若(m+1)个这样的长方形拼接在一起,宽又如何表示呢?
追问: 和 、 相等吗?通过怎样的变形可以得到他们相等呢?
问题7. 能类比分数的基本性质,归纳出分式的基本性质吗?
分式的基本性质
分式的分子与分母都乘以(或除以)同一个不等于零的整式,分式的值不变.
问题8.你能尝试用符号语言表示分式的基本性质吗?
A,B,C都为整式 (C≠0)
运用性质,进行变形
例1 判断下列从左到右的变形是否正确?
(1)
(2)
(3)
(4)
正确
错误
错误
正确
共同归纳,记心间
应用分式基本性质对分式进行变形需要注意的问题:
1.分子、分母应同时做乘,除法中的同一种变换;
2.所乘或除以的必须是同一个整式;
3.所乘或除以的整式应该不等于零.
练习
例2 填空(在括号内填入适当的整式,使分式值不变)
例3 填空(在括号内填入适当的整式,使分式值不变)
巩固练习,加深理解
【基础训练】
填空(1)
(2)
(3)
巩固练习,加深理解
【拓展训练】
若将分式 (a,b均为正数)中的字母a、b的值分别扩大为原来的2倍,则分式的值( )
A. 扩大为原来的2倍 B. 缩小为原来的
C. 不改变 D. 缩小为原来的
B
齐来做游戏
游戏“找朋友”:一组卡片上标记分式(出现的字母均不为零)
每组第一位学生是评委,其他每人手中有一张卡片.
游戏规则:任选一人上台展示他的分式,其他同学的分式若与他的相等即为朋友,评委裁决正误并看本组有无人未找到朋友.
我们来小结:
本节课学习的内容
(1)分式的基本性质 ( 均为整式,且 )
(2)分式的基本性质的作用:分式进行变形的依据
2. 运用基本性质需要注意的问题;
课后思考
不改变分式的值,将分母和分子的首项不含 “-”号
当堂达标
1.下列式子从左到右变形正确的是( )
A B. C. D.
2.填空 (1) (2)
3.把分式 的分子、分母中的x,y同时扩大2倍,则分式的值( )
A.不变 B.扩大2倍 C.缩小2倍 D.无法确定
布置作业
必做题
选做题
习题15.1 第4题
习题15.1第5题
