苏科版数学八年级上册6.4 用一次函数解决问题 课件(共16张ppt)
文档属性
| 名称 | 苏科版数学八年级上册6.4 用一次函数解决问题 课件(共16张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:01:15 | ||
图片预览


文档简介
用一次函数解决问题
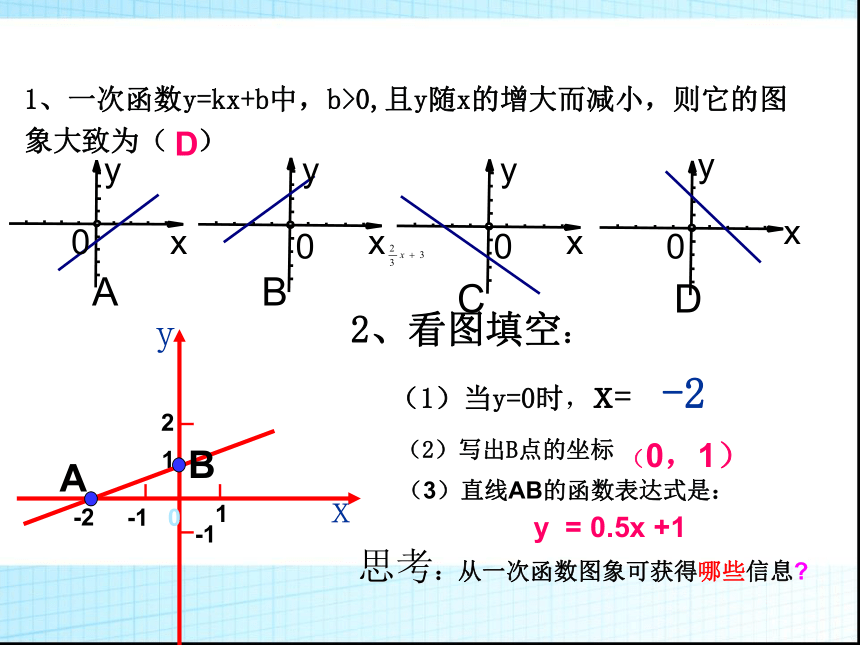
1、一次函数y=kx+b中,b>0,且y随x的增大而减小,则它的图象大致为( )
D
C
B
A
x
y
0
x
x
x
y
y
y
0
0
0
D
-2
2
0
1
2、看图填空:
1
-1
-2
-1
(1)当y=0时,x=
(2)写出B点的坐标
x
y
(3)直线AB的函数表达式是:
y = 0.5x +1
A
B
(0,1)
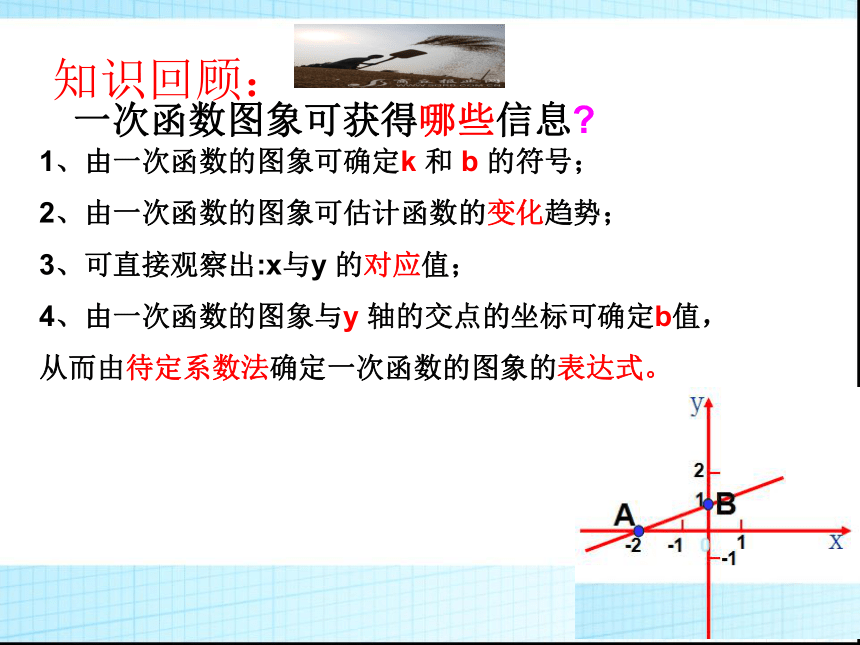
思考:从一次函数图象可获得哪些信息?
知识回顾:
1、由一次函数的图象可确定k 和 b 的符号;
2、由一次函数的图象可估计函数的变化趋势;
3、可直接观察出:x与y 的对应值;
4、由一次函数的图象与y 轴的交点的坐标可确定b值,
从而由待定系数法确定一次函数的图象的表达式。
一次函数图象可获得哪些信息?
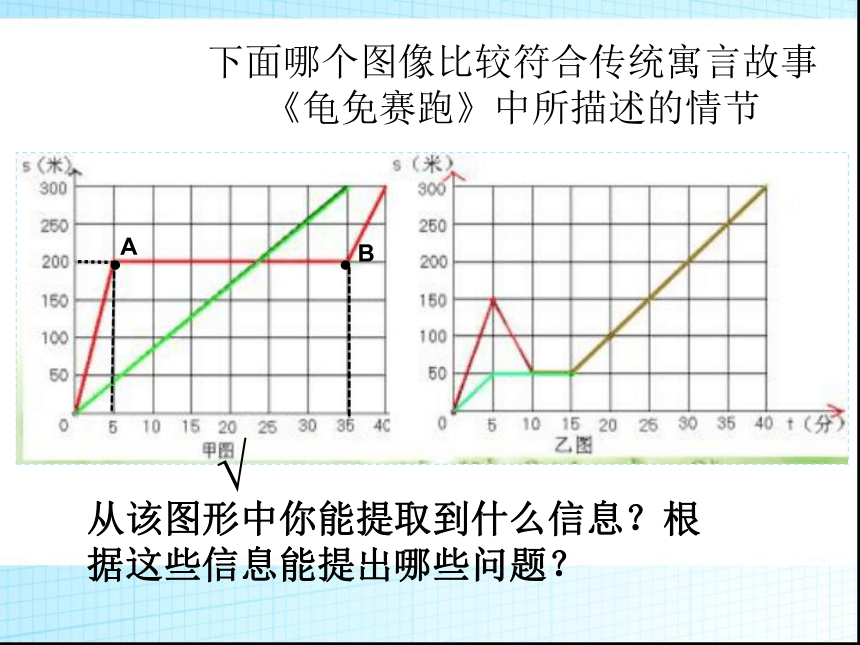
下面哪个图像比较符合传统寓言故事
《龟免赛跑》中所描述的情节
从该图形中你能提取到什么信息?根据这些信息能提出哪些问题?
√
A
B
如何解答实际情景函数图象的信息?
1:理解横纵坐标分别表示的的实际意义
2:分析已知(看已知的是自变量还是因变量),
通过做x轴或y轴的垂线,在图象上找到对应的点,
由点的横坐标或者纵坐标的值读出要求的值
3: 利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
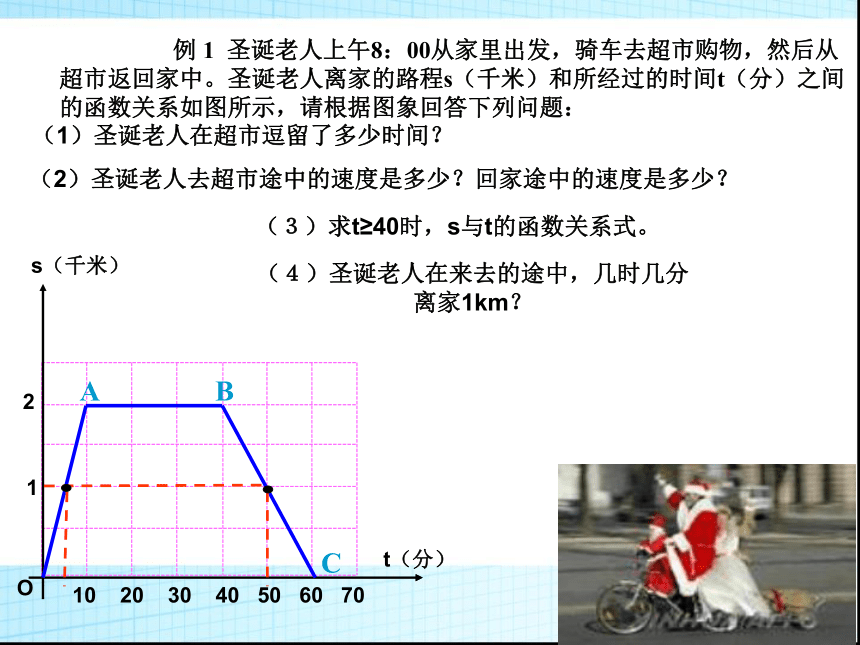
(2)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(1)圣诞老人在超市逗留了多少时间?
(4)圣诞老人在来去的途中,几时几分离家1km?
(3)求t≥40时,s与t的函数关系式。
例 1 圣诞老人上午8:00从家里出发,骑车去超市购物,然后从超市返回家中。圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
10 20 30 40 50 60 70
O
t(分)
s(千米)
1
2
A
C
B
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
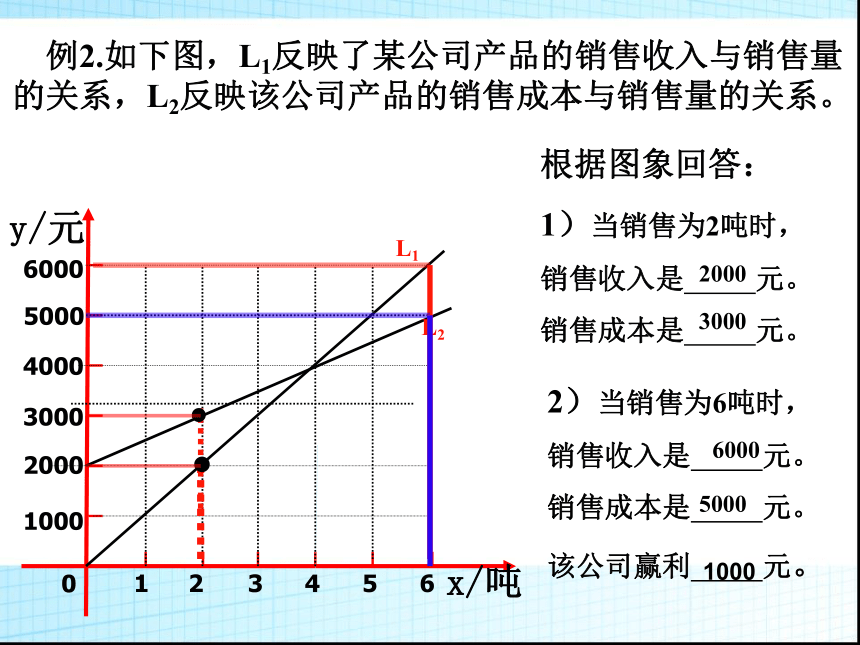
例2.如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
根据图象回答:
1)当销售为2吨时,
销售收入是 元。
销售成本是 元。
2)当销售为6吨时,
销售收入是 元。
销售成本是 元。
该公司赢利 元。
.
.
2000
3000
5000
6000
1000
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
根据图象回答:
3)当销售量为 时,
销售收入等于销售成本。
4)当销售量 时,
该公司赢利。
(即收入大于成本)。
当销售量 时,
该公司亏损
(即收入小于成本)。
例2.如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
.
4
大于4吨
小于4吨
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
根据图象回答:
例2. 如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
5)L1对应的函数表达
式为 。
L2对应的函数表达
式是 。
.
.
新龟兔赛跑
一次兔子全力以赴,
拿下了比赛!
乌龟
兔
下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。
想一想:
新龟兔赛跑
s (米)
(1)这一次是 米赛跑。
1
2
3
4
5
O
100
20
120
40
60
80
t (分)
6
8
7
(2)表示兔子的图象是 。
-1
12
9
10
11
-3
-2
l1
l2
100
l2
-4
根据图象,你能设计哪些问题?
s /米
(3)当兔子到达终点时,乌龟距终点还有 米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米。
(5)乌龟要先到达终点,至少要比兔子早跑 分钟。
-1
12
9
10
11
-3
-2
40
4
-4
40
2. 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量x的关系如图:
(1)旅客最多可免费携带多少千克行李?
⑵超过30千克后,行李票费用y元与行李质量x的关系式?
30
(3)当行李票费用 74 元时,旅客携带的行李质量为多少?
(3)求s>3时,y与s的函数关系式。
3.某市出租车计费方法如图所示,请根据图象回答下面的问题:
(1)出租车的起步价是多少元?在多少路程内只收起步价?
(2)起步价里程走完之后,每行驶1km需多少车费?
(4)某外地客人坐出租车游览本市,车费为31元,试求出他乘车的里程。
5元
3km
通过这节课的学习,你有什么收获?
1、知识方面:通过一次函数的图象获取相关 的信息;
3、数学能力:初步体会方程与函数的关系,增
强识图能力,应用能力。
2、数学思维:①数形结合,函数与方程的思想
②利用函数图像解决简单的实际问题
反思小结
作业:
1、一次函数y=kx+b中,b>0,且y随x的增大而减小,则它的图象大致为( )
D
C
B
A
x
y
0
x
x
x
y
y
y
0
0
0
D
-2
2
0
1
2、看图填空:
1
-1
-2
-1
(1)当y=0时,x=
(2)写出B点的坐标
x
y
(3)直线AB的函数表达式是:
y = 0.5x +1
A
B
(0,1)
思考:从一次函数图象可获得哪些信息?
知识回顾:
1、由一次函数的图象可确定k 和 b 的符号;
2、由一次函数的图象可估计函数的变化趋势;
3、可直接观察出:x与y 的对应值;
4、由一次函数的图象与y 轴的交点的坐标可确定b值,
从而由待定系数法确定一次函数的图象的表达式。
一次函数图象可获得哪些信息?
下面哪个图像比较符合传统寓言故事
《龟免赛跑》中所描述的情节
从该图形中你能提取到什么信息?根据这些信息能提出哪些问题?
√
A
B
如何解答实际情景函数图象的信息?
1:理解横纵坐标分别表示的的实际意义
2:分析已知(看已知的是自变量还是因变量),
通过做x轴或y轴的垂线,在图象上找到对应的点,
由点的横坐标或者纵坐标的值读出要求的值
3: 利用数形结合的思想:
将“数”转化为“形” 由“形”定“数”
(2)圣诞老人去超市途中的速度是多少?回家途中的速度是多少?
(1)圣诞老人在超市逗留了多少时间?
(4)圣诞老人在来去的途中,几时几分离家1km?
(3)求t≥40时,s与t的函数关系式。
例 1 圣诞老人上午8:00从家里出发,骑车去超市购物,然后从超市返回家中。圣诞老人离家的路程s(千米)和所经过的时间t(分)之间的函数关系如图所示,请根据图象回答下列问题:
10 20 30 40 50 60 70
O
t(分)
s(千米)
1
2
A
C
B
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
例2.如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
根据图象回答:
1)当销售为2吨时,
销售收入是 元。
销售成本是 元。
2)当销售为6吨时,
销售收入是 元。
销售成本是 元。
该公司赢利 元。
.
.
2000
3000
5000
6000
1000
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
根据图象回答:
3)当销售量为 时,
销售收入等于销售成本。
4)当销售量 时,
该公司赢利。
(即收入大于成本)。
当销售量 时,
该公司亏损
(即收入小于成本)。
例2.如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
.
4
大于4吨
小于4吨
x/吨
y/元
1000
2000
3000
4000
5000
6000
1
2
3
4
5
6
0
L1
L2
根据图象回答:
例2. 如下图,L1反映了某公司产品的销售收入与销售量的关系,L2反映该公司产品的销售成本与销售量的关系。
5)L1对应的函数表达
式为 。
L2对应的函数表达
式是 。
.
.
新龟兔赛跑
一次兔子全力以赴,
拿下了比赛!
乌龟
兔
下图 l1 l2 分别是龟兔赛跑中路程与时间之间的函数图象。
想一想:
新龟兔赛跑
s (米)
(1)这一次是 米赛跑。
1
2
3
4
5
O
100
20
120
40
60
80
t (分)
6
8
7
(2)表示兔子的图象是 。
-1
12
9
10
11
-3
-2
l1
l2
100
l2
-4
根据图象,你能设计哪些问题?
s /米
(3)当兔子到达终点时,乌龟距终点还有 米。
l1
l2
1
2
3
4
5
O
100
20
120
40
60
80
t /分
6
8
7
(4)乌龟要与兔子同时到达终点乌龟要先跑 米。
(5)乌龟要先到达终点,至少要比兔子早跑 分钟。
-1
12
9
10
11
-3
-2
40
4
-4
40
2. 某地长途汽车客运公司规定旅客可随身携带一定质量的行李,如果超过规定,则需要购买行李票,行李票费用y元与行李质量x的关系如图:
(1)旅客最多可免费携带多少千克行李?
⑵超过30千克后,行李票费用y元与行李质量x的关系式?
30
(3)当行李票费用 74 元时,旅客携带的行李质量为多少?
(3)求s>3时,y与s的函数关系式。
3.某市出租车计费方法如图所示,请根据图象回答下面的问题:
(1)出租车的起步价是多少元?在多少路程内只收起步价?
(2)起步价里程走完之后,每行驶1km需多少车费?
(4)某外地客人坐出租车游览本市,车费为31元,试求出他乘车的里程。
5元
3km
通过这节课的学习,你有什么收获?
1、知识方面:通过一次函数的图象获取相关 的信息;
3、数学能力:初步体会方程与函数的关系,增
强识图能力,应用能力。
2、数学思维:①数形结合,函数与方程的思想
②利用函数图像解决简单的实际问题
反思小结
作业:
同课章节目录
- 第一章 全等三角形
- 1.1 全等图形
- 1.2 全等三角形
- 1.3 探索三角形全等的条件
- 数学活动 关于三角形全等的条件
- 第二章 轴对称图形
- 2.1 轴对称与轴对称图形
- 2.2 轴对称的性质
- 2.3 设计轴对称图案
- 2.4 线段、角的轴对称性
- 2.5 等腰三角形的轴对称性
- 数学活动 折纸与证明
- 第三章 勾股定理
- 3.1 勾股定理
- 3.2 勾股定理的逆定理
- 3.3 勾股定理的简单应用
- 数学活动 探寻“勾股数”
- 第四章 实数
- 4.1 平方根
- 4.2 立方根
- 4.3 实数
- 4.4 近似数
- 数学活动 有关“实数”的课题探究
- 第五章 平面直角坐标系
- 5.1 物体位置的确定
- 5.2 平面直角坐标系
- 数学活动 确定藏宝地
- 第六章 一次函数
- 6.1 函数
- 6.2 一次函数
- 6.3 一次函数的图像
- 6.4 用一次函数解决问题
- 6.5 一次函数与二元一次方程
- 6.6 一次函数、一元一次方程和一元一次不等式
- 数学活动 温度计上的一次函数
