湘教版(2012)初中数学七年级上册 4.1 几何图形 课件(共34张ppt)
文档属性
| 名称 | 湘教版(2012)初中数学七年级上册 4.1 几何图形 课件(共34张ppt) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览











文档简介
4.1 几何图形
我们生活的世界里,充满了多姿多彩的图形,今天,让我们一起用数学的眼光来观察生活中的事物吧!
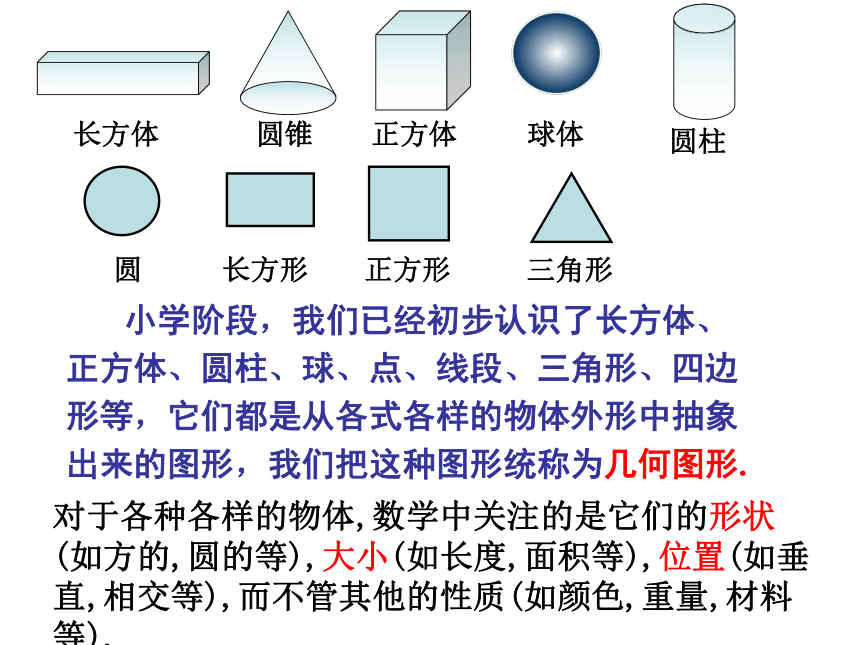
长方体
北京奥运“水立方”
圆柱体
圆锥
天坛
圆锥
圆柱体
上海“东方明珠”电视塔
球体
埃及金字塔
棱锥
请从下面事物中,说出你熟悉的图形——
球体
正方体
圆柱
长方体
圆锥
长方形
圆
正方形
三角形
小学阶段,我们已经初步认识了长方体、正方体、圆柱、球、点、线段、三角形、四边形等,它们都是从各式各样的物体外形中抽象出来的图形,我们把这种图形统称为几何图形.
对于各种各样的物体,数学中关注的是它们的形状(如方的,圆的等),大小(如长度,面积等),位置(如垂直,相交等),而不管其他的性质(如颜色,重量,材料等).
球体
正方体
圆柱
长方体
圆锥
长方形
圆
正方形
三角形
这些几何图形如何分类?分类的依据是什么?
几何图形:
(点,线,面,体)
立体图形:
各部分不都在同一个平面内.
平面图形:
各部分都在同一个平面内.
(例如,长方体、圆柱、圆锥、球等.)
(例如,点、线段、直线、三角形、长方形、圆等.)
按照各部分是否在同一平面内分类
看不同侧面,看到的是长方形或正方形;
如图,整体上看,我们看到的是长方体;
从长方形或正方形中,我们还可以看到点、线段.
长
方
体
长方形
正方形
点
线段
虽然立体图形与平面图形是两类不同的几何图形,但它们是相互联系的,立体图形中某些部分是平面图形,如正方体的每个侧面都是正方形.
点动成线
线动成面
直角三角形绕一条直角边旋转成圆锥体
面动成体
棱锥
圆锥
三棱锥
四棱锥
五棱锥
六棱锥
直立放置后,有一个多边形的底面,和一些共用一个顶点的三角形侧面等特征的立体图形称为棱锥。
如果它的底是n边形,我们就把它称为n棱锥。
棱柱
圆柱
五棱柱
四棱柱
正方体
长方体
六棱柱
三棱柱
直立放置后,具有:上下两个面大小、形状都相同,各侧面都是长方形等特征的立体图形称为棱柱。
如果它的底是n边形,我们就把它称为n棱柱。
小结
几何图形:
平面图形:
各部分都在同一个平面内.
立体图形:
各部分不都在同一个平面内.
平面图形与立体图形的联系
了解棱锥和棱柱
(1) (2) (3) (4) (5) (6)
你能把下列几何图形分成两类吗?
(A)
(B)
(C)
(D)
下列各图形,都是柱体的是( )
C
请你分别说出从下列实物中能抽象出的立体图形.
棱椎
长方体
球体
正方体
圆柱体
长方体
棱柱
图中的各立体图形的表面包含哪些平面图形?
下面纸片用透明胶粘贴后,是什么立体图形?
如图:第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体.用线连一连.
(1) (2) (3) (4) (5)
几何学的起源
土地测量
在古埃及,由于尼罗河经常泛滥而需要不断修整土地,重新划定边界,由此测量土地的方法引起人们的重视.几何学的英文单词geometry就是由geo(土地)和metry(测量)组成的.我国古代对形的研究也与测量关系密切,夏禹治水时期就有规、矩、准、绳等测量工具.约公元前1000年的西周初期,人们已经知道了直角三角形的“勾三,股四、弦五”的事实.大量事实说明,测量活动是几何学形成的直接原因.
随着时间的推移,人们在大量的实践中不断扩大和加深对形的认识,得到了许多关于形的知识和研究形的方法.约公元前300年,古希腊数学家
欧几里得广泛收集和研究前人的成果,将已有的关于数和形的知识作了系统编排,写成了《原本》一书,这是几何发展史上的一个里程碑.
几何学之父—欧几里得
七巧板(Tangram)起源于宋代,是我国人民创造的益智游戏,流传到世界上不少国家.?由一个正方形分割的七块几何形状可以拼出千变万化的几何图形,形似各种自然事物.近代围绕七巧板展开的科学研究证明七巧板的设计和人工智能、拓扑学之间有密切的联系.
1994年由香港承办的第35届国际数学奥林匹克的会标——一条乘风破浪的帆船。
我们生活的世界里,充满了多姿多彩的图形,今天,让我们一起用数学的眼光来观察生活中的事物吧!
长方体
北京奥运“水立方”
圆柱体
圆锥
天坛
圆锥
圆柱体
上海“东方明珠”电视塔
球体
埃及金字塔
棱锥
请从下面事物中,说出你熟悉的图形——
球体
正方体
圆柱
长方体
圆锥
长方形
圆
正方形
三角形
小学阶段,我们已经初步认识了长方体、正方体、圆柱、球、点、线段、三角形、四边形等,它们都是从各式各样的物体外形中抽象出来的图形,我们把这种图形统称为几何图形.
对于各种各样的物体,数学中关注的是它们的形状(如方的,圆的等),大小(如长度,面积等),位置(如垂直,相交等),而不管其他的性质(如颜色,重量,材料等).
球体
正方体
圆柱
长方体
圆锥
长方形
圆
正方形
三角形
这些几何图形如何分类?分类的依据是什么?
几何图形:
(点,线,面,体)
立体图形:
各部分不都在同一个平面内.
平面图形:
各部分都在同一个平面内.
(例如,长方体、圆柱、圆锥、球等.)
(例如,点、线段、直线、三角形、长方形、圆等.)
按照各部分是否在同一平面内分类
看不同侧面,看到的是长方形或正方形;
如图,整体上看,我们看到的是长方体;
从长方形或正方形中,我们还可以看到点、线段.
长
方
体
长方形
正方形
点
线段
虽然立体图形与平面图形是两类不同的几何图形,但它们是相互联系的,立体图形中某些部分是平面图形,如正方体的每个侧面都是正方形.
点动成线
线动成面
直角三角形绕一条直角边旋转成圆锥体
面动成体
棱锥
圆锥
三棱锥
四棱锥
五棱锥
六棱锥
直立放置后,有一个多边形的底面,和一些共用一个顶点的三角形侧面等特征的立体图形称为棱锥。
如果它的底是n边形,我们就把它称为n棱锥。
棱柱
圆柱
五棱柱
四棱柱
正方体
长方体
六棱柱
三棱柱
直立放置后,具有:上下两个面大小、形状都相同,各侧面都是长方形等特征的立体图形称为棱柱。
如果它的底是n边形,我们就把它称为n棱柱。
小结
几何图形:
平面图形:
各部分都在同一个平面内.
立体图形:
各部分不都在同一个平面内.
平面图形与立体图形的联系
了解棱锥和棱柱
(1) (2) (3) (4) (5) (6)
你能把下列几何图形分成两类吗?
(A)
(B)
(C)
(D)
下列各图形,都是柱体的是( )
C
请你分别说出从下列实物中能抽象出的立体图形.
棱椎
长方体
球体
正方体
圆柱体
长方体
棱柱
图中的各立体图形的表面包含哪些平面图形?
下面纸片用透明胶粘贴后,是什么立体图形?
如图:第二行的图形绕虚线旋转一周,便能形成第一行的某个几何体.用线连一连.
(1) (2) (3) (4) (5)
几何学的起源
土地测量
在古埃及,由于尼罗河经常泛滥而需要不断修整土地,重新划定边界,由此测量土地的方法引起人们的重视.几何学的英文单词geometry就是由geo(土地)和metry(测量)组成的.我国古代对形的研究也与测量关系密切,夏禹治水时期就有规、矩、准、绳等测量工具.约公元前1000年的西周初期,人们已经知道了直角三角形的“勾三,股四、弦五”的事实.大量事实说明,测量活动是几何学形成的直接原因.
随着时间的推移,人们在大量的实践中不断扩大和加深对形的认识,得到了许多关于形的知识和研究形的方法.约公元前300年,古希腊数学家
欧几里得广泛收集和研究前人的成果,将已有的关于数和形的知识作了系统编排,写成了《原本》一书,这是几何发展史上的一个里程碑.
几何学之父—欧几里得
七巧板(Tangram)起源于宋代,是我国人民创造的益智游戏,流传到世界上不少国家.?由一个正方形分割的七块几何形状可以拼出千变万化的几何图形,形似各种自然事物.近代围绕七巧板展开的科学研究证明七巧板的设计和人工智能、拓扑学之间有密切的联系.
1994年由香港承办的第35届国际数学奥林匹克的会标——一条乘风破浪的帆船。
同课章节目录
