湘教版八年级数学下册课件:3.2 简单图形的坐标表示(共19张ppt)
文档属性
| 名称 | 湘教版八年级数学下册课件:3.2 简单图形的坐标表示(共19张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 525.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览






文档简介
第3章 图形与坐标
3.2 简单图形的坐标表示
问题 正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
情景导入
(1)如果以点B为原点,以BC所在直线为x轴,建立平面直角坐标系,那么y轴是哪条直线?写出正方形的顶点A,B,C,D的坐标.
图3-11
新课导入
因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).
(1)如图3-12,以点B为原点,分别以BC,AB所在直线为x轴,y轴,建立平面直角坐标系,规定1个单位长度为1,此时点B的坐标为(0,0).
图3-12
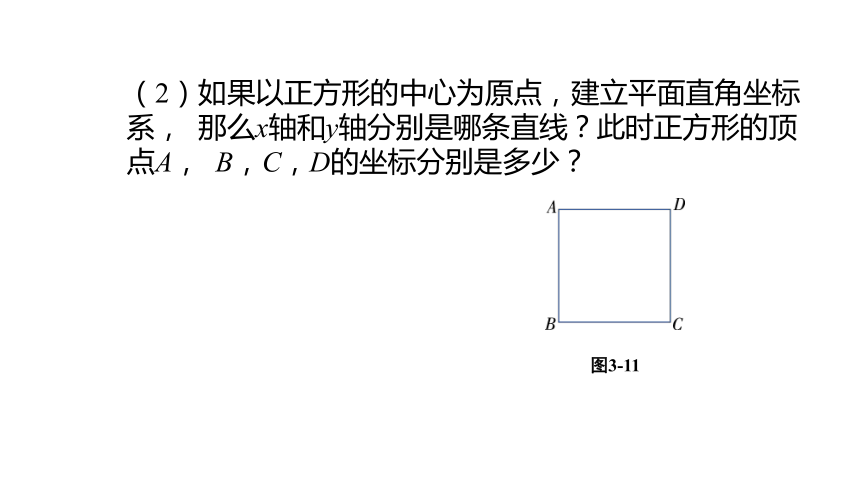
(2)如果以正方形的中心为原点,建立平面直角坐标系, 那么x轴和y轴分别是哪条直线?此时正方形的顶点A, B,C,D的坐标分别是多少?
图3-11
(2)如图3-13,以正方形的中心O为坐标原点,分别以过正方形的中心且垂直两组对边的两条对称轴为x轴,y轴,建立平面直角坐标系.
此时,点A,B,C,D的坐标分别为A(-3,3), B(-3,-3),C(3,-3),D(3,3).
平面直角坐标系的构建
不同,则点的坐标也不同.
在建立直角坐标系时,应使
点的坐标简明.
图3-13
例1 如图3-14,矩形ABCD的长和宽分别为8和6,
试建立适当的平面直角坐标系表示矩形ABCD
各顶点的坐标,并作出矩形ABCD.
图3-14
例题讲解
解 如图所示,以点B为坐标原点,分别以BC,AB 所在直线为x 轴,y轴,建立平面直角坐标系. 规定1个单位长度为1. 点B的坐标为(0,0).
因为BC = 8,AB = 6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6).
依次连接A,B,C,D , 则图3-15中的四边形就是所求作的矩形.
图3-15
●
A
C
●
D
●
在例1中,还可以怎样建立平面直角坐标系?
例2 图3-16 是一个机器零件的尺寸规格示意图,
试建立适当的平面直角坐标系表示其各顶点
的坐标,并作出这个示意图.
图3-16
规定1 个单位长度为100 mm,则四边形ABCD 的顶点
坐标分别为:A(-1,0),B(4,0),C(3,2),
D(0,2). 依次连接A,B,C,D , 则图3-17中的
四边形ABCD即为所求作的图形.
解 过点D 作AB 的垂线,垂足为点O,以点O 为原点, 分别以AB,DO所在直线为x轴,y轴,建立平面直角坐标系,如图3-17.
图3-17
画一画:你能在直角坐标系
里描出点A(-4,-5),B(-2,0),
C(4,0)吗?并连线.
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
探究
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
问题:你能求出△ABC的面积吗?
D
解:过点A作AD⊥x轴于点D.
∵A(-4,-5),∴D(-4,0) .
由点的坐标可得 AD=5 ,BC=6,
∴ S△ABC = ·BC·AD
= ×6×5=15.
例3在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说得到的是什么图形,并计算他们的面积.
3
2
1
-2
-1
-3
4
x
y
A
B
C
D
A
B
C
-1
-2
O
O
1
2
3
4
5
x
y
2
2
4
-2
-2
(2)A(-1,2),B(-2,-1),C(2,-1),D(3,2)
(1)A(5,1),B(2,1),
C(2,-3)
(1)得到一个直角三角形,
如图所示.
∴ S = ×3×4=6.
(2)得到一个平行四边形,
如图所示.
∴ S =3×4=12.
(6,8)
(0,4)
(4,0)
(-1,0)
(2,2)
随堂演练
5
[解析] S△ABC=3×4-×1×3-×2×4-×1×3=5.
解:答案不唯一,合理即可.(1)以正方形的中心为原点,一组对边中点所在的直线为x轴,另一组对边中点所在的直线为y轴建立平面直角坐标系,图略.则四个顶点的坐标分别为(-2,2),(-2,-2),(2,2),(2,-2);
(2)以两条邻边所在的直线分别为x轴和y轴,两邻边的交点为坐标原点建立平面直角坐标系,不在坐标轴上的顶点在第一象限,图略.则四个顶点的坐标分别为(0,0),(0,4),(4,0),(4,4).
坐标平面内的图形
坐标平面内图形面积的计算
建立适当的直角坐标系描述图形的位置
课堂小结
3.2 简单图形的坐标表示
问题 正方形ABCD的边长为4,请建立一个平面直角坐标系,并写出正方形的四个顶点A,B,C,D在这个平面直角坐标系中的坐标.
A
B
C
D
情景导入
(1)如果以点B为原点,以BC所在直线为x轴,建立平面直角坐标系,那么y轴是哪条直线?写出正方形的顶点A,B,C,D的坐标.
图3-11
新课导入
因为AB= 6,BC= 6,可得点A,C,D的坐标分别为A(0,6),C(6,0),D(6,6).
(1)如图3-12,以点B为原点,分别以BC,AB所在直线为x轴,y轴,建立平面直角坐标系,规定1个单位长度为1,此时点B的坐标为(0,0).
图3-12
(2)如果以正方形的中心为原点,建立平面直角坐标系, 那么x轴和y轴分别是哪条直线?此时正方形的顶点A, B,C,D的坐标分别是多少?
图3-11
(2)如图3-13,以正方形的中心O为坐标原点,分别以过正方形的中心且垂直两组对边的两条对称轴为x轴,y轴,建立平面直角坐标系.
此时,点A,B,C,D的坐标分别为A(-3,3), B(-3,-3),C(3,-3),D(3,3).
平面直角坐标系的构建
不同,则点的坐标也不同.
在建立直角坐标系时,应使
点的坐标简明.
图3-13
例1 如图3-14,矩形ABCD的长和宽分别为8和6,
试建立适当的平面直角坐标系表示矩形ABCD
各顶点的坐标,并作出矩形ABCD.
图3-14
例题讲解
解 如图所示,以点B为坐标原点,分别以BC,AB 所在直线为x 轴,y轴,建立平面直角坐标系. 规定1个单位长度为1. 点B的坐标为(0,0).
因为BC = 8,AB = 6,可得点A,C,D的坐标分别为:
A(0,6),C(8,0),D(8,6).
依次连接A,B,C,D , 则图3-15中的四边形就是所求作的矩形.
图3-15
●
A
C
●
D
●
在例1中,还可以怎样建立平面直角坐标系?
例2 图3-16 是一个机器零件的尺寸规格示意图,
试建立适当的平面直角坐标系表示其各顶点
的坐标,并作出这个示意图.
图3-16
规定1 个单位长度为100 mm,则四边形ABCD 的顶点
坐标分别为:A(-1,0),B(4,0),C(3,2),
D(0,2). 依次连接A,B,C,D , 则图3-17中的
四边形ABCD即为所求作的图形.
解 过点D 作AB 的垂线,垂足为点O,以点O 为原点, 分别以AB,DO所在直线为x轴,y轴,建立平面直角坐标系,如图3-17.
图3-17
画一画:你能在直角坐标系
里描出点A(-4,-5),B(-2,0),
C(4,0)吗?并连线.
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
探究
O
x
y
-5 -4 -3 -2 -1 1 2 3 4 5
4
3
2
1
-1
-2
-3
-4
-5
A
B
C
●
●
●
问题:你能求出△ABC的面积吗?
D
解:过点A作AD⊥x轴于点D.
∵A(-4,-5),∴D(-4,0) .
由点的坐标可得 AD=5 ,BC=6,
∴ S△ABC = ·BC·AD
= ×6×5=15.
例3在平面直角坐标系中描出下列各组点,并将各组内的点用线段依次连接起来得到一个封闭图形,说说得到的是什么图形,并计算他们的面积.
3
2
1
-2
-1
-3
4
x
y
A
B
C
D
A
B
C
-1
-2
O
O
1
2
3
4
5
x
y
2
2
4
-2
-2
(2)A(-1,2),B(-2,-1),C(2,-1),D(3,2)
(1)A(5,1),B(2,1),
C(2,-3)
(1)得到一个直角三角形,
如图所示.
∴ S = ×3×4=6.
(2)得到一个平行四边形,
如图所示.
∴ S =3×4=12.
(6,8)
(0,4)
(4,0)
(-1,0)
(2,2)
随堂演练
5
[解析] S△ABC=3×4-×1×3-×2×4-×1×3=5.
解:答案不唯一,合理即可.(1)以正方形的中心为原点,一组对边中点所在的直线为x轴,另一组对边中点所在的直线为y轴建立平面直角坐标系,图略.则四个顶点的坐标分别为(-2,2),(-2,-2),(2,2),(2,-2);
(2)以两条邻边所在的直线分别为x轴和y轴,两邻边的交点为坐标原点建立平面直角坐标系,不在坐标轴上的顶点在第一象限,图略.则四个顶点的坐标分别为(0,0),(0,4),(4,0),(4,4).
坐标平面内的图形
坐标平面内图形面积的计算
建立适当的直角坐标系描述图形的位置
课堂小结
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
