九年级数学下册-第三十二章 投影与视图 复习课件-冀教版(共26张ppt)
文档属性
| 名称 | 九年级数学下册-第三十二章 投影与视图 复习课件-冀教版(共26张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览








文档简介
(共26张PPT)
第三十二章
投影与视图
复习课件
知识结构图:
中心投影
投影与视图
视图
投影
平行投影
基本几何体的三视图
基本几何体的平面展开图
(1)投影:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,其中照射光线叫做投影线,投影所在的平面叫做投影面。
考点聚焦
考点1
投影
(2)平行投影:由平行光线(如太阳光线)所形成的投影,称为平行投影。其中正投影是指投影线垂直投影面产生的平行投影。
太阳光
(3)中心投影:手电筒、路灯和台灯的光线可以看成是从一点出发的,像这样的光线所形成的投影称为中心投影。
1、晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是【
】
A.变长
B.变短
C.先变长后变短
D.先变短后变长
D
2、小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为【
】
A.上午12时
B.上午10时
C.上午9时30分
D.上午8时
D
做一做
3、已知两棵小树在同一时刻的影子,你如何确定影子是在太阳光线下还是在灯光的光线下形成的。
做一做
两光线相交于一点,因此它们是灯光下形成的。
两条光线是平行,因此它们是太阳光下形成的。
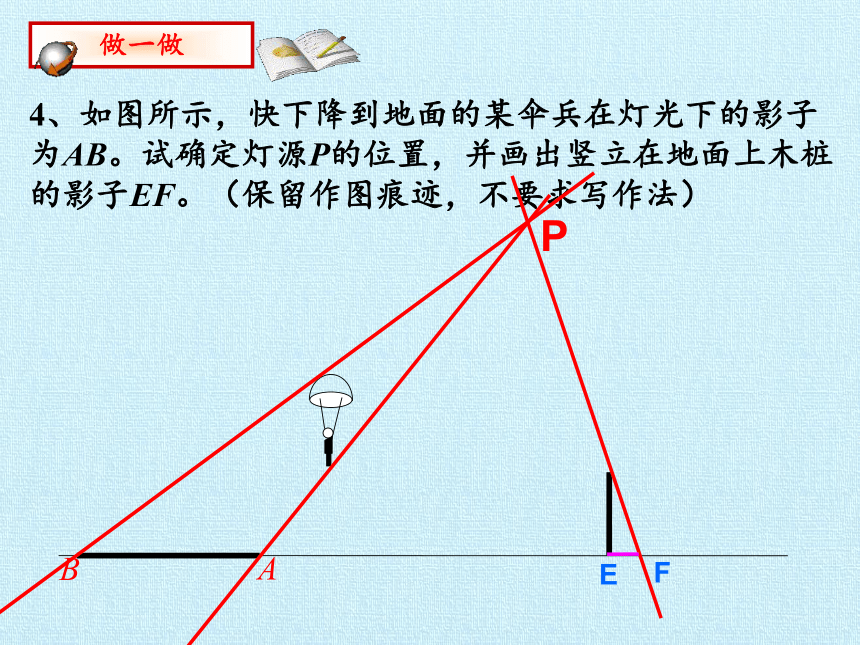
4、如图所示,快下降到地面的某伞兵在灯光下的影子为AB。试确定灯源P的位置,并画出竖立在地面上木桩的影子EF。(保留作图痕迹,不要求写作法)
做一做
A
B
P
E
F
考点2 物体的三视图
1.三视图
①主视图
从正面看到的图
②左视图
从左面看到的图
③俯视图
从上面看到的图
主视图
从正面看到的图
左视图
从左面看到的图
俯视图
从上面看到的图
2.画“三视图”的原则
左视图
俯视图
①位置:
主视图
左视图
俯视图
②大小:
长对正,高平齐,
宽相等。
③虚实:
在画图时,看得见
部分的轮廓线通常
画成实线,看不见
部分的轮廓线通常
画成虚线。
长对正
宽相等
长
高
宽
主视图
高平齐
1.如图,一桶未启封的方便面摆放在桌面上,则它的俯视图是(
)
2.将如图所示的Rt△ABC绕直角边AC旋转一周,所得几何体的主视图是(
)
C
A
B
C
A.
B.
C.
D.
D
做一做
3.右图是由相同小正方形搭的几何体的俯视图(小正方形中所标的数字表示在该位置上小正方体的个数),则这个几何体的左视图是(
)
1
3
2
2
1
1
C
4.如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m。若小芳比爸爸矮0.3m,则她的影长为( )
A.1.3m
B.1.65m
C.1.75m
D.1.8m
C
A.
B.
C.
D.
5.如图所示支架(一种小零件,支架的两个台阶的高度和宽度都是同一长度)的主视图是(
)
正面
A.
B.
C.
D.
C
6.由几个大小相同的小正方体组成的立体图形的俯视图如图所示,则这个立体图形应是下图中的( )
俯视图
A.
B.
C.
D.
C
7.如下图,是由一些相同的小正方体构成的几何体的三视图,请问这几何体小正方体中的个数是
。
A.
9
B.
10
C.
11
D.
12
A
左视图
主视图
俯视图
A
B
C
D
8.有一实物如图,那么它的主视图(
)
B
9.如图所示是某种型号的正六角螺母毛坯的三视图,则它的表面积为
。
主视图
2cm
3cm
左视图
俯视图
考点3 基本几何体的平面展开图
1.沿柱体、椎体的母线展开,观察可得到侧面展开图。
2.圆柱柱和圆锥的侧面展开图分别是矩形和扇形。
如图所示,已知一个长方体纸箱的长、宽和高分别为30cm,20cm,10cm。一只昆虫从纸箱的顶点A处沿纸箱表面ACDE和表面GEDB爬到另一个顶点B处。它沿哪条路线爬行的距离最短?请说明理由,并求出这个最短距离。(结果保留两位小数)
共同探究
思考:
1.长方体有几种展开方式,使得点A与点B在同一个平面上?
2.在同一平面上如何求两点之间的最短距离?
3.长方体的展开图中,哪个展开图中A,B两点之间的距离最短?
解:如图所示,将这个长方体纸箱的表面展开,连接AB。根据“两点之间线段最短”,可知线段AB就是昆虫爬行距离最短的路线。
在Rt△ABC中,AC=30cm,BC=BD+CD=20+10=30(cm)。
根据勾股定理,得:
≈42.43(cm),
即昆虫最短爬行路线的距离约为42.43cm。
2.常见图形的侧面展开图:圆锥的侧面展开图是一个扇形,其中扇形的半径是圆锥的母线长,扇形的弧长是底面圆的周长;圆柱的侧面展开图是矩形,矩形的一边长是圆柱的底面周长,另一边长是圆柱的高;正方体的表面展开图有11种情况;棱柱的侧面展开图是矩形,矩形的一边长是棱柱的底面周长,另一边长是棱柱的侧棱长。
[知识拓展]
1.立体图形是由面围成的,同一个立体图形,沿不同方式展开,得到的平面图形是不同的。
检测反馈
1.下面的图形中,是三棱柱的侧面展开图的是( )
解析:棱柱的侧面展开图是矩形,三棱柱的侧面展开图是3个矩形。故选A。
A
2.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
解析:A中展开图“预”的对面是“考”,不符合要求,故A错误;B中“预”的对面是“功”,不符合要求,故B错误;C中“预”的对面是“中”,“成”的对面是“功”,符合题意,故C正确;D中“预”的对面是“中”,“成”的对面是“祝”,不符合题意,故D错误。故选C。
C
3.如果圆锥的母线长为5cm,底面半径为3cm,那么圆锥的全面积为 。
解析:圆锥的侧面积为
×5×(3×2×π)=15π(cm2),底面积为π×32=9π(cm2),所以圆锥的全面积为15π+9π=24π(cm2)。故填24πcm2。
24πcm2
4.如图所示的是一个食品包装盒的平面展开图。
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面积之和)。
解:(1)这个多面体是正六棱柱。
(2)S侧=6ab,S底=6×
b2=
b2,
所以S全面积=S侧+2S底=6ab+3
b2。
谢
谢
第三十二章
投影与视图
复习课件
知识结构图:
中心投影
投影与视图
视图
投影
平行投影
基本几何体的三视图
基本几何体的平面展开图
(1)投影:一般地,用光线照射物体,在某个平面(地面、墙壁等)上得到的影子叫做物体的投影,其中照射光线叫做投影线,投影所在的平面叫做投影面。
考点聚焦
考点1
投影
(2)平行投影:由平行光线(如太阳光线)所形成的投影,称为平行投影。其中正投影是指投影线垂直投影面产生的平行投影。
太阳光
(3)中心投影:手电筒、路灯和台灯的光线可以看成是从一点出发的,像这样的光线所形成的投影称为中心投影。
1、晚上,小华出去散步,在经过一盏路灯时,他发现自己的身影是【
】
A.变长
B.变短
C.先变长后变短
D.先变短后变长
D
2、小亮在上午8时、9时30分、10时、12时四次到室外的阳光下观察向日葵的头茎随太阳转动的情况,无意之中,他发现这四个时刻向日葵影子的长度各不相同,那么影子最长的时刻为【
】
A.上午12时
B.上午10时
C.上午9时30分
D.上午8时
D
做一做
3、已知两棵小树在同一时刻的影子,你如何确定影子是在太阳光线下还是在灯光的光线下形成的。
做一做
两光线相交于一点,因此它们是灯光下形成的。
两条光线是平行,因此它们是太阳光下形成的。
4、如图所示,快下降到地面的某伞兵在灯光下的影子为AB。试确定灯源P的位置,并画出竖立在地面上木桩的影子EF。(保留作图痕迹,不要求写作法)
做一做
A
B
P
E
F
考点2 物体的三视图
1.三视图
①主视图
从正面看到的图
②左视图
从左面看到的图
③俯视图
从上面看到的图
主视图
从正面看到的图
左视图
从左面看到的图
俯视图
从上面看到的图
2.画“三视图”的原则
左视图
俯视图
①位置:
主视图
左视图
俯视图
②大小:
长对正,高平齐,
宽相等。
③虚实:
在画图时,看得见
部分的轮廓线通常
画成实线,看不见
部分的轮廓线通常
画成虚线。
长对正
宽相等
长
高
宽
主视图
高平齐
1.如图,一桶未启封的方便面摆放在桌面上,则它的俯视图是(
)
2.将如图所示的Rt△ABC绕直角边AC旋转一周,所得几何体的主视图是(
)
C
A
B
C
A.
B.
C.
D.
D
做一做
3.右图是由相同小正方形搭的几何体的俯视图(小正方形中所标的数字表示在该位置上小正方体的个数),则这个几何体的左视图是(
)
1
3
2
2
1
1
C
4.如图,小芳和爸爸正在散步,爸爸身高1.8m,他在地面上的影长为2.1m。若小芳比爸爸矮0.3m,则她的影长为( )
A.1.3m
B.1.65m
C.1.75m
D.1.8m
C
A.
B.
C.
D.
5.如图所示支架(一种小零件,支架的两个台阶的高度和宽度都是同一长度)的主视图是(
)
正面
A.
B.
C.
D.
C
6.由几个大小相同的小正方体组成的立体图形的俯视图如图所示,则这个立体图形应是下图中的( )
俯视图
A.
B.
C.
D.
C
7.如下图,是由一些相同的小正方体构成的几何体的三视图,请问这几何体小正方体中的个数是
。
A.
9
B.
10
C.
11
D.
12
A
左视图
主视图
俯视图
A
B
C
D
8.有一实物如图,那么它的主视图(
)
B
9.如图所示是某种型号的正六角螺母毛坯的三视图,则它的表面积为
。
主视图
2cm
3cm
左视图
俯视图
考点3 基本几何体的平面展开图
1.沿柱体、椎体的母线展开,观察可得到侧面展开图。
2.圆柱柱和圆锥的侧面展开图分别是矩形和扇形。
如图所示,已知一个长方体纸箱的长、宽和高分别为30cm,20cm,10cm。一只昆虫从纸箱的顶点A处沿纸箱表面ACDE和表面GEDB爬到另一个顶点B处。它沿哪条路线爬行的距离最短?请说明理由,并求出这个最短距离。(结果保留两位小数)
共同探究
思考:
1.长方体有几种展开方式,使得点A与点B在同一个平面上?
2.在同一平面上如何求两点之间的最短距离?
3.长方体的展开图中,哪个展开图中A,B两点之间的距离最短?
解:如图所示,将这个长方体纸箱的表面展开,连接AB。根据“两点之间线段最短”,可知线段AB就是昆虫爬行距离最短的路线。
在Rt△ABC中,AC=30cm,BC=BD+CD=20+10=30(cm)。
根据勾股定理,得:
≈42.43(cm),
即昆虫最短爬行路线的距离约为42.43cm。
2.常见图形的侧面展开图:圆锥的侧面展开图是一个扇形,其中扇形的半径是圆锥的母线长,扇形的弧长是底面圆的周长;圆柱的侧面展开图是矩形,矩形的一边长是圆柱的底面周长,另一边长是圆柱的高;正方体的表面展开图有11种情况;棱柱的侧面展开图是矩形,矩形的一边长是棱柱的底面周长,另一边长是棱柱的侧棱长。
[知识拓展]
1.立体图形是由面围成的,同一个立体图形,沿不同方式展开,得到的平面图形是不同的。
检测反馈
1.下面的图形中,是三棱柱的侧面展开图的是( )
解析:棱柱的侧面展开图是矩形,三棱柱的侧面展开图是3个矩形。故选A。
A
2.小亮为今年参加中考的好友小杰制作了一个正方体礼品盒(如图所示),六个面上各有一个字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
解析:A中展开图“预”的对面是“考”,不符合要求,故A错误;B中“预”的对面是“功”,不符合要求,故B错误;C中“预”的对面是“中”,“成”的对面是“功”,符合题意,故C正确;D中“预”的对面是“中”,“成”的对面是“祝”,不符合题意,故D错误。故选C。
C
3.如果圆锥的母线长为5cm,底面半径为3cm,那么圆锥的全面积为 。
解析:圆锥的侧面积为
×5×(3×2×π)=15π(cm2),底面积为π×32=9π(cm2),所以圆锥的全面积为15π+9π=24π(cm2)。故填24πcm2。
24πcm2
4.如图所示的是一个食品包装盒的平面展开图。
(1)请写出这个包装盒的多面体形状的名称;
(2)请根据图中所标的尺寸,计算这个多面体的侧面积和全面积(侧面积与两个底面积之和)。
解:(1)这个多面体是正六棱柱。
(2)S侧=6ab,S底=6×
b2=
b2,
所以S全面积=S侧+2S底=6ab+3
b2。
谢
谢
