八年级数学上册-第三章 位置与坐标 复习课件-北师大版(共22张ppt)
文档属性
| 名称 | 八年级数学上册-第三章 位置与坐标 复习课件-北师大版(共22张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 282.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:23:55 | ||
图片预览





文档简介
(共22张PPT)
第三章
位置与坐标
复习课件
复习目标:
1.在给定的坐标系中,会根据坐标描出点的位置,能由点的位置写出它的坐标并会在直角坐标系中作出简单图形;
2.在同一坐标系中,感受图形变换后点的坐标的变化;
3.综合运用图形与坐标的知识解决简单的实际问题,初步建立数形结合的数学思想。
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
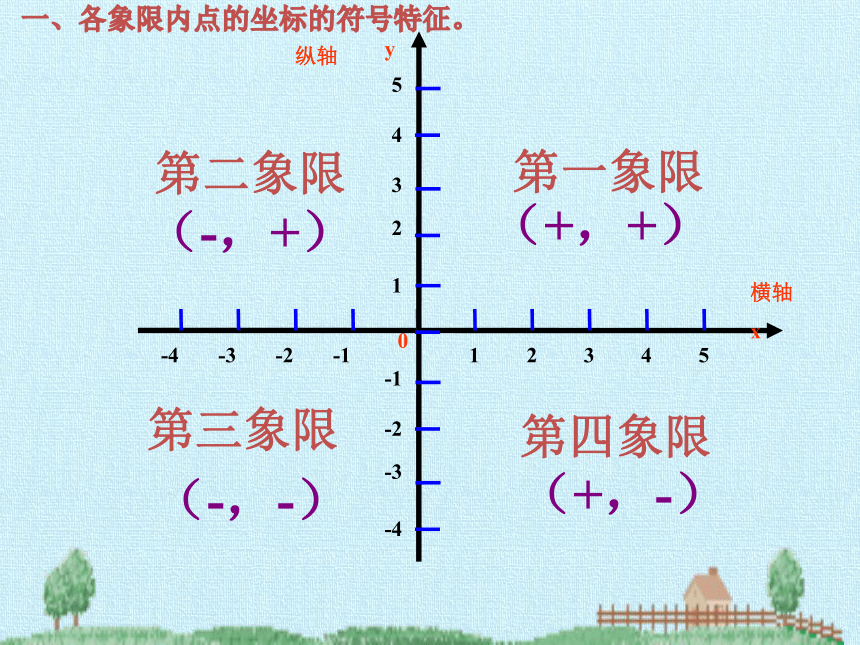
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
横轴
x
一、各象限内点的坐标的符号特征。
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
知识应用
1.点P的坐标是(2,-3),则点P在第 象限。
2.若点P(x,y)的坐标满足xy>0,则点P在第__________象限;
3.若点P(x,y)的坐标满足xy<0,且在x轴上方,则点P在第
象限。
四
一或三
二
X
Y
1
2
3
4
3
1
4
2
5
5
0
·
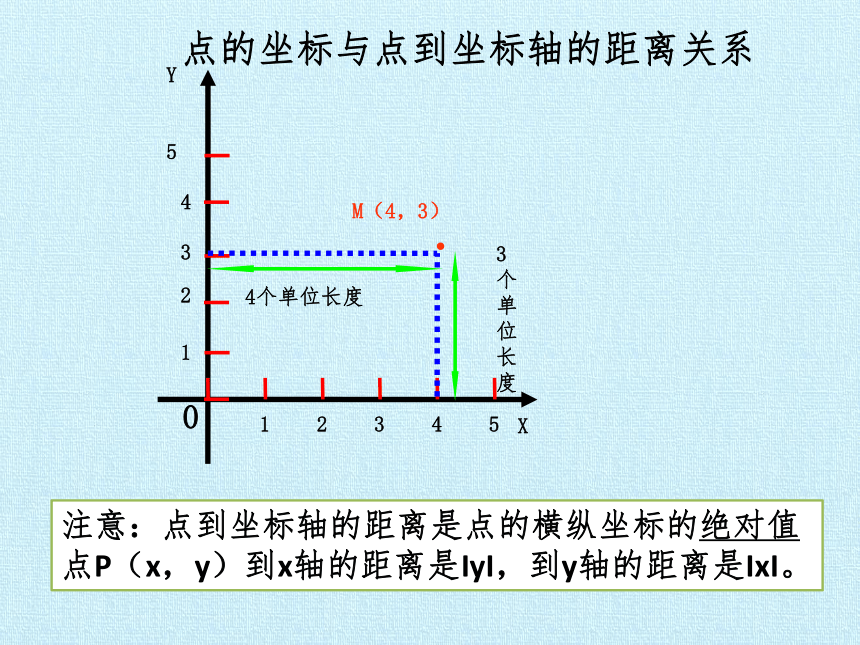
M(4,3)
4个单位长度
3个单位长度
点的坐标与点到坐标轴的距离关系
注意:点到坐标轴的距离是点的横纵坐标的绝对值点P(x,y)到x轴的距离是IyI,到y轴的距离是IxI。
4.若点A的坐标是(-3,5),则它到x轴的距离是_____,_____到y轴的距离是_________。
5.若点B在X轴上方,Y轴右侧,并且到y轴、x轴距离分别是2、4个单位长度,则点B的坐标是____________________________________________。
5
3
(2,4)
(1,2)、(1,-2)、(-1,2)、(-1,-2)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
A
B
C
D
x
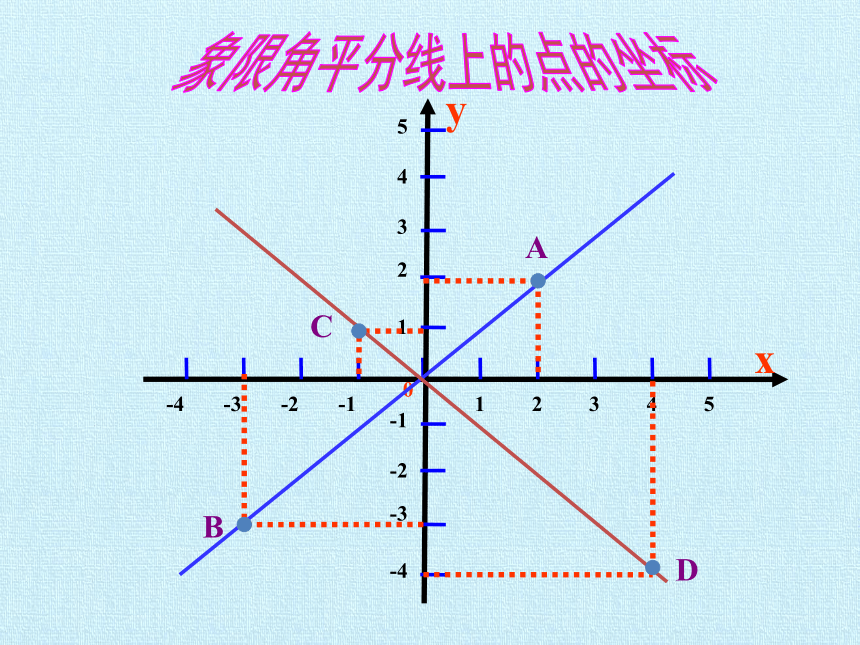
象限角平分线上的点的坐标
0
1
-1
1
-1
x
y
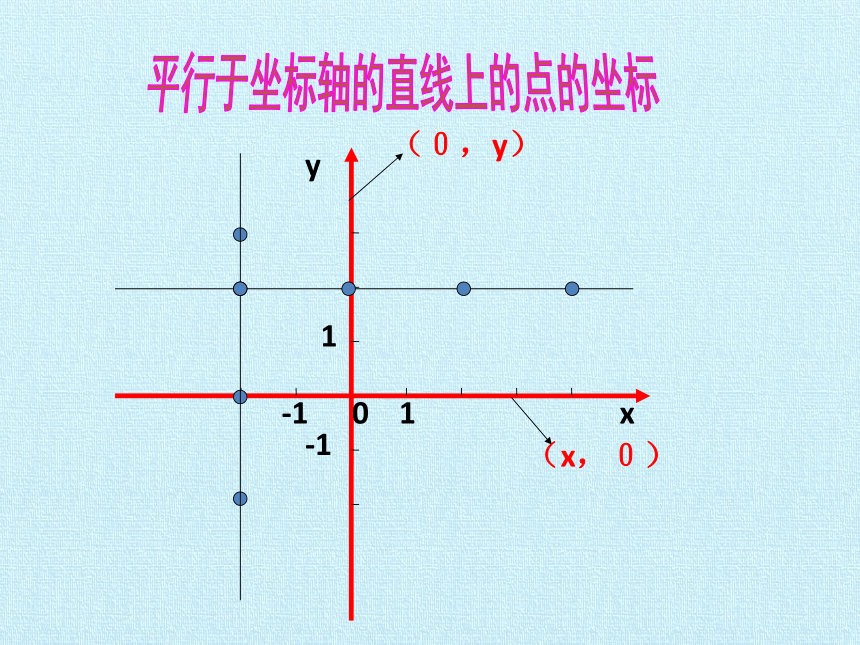
(x,0)
(0,y)
平行于坐标轴的直线上的点的坐标
1.一、三象限的角平分线上的点的横纵坐标相等,二、四象限的角平分线上的点的横纵坐标互为相反数。
平行于y轴的直线上的各点的横坐标相同,纵坐标不同。
2.平行于x轴的直线上的各点的纵坐标相同,横坐标不同。
知识要点二
1.已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是______________。
2.已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为
。
(2,2)或者(-2,2)
-1
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
对称点的坐标
知识要点三
1.关于X轴对称的两个点横坐标相等,纵坐标互为相反数。
2.关于Y轴对称的两个点纵坐标相等,横坐标互为相反数。
3.点A(-1,-3)关于x轴对称点的坐标是
_________。关于y轴对称的点坐标是
________。
(-1,3)
(1,-3)
1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;若点(a+1,-5)在y轴上,则a=______。
4.若点P在第三象限且到x轴的距离2,到y轴的距离为1.5,则点P的坐标是_____________。
3.点M(-8,12)到x轴的距离是_____,到y轴的距离是_____。
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是____________________。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
快速练一练
6.如果同一直角坐标系两个点的横坐标相同,那么过这两点的直线(
)
A、平行于x轴
B、平行于y轴
C、经过原点
D、以上都不对
7.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
5.在平面直角坐标系内,已知点P
(a,b),
且ab<0,则点P的位置在____________。
第二或四象限
B
a<0
b>1
8.点A(1-a,5),B(3,b)关于y轴对称,则a=___,b=____。
5
4
快速练一练
10.点(4,3)与点(4,-3)的关系是【
】。
(A)关于原点对称
(B)关于x轴对称
(C)关于y轴对称
(D)不能构成对称关系
9.实数x,y满足(x-1)2+
|y|
=
0,则点
P(x,y)在【
】。
(A)原点
(B)x轴正半轴
(C)第一象限
(D)任意位置
B
B
快速练一练
11.如图所示,在平面直角坐标系中,菱形MNPO的顶点P坐标是(3,4),则顶点M、N的坐标分别是
。
M(5,0),N(8,4)
(3,4)
E
F
能力提升
O
C
B
A
1、已知等边△ABC的两个顶点坐标为A(-4,0),B(2,0),求:
(1)点C的坐标;
(2)△ABC的面积。
2、如图所示,在直角梯形OABC中,CB∥OA,CB=8,OC=8,∠OAB=45°。
(1)求点A、B、C的坐标;
(2)求△ABC的面积。
拓展延伸
已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标。
(m,-m)
(m,m)
x<0
y<0
x<0
y>0
x>0
y<0
x>0
y>0
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
二四象限
一三象限
第四象限
第三象限
第二象限
第一象限
平行于y轴
平行于x轴
原点
y轴
x轴
象限角平分线上的点
点P(x,y)在各象限的坐标特点
连线平行于坐标轴的点
坐标轴上点P(x,y)
特殊位置点的特殊坐标:
谢
谢
第三章
位置与坐标
复习课件
复习目标:
1.在给定的坐标系中,会根据坐标描出点的位置,能由点的位置写出它的坐标并会在直角坐标系中作出简单图形;
2.在同一坐标系中,感受图形变换后点的坐标的变化;
3.综合运用图形与坐标的知识解决简单的实际问题,初步建立数形结合的数学思想。
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
纵轴
第一象限
第二象限
第三象限
第四象限
(+,+)
(-,+)
(-,-)
(+,-)
横轴
x
一、各象限内点的坐标的符号特征。
下列各点分别在坐标平面的什么位置上?
A(3,2)
B(0,-2)
C(-3,-2)
D(-3,0)
E(-1.5,3.5)
F(2,-3)
第一象限
第三象限
第二象限
第四象限
y轴上
x轴上
知识应用
1.点P的坐标是(2,-3),则点P在第 象限。
2.若点P(x,y)的坐标满足xy>0,则点P在第__________象限;
3.若点P(x,y)的坐标满足xy<0,且在x轴上方,则点P在第
象限。
四
一或三
二
X
Y
1
2
3
4
3
1
4
2
5
5
0
·
M(4,3)
4个单位长度
3个单位长度
点的坐标与点到坐标轴的距离关系
注意:点到坐标轴的距离是点的横纵坐标的绝对值点P(x,y)到x轴的距离是IyI,到y轴的距离是IxI。
4.若点A的坐标是(-3,5),则它到x轴的距离是_____,_____到y轴的距离是_________。
5.若点B在X轴上方,Y轴右侧,并且到y轴、x轴距离分别是2、4个单位长度,则点B的坐标是____________________________________________。
5
3
(2,4)
(1,2)、(1,-2)、(-1,2)、(-1,-2)
0
1
2
3
4
5
-4
-3
-2
-1
3
1
4
2
5
-2
-4
-1
-3
y
A
B
C
D
x
象限角平分线上的点的坐标
0
1
-1
1
-1
x
y
(x,0)
(0,y)
平行于坐标轴的直线上的点的坐标
1.一、三象限的角平分线上的点的横纵坐标相等,二、四象限的角平分线上的点的横纵坐标互为相反数。
平行于y轴的直线上的各点的横坐标相同,纵坐标不同。
2.平行于x轴的直线上的各点的纵坐标相同,横坐标不同。
知识要点二
1.已知:A(1,2),B(x,y),AB∥x轴,且B到y轴距离为2,则点B的坐标是______________。
2.已知点A(m,-2),点B(3,m-1),且直线AB∥x轴,则m的值为
。
(2,2)或者(-2,2)
-1
0
1
-1
1
-1
x
y
P(a,b)
A(a,-b)
B(-a,b)
对称点的坐标
知识要点三
1.关于X轴对称的两个点横坐标相等,纵坐标互为相反数。
2.关于Y轴对称的两个点纵坐标相等,横坐标互为相反数。
3.点A(-1,-3)关于x轴对称点的坐标是
_________。关于y轴对称的点坐标是
________。
(-1,3)
(1,-3)
1.点(3,-2)在第_____象限;点(-1.5,-1)在第_______象限;点(0,3)在____轴上;若点(a+1,-5)在y轴上,则a=______。
4.若点P在第三象限且到x轴的距离2,到y轴的距离为1.5,则点P的坐标是_____________。
3.点M(-8,12)到x轴的距离是_____,到y轴的距离是_____。
2.点A在x轴上,距离原点4个单位长度,则A点的坐标是____________________。
四
三
y
-1
(4,0)或(-4,0)
12
8
(-1.5,-2)
快速练一练
6.如果同一直角坐标系两个点的横坐标相同,那么过这两点的直线(
)
A、平行于x轴
B、平行于y轴
C、经过原点
D、以上都不对
7.若点(a,b-1)在第二象限,则a的取值范围是_____,b的取值范围________。
5.在平面直角坐标系内,已知点P
(a,b),
且ab<0,则点P的位置在____________。
第二或四象限
B
a<0
b>1
8.点A(1-a,5),B(3,b)关于y轴对称,则a=___,b=____。
5
4
快速练一练
10.点(4,3)与点(4,-3)的关系是【
】。
(A)关于原点对称
(B)关于x轴对称
(C)关于y轴对称
(D)不能构成对称关系
9.实数x,y满足(x-1)2+
|y|
=
0,则点
P(x,y)在【
】。
(A)原点
(B)x轴正半轴
(C)第一象限
(D)任意位置
B
B
快速练一练
11.如图所示,在平面直角坐标系中,菱形MNPO的顶点P坐标是(3,4),则顶点M、N的坐标分别是
。
M(5,0),N(8,4)
(3,4)
E
F
能力提升
O
C
B
A
1、已知等边△ABC的两个顶点坐标为A(-4,0),B(2,0),求:
(1)点C的坐标;
(2)△ABC的面积。
2、如图所示,在直角梯形OABC中,CB∥OA,CB=8,OC=8,∠OAB=45°。
(1)求点A、B、C的坐标;
(2)求△ABC的面积。
拓展延伸
已知两点D(1,-3)、E(-1,-4),试在直线l上确定一点Q,使点Q到D、E两点的距离之和最小,并求出Q点坐标。
(m,-m)
(m,m)
x<0
y<0
x<0
y>0
x>0
y<0
x>0
y>0
横坐标相同
纵坐标相同
(0,0)
(0,y)
(x,0)
二四象限
一三象限
第四象限
第三象限
第二象限
第一象限
平行于y轴
平行于x轴
原点
y轴
x轴
象限角平分线上的点
点P(x,y)在各象限的坐标特点
连线平行于坐标轴的点
坐标轴上点P(x,y)
特殊位置点的特殊坐标:
谢
谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
