沪教版(上海)初中数学七年级第一学期 9.12 乘法公式复习讲义(乘法公式的再认识) 教案
文档属性
| 名称 | 沪教版(上海)初中数学七年级第一学期 9.12 乘法公式复习讲义(乘法公式的再认识) 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 270.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:30:46 | ||
图片预览

文档简介
乘法公式复习讲义
(乘法公式的再认识)
一、教学目标
知识与技能:通过乘法公式复习,进一步提高观察力、发展符号感;从广泛意义上理解公式中的字母含义;熟练运用乘法公式;掌握乘法公式几何背景
过程与方法:利用长方形的面积变化,推导出乘法公式。
情感态度与价值观:体会数形结合的数学思想.在合作、交流和讨论中体会数学学习的乐趣.
二、教学重点及难点
教学重点:熟练运用乘法公式;
教学难点:乘法公式几何背景
教学过程
一.复习
1.平方差公式:两个数的和与这两个数的差的乘积等于这两个数的平方差,
既:
2.完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们积的两倍
用符号来表示
(错题纠正)1.判断下列运算是否正确并说明理由
(校正练习)2.计算下列各式
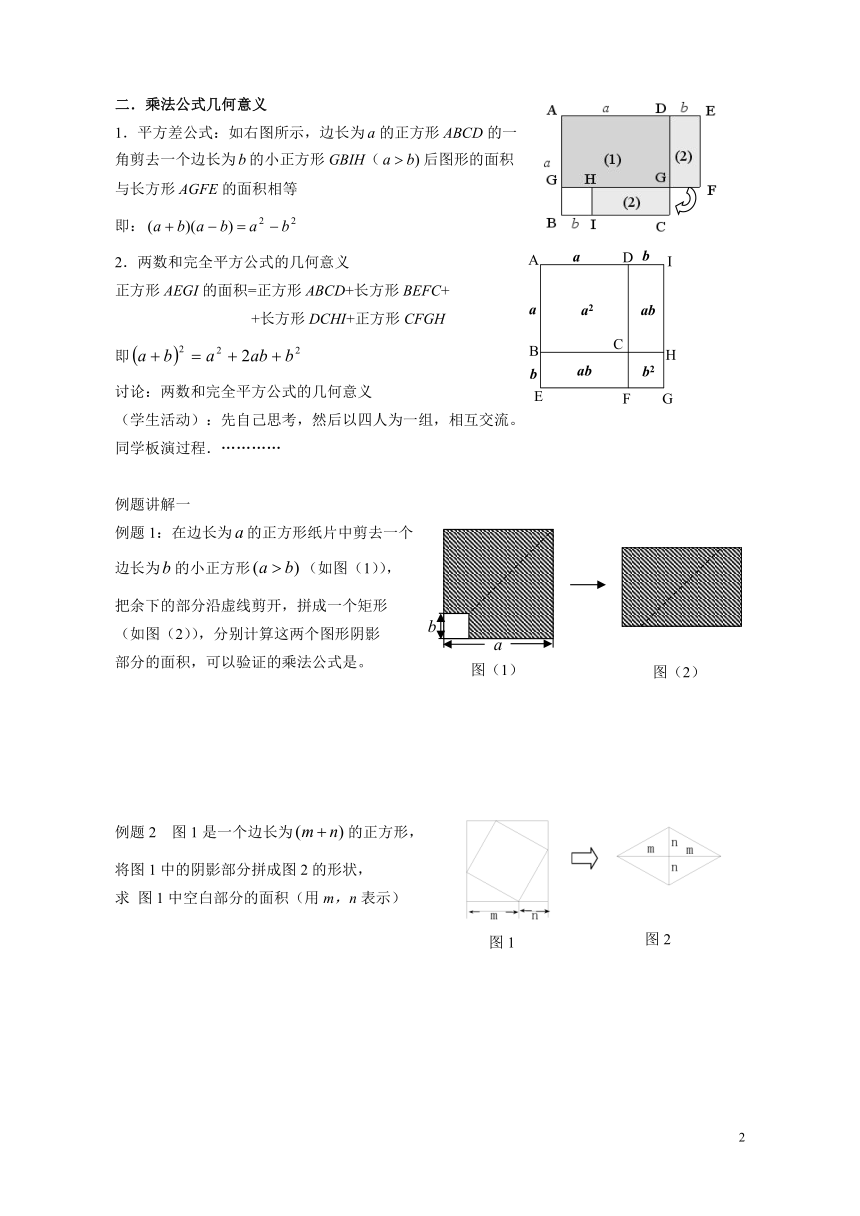
二.乘法公式几何意义
1.平方差公式:如右图所示,边长为的正方形ABCD的一
角剪去一个边长为的小正方形GBIH(后图形的面积
与长方形AGFE的面积相等
即:
2.两数和完全平方公式的几何意义
正方形AEGI的面积=正方形ABCD+长方形BEFC+
+长方形DCHI+正方形CFGH
即
讨论:两数和完全平方公式的几何意义
(学生活动):先自己思考,然后以四人为一组,相互交流。
同学板演过程.…………
例题讲解一
例题1:在边长为的正方形纸片中剪去一个
边长为的小正方形(如图(1)),
把余下的部分沿虚线剪开,拼成一个矩形
(如图(2)),分别计算这两个图形阴影
部分的面积,可以验证的乘法公式是。
例题2
图1是一个边长为的正方形,
将图1中的阴影部分拼成图2的形状,
求
图1中空白部分的面积(用m,n表示)
巩固练习一
练习1、从边长为的大正方形纸板中挖去
一个边长为的小正方形纸板后,将其裁
成四个相同的等腰梯形(如图1),然后
拼成一个平行四边形(如图2).那么通
过计算两个图形阴影部分的面积,可以
验证成立的公式为
:
练习2.图1是一个长为2
m,宽为2
n的长方形,
沿图中虚线用剪刀均分成四块小长方形,
然后按图2的形状拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1:
方法2:
(3)观察图2你能写出下列三个
代数式之间的等量关系吗?
代数式:
(4)根据(3)题中的等量关系,解决如下问题:
①若求
②若,求的值
③若,求的值
④若,,求的值
练习3.已知:,求的值.
练习4.已知(若一个数与它的倒数的和等于4,那么这个数与它的倒数的差的平方是多少),求的值
例题3已知
,求的值
例题4
若,判断、、的数量关系
课后练习
1.阅读下面的材料并解答问题:我们知道,完全平方公式可以用几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如就可以用图①或图②等图形的面积表示:
(1)请写出图③所表示的代数恒等式:____________________;
(2)试画出一个几何图形,使它的面积能表示为:;
(3)请仿照上述方法另写一个含、的代数恒等式,并画出与之对应的几何图形。
2.有若干张如图所示的正方形和长方形(数量足够多),
请你利用这些卡片拼成一些正方形和长方形(卡片可以
重叠),利用所拼成的图形的面积的不同表示方法写出一
些等式(在所拼的图形中,至少有两个图形包括三种不同
形状的卡片,画出示意图并写出相应的等示)。
3.已知,,,
求代数式的值
4.若、满足,求的值
5.已知:△ABC的三边长分别为a、b、c,且a、b、c满足等式,试说明该三角形是三条边的数量关系.
图(1)
图(2)
图1
图2
图1
图2
n
n
n
n
m
m
m
m
图2
m
m
n
n
图1
PAGE
1
(乘法公式的再认识)
一、教学目标
知识与技能:通过乘法公式复习,进一步提高观察力、发展符号感;从广泛意义上理解公式中的字母含义;熟练运用乘法公式;掌握乘法公式几何背景
过程与方法:利用长方形的面积变化,推导出乘法公式。
情感态度与价值观:体会数形结合的数学思想.在合作、交流和讨论中体会数学学习的乐趣.
二、教学重点及难点
教学重点:熟练运用乘法公式;
教学难点:乘法公式几何背景
教学过程
一.复习
1.平方差公式:两个数的和与这两个数的差的乘积等于这两个数的平方差,
既:
2.完全平方公式:两数和(或差)的平方,等于它们的平方和,加上(或减去)它们积的两倍
用符号来表示
(错题纠正)1.判断下列运算是否正确并说明理由
(校正练习)2.计算下列各式
二.乘法公式几何意义
1.平方差公式:如右图所示,边长为的正方形ABCD的一
角剪去一个边长为的小正方形GBIH(后图形的面积
与长方形AGFE的面积相等
即:
2.两数和完全平方公式的几何意义
正方形AEGI的面积=正方形ABCD+长方形BEFC+
+长方形DCHI+正方形CFGH
即
讨论:两数和完全平方公式的几何意义
(学生活动):先自己思考,然后以四人为一组,相互交流。
同学板演过程.…………
例题讲解一
例题1:在边长为的正方形纸片中剪去一个
边长为的小正方形(如图(1)),
把余下的部分沿虚线剪开,拼成一个矩形
(如图(2)),分别计算这两个图形阴影
部分的面积,可以验证的乘法公式是。
例题2
图1是一个边长为的正方形,
将图1中的阴影部分拼成图2的形状,
求
图1中空白部分的面积(用m,n表示)
巩固练习一
练习1、从边长为的大正方形纸板中挖去
一个边长为的小正方形纸板后,将其裁
成四个相同的等腰梯形(如图1),然后
拼成一个平行四边形(如图2).那么通
过计算两个图形阴影部分的面积,可以
验证成立的公式为
:
练习2.图1是一个长为2
m,宽为2
n的长方形,
沿图中虚线用剪刀均分成四块小长方形,
然后按图2的形状拼成一个正方形.
(1)你认为图2中的阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图b中阴影部分的面积.
方法1:
方法2:
(3)观察图2你能写出下列三个
代数式之间的等量关系吗?
代数式:
(4)根据(3)题中的等量关系,解决如下问题:
①若求
②若,求的值
③若,求的值
④若,,求的值
练习3.已知:,求的值.
练习4.已知(若一个数与它的倒数的和等于4,那么这个数与它的倒数的差的平方是多少),求的值
例题3已知
,求的值
例题4
若,判断、、的数量关系
课后练习
1.阅读下面的材料并解答问题:我们知道,完全平方公式可以用几何图形的面积来表示,实际上还有一些代数恒等式也可以用这种形式表示,例如就可以用图①或图②等图形的面积表示:
(1)请写出图③所表示的代数恒等式:____________________;
(2)试画出一个几何图形,使它的面积能表示为:;
(3)请仿照上述方法另写一个含、的代数恒等式,并画出与之对应的几何图形。
2.有若干张如图所示的正方形和长方形(数量足够多),
请你利用这些卡片拼成一些正方形和长方形(卡片可以
重叠),利用所拼成的图形的面积的不同表示方法写出一
些等式(在所拼的图形中,至少有两个图形包括三种不同
形状的卡片,画出示意图并写出相应的等示)。
3.已知,,,
求代数式的值
4.若、满足,求的值
5.已知:△ABC的三边长分别为a、b、c,且a、b、c满足等式,试说明该三角形是三条边的数量关系.
图(1)
图(2)
图1
图2
图1
图2
n
n
n
n
m
m
m
m
图2
m
m
n
n
图1
PAGE
1
