沪教版(上海)初中数学八年级第一学期 18.3 反比例函数的图像与性质 教案
文档属性
| 名称 | 沪教版(上海)初中数学八年级第一学期 18.3 反比例函数的图像与性质 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 185.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 21:02:00 | ||
图片预览


文档简介
18.3(2)反比例函数的图像与性质
教学目标
1、巩固反比例函数概念,能画出反比例函数的图像,并结合图像分析总结出反比例函数的性质;
2、通过参与课堂活动,初步领会数形结合的数学思想及普遍联系的辨证唯物主义思想;
教学重点及难点
1、描点画出反比例函数的图像,
2、结合图像分析总结出反比例函数的性质
教具/学具:课件、工作单
教学过程:
教学环节
教师活动
学生活动
设计意图
复习引入
师:什么叫正比例函数?师:如何画正比例函数的图像?正比例函数有什么性质?(强调画函数图像的步骤)师:什么叫反比例函数?(板书:反比例函数,(
k是常数,))师:那么如何画反比例函数的图像呢?反比例函数有什么性质?这就是我们今天我学习的内容。板书:18.3(2)反比例函数的图像与性质
生:解析式形如(k是不等于零的常数)叫做正比例函数。生:用“描点法”画正比例函数的图像。共分三步骤:列表、描点、连线。正比例函数的性质:(1)当k>0时,正比例函数的图像经过第一、三象限;y的值随着x的增大而增大.(2)当k<0时,正比例函数的图像经过第二、四象限;y的值也随着x的增大而减小.解析式形如,(
k为不等于零的常数)叫做反比例函数。
通过回忆已经学过的正比例函数的图像与性质,从而很自然的引出如何画反比例函数的图像以及反比例函数的图像有哪些性质,起到了较好的过渡作用。
新课探索
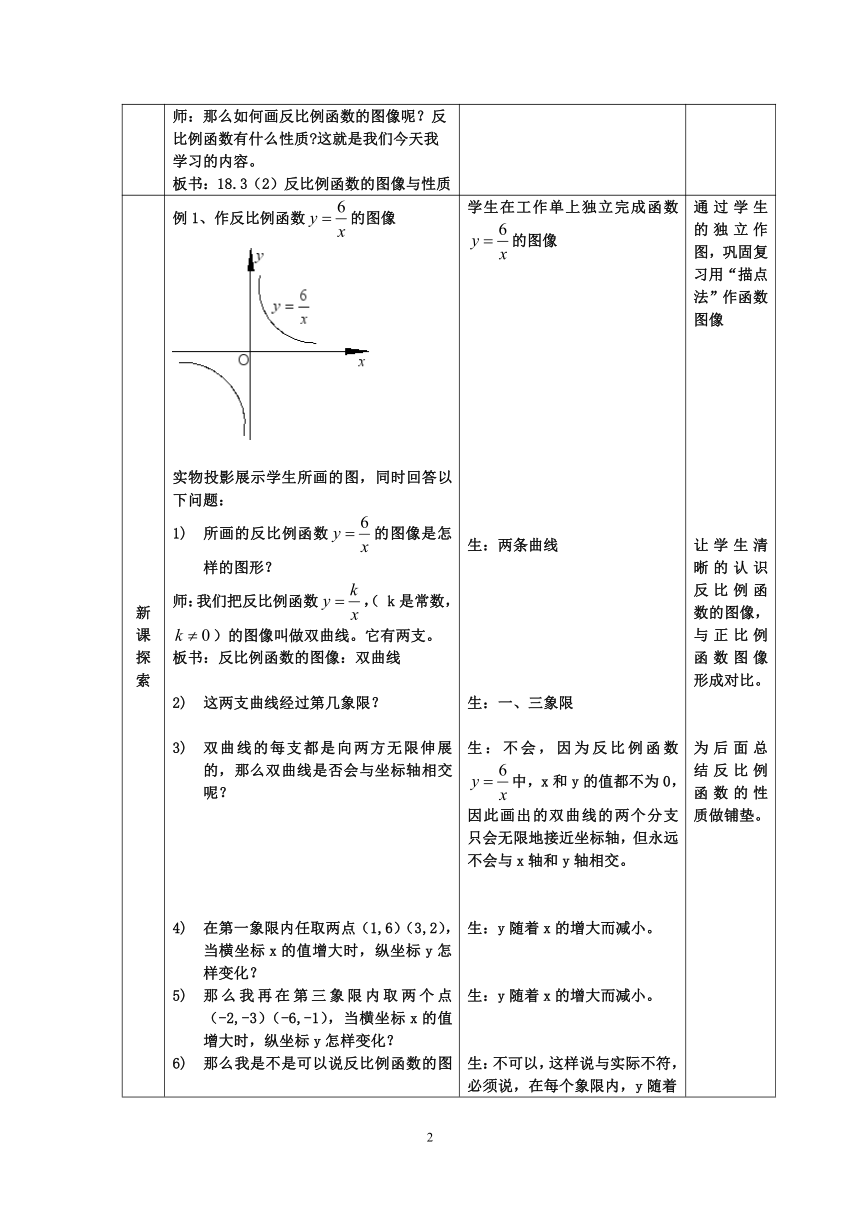
例1、作反比例函数的图像实物投影展示学生所画的图,同时回答以下问题:所画的反比例函数的图像是怎样的图形?师:我们把反比例函数,(
k是常数,)的图像叫做双曲线。它有两支。板书:反比例函数的图像:双曲线这两支曲线经过第几象限?双曲线的每支都是向两方无限伸展的,那么双曲线是否会与坐标轴相交呢?在第一象限内任取两点(1,6)(3,2),当横坐标x的值增大时,纵坐标y怎样变化?那么我再在第三象限内取两个点(-2,-3)(-6,-1),当横坐标x的值增大时,纵坐标y怎样变化?那么我是不是可以说反比例函数的图像双曲线具有如下性质:y随着x的增大而减小?教师用几何画板画出反比例函数的图像。所画的反比例函数的图像是怎样的图形?这两支曲线经过第几象限?双曲线的每支都是向两方无限伸展的,那么双曲线是否会与坐标轴相交呢?在第一象限内任取两点(1,-6)(3,-2),当横坐标x的值增大时,纵坐标y怎样变化?那么我再在第三象限内取两个点(-2,3)(-6,1),当横坐标x的值增大时,纵坐标y怎样变化?那么我是不是可以说反比例函数的图像具有如下性质:y随着x的增大而增大?对比反比例函数和的图像,说能类比正比例函数的性质来说一说反比例函数,(
k是常数,)的性质?
学生在工作单上独立完成函数的图像生:两条曲线生:一、三象限生:不会,因为反比例函数中,x和y的值都不为0,因此画出的双曲线的两个分支只会无限地接近坐标轴,但永远不会与x轴和y轴相交。生:y随着x的增大而减小。生:y随着x的增大而减小。生:不可以,这样说与实际不符,必须说,在每个象限内,y随着x的增大而减小。生:双曲线生:二、四象限。生:不会生:y随着x的增大而增大生:y随着x的增大而增大生:不可以,这样说与实际不符,必须说,在每个象限内,y随着x的增大而增大。生:(1)当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;(2)当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。(3)两个分支都无限接近但永远不能达到x轴和y轴。
通过学生的独立作图,巩固复习用“描点法”作函数图像让学生清晰的认识反比例函数的图像,与正比例函数图像形成对比。为后面总结反比例函数的性质做铺垫。锻炼学生的语言表达能力和概括能力。
巩固练习
已知下列反比例函数:,,,④其中,图像位于第二、四象限的函数是
;在其图像所在的每个象限内,y的值随着x的值增大而减小的函数是
。如果反比例函数的图像在第二、四象限,那么正比例函数的图像经过哪几个象限?已知点在上,若,比较大小.在函数的图像上有三点,则的大小关系为(
)。B、C、
D、
生:②③④生:①生:二、四象限生:生:C
通过练习,巩固反比例函数的性质
本课小结
师:本节课你共有哪些收获?
反比例函数的图像是双曲线。反比例函数的性质:(1)当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;(2)当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。(3)两个分支都无限接近但永远不能达到x轴和y轴。
通过让学生进行总结,让学生对反比例函数的图像及其性质有更深刻的认识与理解。
拓展练习
1、已知点在函数的图像上,求k的值。2、已知点(m,n)在第二象限,那么直线经过第
象限,双曲线的两支在第
象限。3、已知2,4,m是三角形的三边长,那么直线经过第
象限,双曲线的两支在第
象限。4、如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,
4
).(1)分别写出这两个函数的表达式;(2)你能求出点B的坐标吗?你是怎样求的?与同伴交流.
作业布置:练习册18.3(2)板书设计:18.3(2)
反比例函数的图像与性质
反比例函数,(
k是常数,)图像(双曲线)K的符号K>0K<0性质当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。
1
教学目标
1、巩固反比例函数概念,能画出反比例函数的图像,并结合图像分析总结出反比例函数的性质;
2、通过参与课堂活动,初步领会数形结合的数学思想及普遍联系的辨证唯物主义思想;
教学重点及难点
1、描点画出反比例函数的图像,
2、结合图像分析总结出反比例函数的性质
教具/学具:课件、工作单
教学过程:
教学环节
教师活动
学生活动
设计意图
复习引入
师:什么叫正比例函数?师:如何画正比例函数的图像?正比例函数有什么性质?(强调画函数图像的步骤)师:什么叫反比例函数?(板书:反比例函数,(
k是常数,))师:那么如何画反比例函数的图像呢?反比例函数有什么性质?这就是我们今天我学习的内容。板书:18.3(2)反比例函数的图像与性质
生:解析式形如(k是不等于零的常数)叫做正比例函数。生:用“描点法”画正比例函数的图像。共分三步骤:列表、描点、连线。正比例函数的性质:(1)当k>0时,正比例函数的图像经过第一、三象限;y的值随着x的增大而增大.(2)当k<0时,正比例函数的图像经过第二、四象限;y的值也随着x的增大而减小.解析式形如,(
k为不等于零的常数)叫做反比例函数。
通过回忆已经学过的正比例函数的图像与性质,从而很自然的引出如何画反比例函数的图像以及反比例函数的图像有哪些性质,起到了较好的过渡作用。
新课探索
例1、作反比例函数的图像实物投影展示学生所画的图,同时回答以下问题:所画的反比例函数的图像是怎样的图形?师:我们把反比例函数,(
k是常数,)的图像叫做双曲线。它有两支。板书:反比例函数的图像:双曲线这两支曲线经过第几象限?双曲线的每支都是向两方无限伸展的,那么双曲线是否会与坐标轴相交呢?在第一象限内任取两点(1,6)(3,2),当横坐标x的值增大时,纵坐标y怎样变化?那么我再在第三象限内取两个点(-2,-3)(-6,-1),当横坐标x的值增大时,纵坐标y怎样变化?那么我是不是可以说反比例函数的图像双曲线具有如下性质:y随着x的增大而减小?教师用几何画板画出反比例函数的图像。所画的反比例函数的图像是怎样的图形?这两支曲线经过第几象限?双曲线的每支都是向两方无限伸展的,那么双曲线是否会与坐标轴相交呢?在第一象限内任取两点(1,-6)(3,-2),当横坐标x的值增大时,纵坐标y怎样变化?那么我再在第三象限内取两个点(-2,3)(-6,1),当横坐标x的值增大时,纵坐标y怎样变化?那么我是不是可以说反比例函数的图像具有如下性质:y随着x的增大而增大?对比反比例函数和的图像,说能类比正比例函数的性质来说一说反比例函数,(
k是常数,)的性质?
学生在工作单上独立完成函数的图像生:两条曲线生:一、三象限生:不会,因为反比例函数中,x和y的值都不为0,因此画出的双曲线的两个分支只会无限地接近坐标轴,但永远不会与x轴和y轴相交。生:y随着x的增大而减小。生:y随着x的增大而减小。生:不可以,这样说与实际不符,必须说,在每个象限内,y随着x的增大而减小。生:双曲线生:二、四象限。生:不会生:y随着x的增大而增大生:y随着x的增大而增大生:不可以,这样说与实际不符,必须说,在每个象限内,y随着x的增大而增大。生:(1)当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;(2)当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。(3)两个分支都无限接近但永远不能达到x轴和y轴。
通过学生的独立作图,巩固复习用“描点法”作函数图像让学生清晰的认识反比例函数的图像,与正比例函数图像形成对比。为后面总结反比例函数的性质做铺垫。锻炼学生的语言表达能力和概括能力。
巩固练习
已知下列反比例函数:,,,④其中,图像位于第二、四象限的函数是
;在其图像所在的每个象限内,y的值随着x的值增大而减小的函数是
。如果反比例函数的图像在第二、四象限,那么正比例函数的图像经过哪几个象限?已知点在上,若,比较大小.在函数的图像上有三点,则的大小关系为(
)。B、C、
D、
生:②③④生:①生:二、四象限生:生:C
通过练习,巩固反比例函数的性质
本课小结
师:本节课你共有哪些收获?
反比例函数的图像是双曲线。反比例函数的性质:(1)当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;(2)当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。(3)两个分支都无限接近但永远不能达到x轴和y轴。
通过让学生进行总结,让学生对反比例函数的图像及其性质有更深刻的认识与理解。
拓展练习
1、已知点在函数的图像上,求k的值。2、已知点(m,n)在第二象限,那么直线经过第
象限,双曲线的两支在第
象限。3、已知2,4,m是三角形的三边长,那么直线经过第
象限,双曲线的两支在第
象限。4、如图,正比例函数的图象与反比例函数的图象相交于A、B两点,其中点A的坐标为(3,
4
).(1)分别写出这两个函数的表达式;(2)你能求出点B的坐标吗?你是怎样求的?与同伴交流.
作业布置:练习册18.3(2)板书设计:18.3(2)
反比例函数的图像与性质
反比例函数,(
k是常数,)图像(双曲线)K的符号K>0K<0性质当>0时,函数图像的两个分支分别分布在第一、三象限内,在每一个象限中,y随x的增大而减小;当<0时,函数图像的两个分支分别分布在第二、四象限内,在每一个象限中,y随x的增大而增大。
1
