沪教版(上海)数学七年级下册-12.1 实数的概念 教案
文档属性
| 名称 | 沪教版(上海)数学七年级下册-12.1 实数的概念 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览



文档简介
[文档标题]
课题名称:
实数的概念
学科:
数学
授课教师:
班级:
学生人数:
授课时间:
课型分析:概念型课概念是数学知识中最普通的形式,是数学内容的基本点;是逻辑导出定理、公式、性质、法则的出发点;是建立学生认知结构的着眼点。所以概念的学习是数学学习的核心,概念课的教学是教师落实基础的关键,是学生打好基础的首要环节。
教学目标:1.通过动手操作体验发现无理数的过程,知道无理数是客观存在的数.
2.通过对比分析,理解无理数只能是无限不循环小数,会辨别无理数.
3.了解数的范围从整数到有理数、再到实数的扩展过程,知道实数的分类,体会分类的数学思想.
4.了解无理数的发展史,以及在数学史上,对无理数的各种定义。
教学重点:
无理数、实数的概念以及实数的分类.教学难点:
有理数与无理数的区别.
课前自主学习任务简述:
无
小组合作学习任务:通过拼图,知道无理数是客观存在的,知道类似于这类数的几何意义.
解决教学难点的深度思维问题:
无理数是没有道理的数吗?
教学设计过程
教师活动
学生活动
教学意图
旧知复习:教师设问:(1)
和
统称为有理数.(2)如果把整数看成是分母为1的分数,那么有理数都可以用统一的形式表示为用两个整数之比表示的分数:(q≠0)引入新课:问1:在现实生活中,是否存在不能用两个整数之比来表示的数呢?让我们带着这个问题,进行探讨:你能用什么办法来求一张A4纸的长与宽的比?生答(预设):通过测量长和宽来求比。师:这样测出来的是否准确呢?(演示折纸过程)问2:通过折纸可以发现,折痕AE和长AD的长度一样,若将AB看做1,AE的长度又是多少呢?
已知正方形ABEF的边AB=1,我们会求什么?
问:面积为1的正方形的边长是多少?面积为4呢?
思考:是否能以AE为边长,构造一个正方形,通过这个正方形的面积,来求AE的长呢?
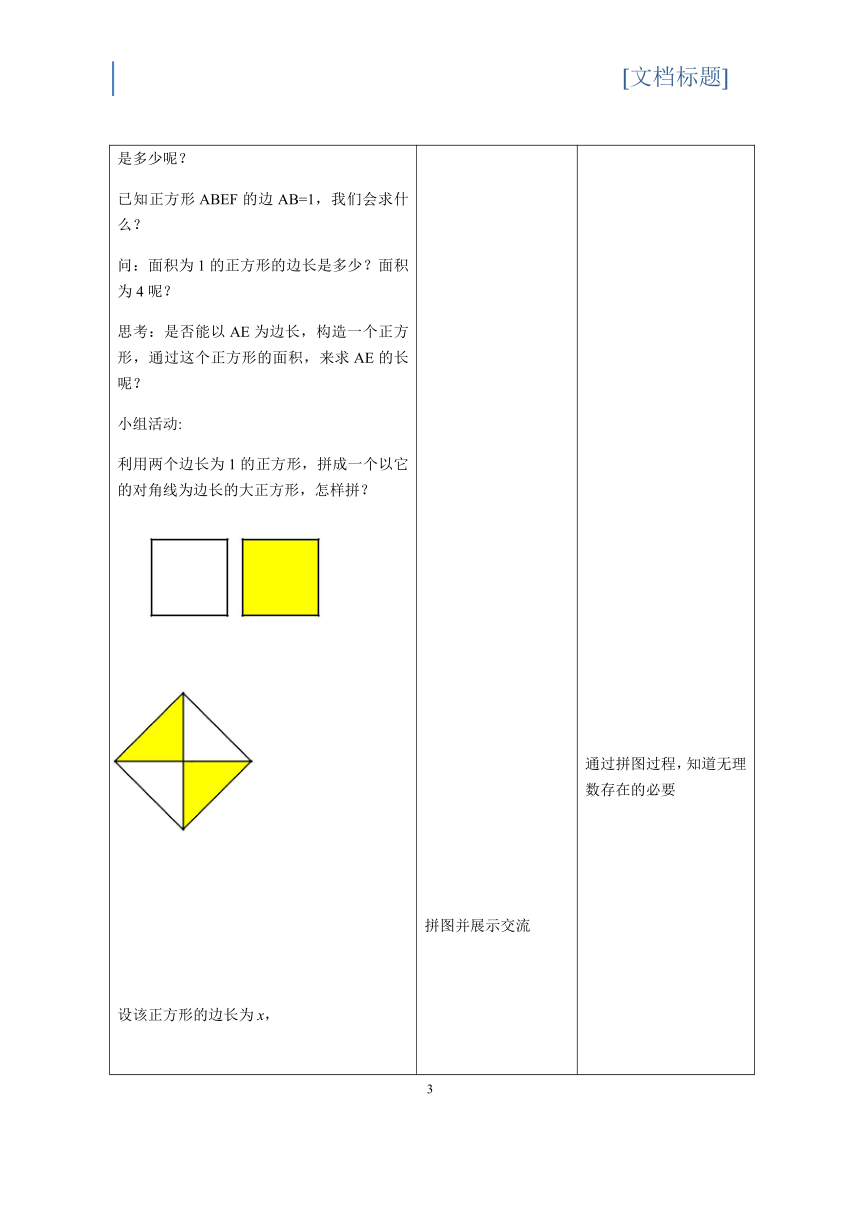
小组活动:利用两个边长为1的正方形,拼成一个以它的对角线为边长的大正方形,怎样拼?设该正方形的边长为x,那.这个x究竟是多少呢?
(学生试算)通过以上的拼图,我们知道,如果将宽当做1,那么长就是,此时长与宽的比就是:1
。(不是我们所学过的整数)这也就说明了不是所有的数都能用两个整数之比来表示,那么他就不是一个分数(不能化成有限小数或无限循环小数),更不是有理数。师:我们给这样的数,起了一个新的名字,叫无理数。你能说说什么叫无理数吗?(三)实数的概念1.无理数无限不循环小数叫做无理数.
在本教材中,无理数是这样定义的。而无理数的发展,却经历了2000多年,通过下面这个视频,让我们穿越时空,回顾一下无理数的发展史。(播放视频:无理数发展史)板书:2.实数板书:有理数和无理数统称为实数.(四)例题讲解例1:将下列各数放入图中适当的位置:0、–2、、3.14、、、、、0.3737737773…(它们的位数无限且相邻两个“3”之间“7”的个数依次加1个).无理数有
,正有理数有
,非正数有
,整数有
.练习:
判断下列说法是否正确,并说明理由:(1)
无限小数都是无理数;
(2)
无理数都是无限小数;(3)
实数可以分为正实数和负实数两类;(4)
有理数是正的和负的整数和分数,
其他实数都称为无理数.解:(1)无限小数包括无限循环小数和无限不循环小数,其中无限循环小数是有理数,所以(1)不正确.
(2)无理数是无限不循环小数,当然也是无限小数,所以(2)正确.
(3)因为零是实数,但它既不是正实数,也不是负实数,而在(3)的实数分类中没有把零包含在内,所以不正确(4)正的和负的整数和分数没有包括0,而0是有理数,所以(4)正确.【适时小结】实数还可以这样分类:(五)课堂小结通过本节课的学习,你有了那些收获?
本节课,给你留下了深刻印象的是那部分内容?
(六)布置作业
整数,分数动手操作拼图并展示交流总结特点,得出概念观看视频熟知分类思考并回答判定并说出理由交流心得体会
通过复习,引出问题,进行探究。通过动手操作体验发现无理数的过程,知道无理数是客观存在的数通过拼图过程,知道无理数存在的必要了解无理数发展史知道实数的分类,体会分类的数学思想运用概念解决问题概念辨析,熟练掌握交流感悟,情感提升
课后反思:
整体觉得比较顺畅,尤其是有A4纸的折纸到拼正方形的过度,显得比较顺畅自然。对于微视频介绍数学史,这也算是一个新的尝试,效果觉得还不错,学生印象非常深刻。根号2的几何意义,给学生留下了深刻的印象,也为后续的教学奠定了基础。和常规课相比较,这样的课更能吸引学生,使学生作为学习的主体,参与到课堂学习中。概念教学本来就是比较枯燥乏味的,引入数学史后,不仅丰富了学生的知识,还活跃了课堂氛围,一举多得。相对练习较少,部分学生对与类型题的要求不是很理解,但这也可以通过后续的学习得以弥补。学科德育方面:学生了解了数学史,知道了无理数发展的艰辛,我们现在,仅仅利用1节课的时间,就完成了2000多年的穿越,从情感上,存在一种自豪感。另外,知道了历史中的一些定义,原来也是错误的,经过上百年才得以改正,也使学生正视一个问题,我们都会犯错,但无论过程多曲折,错误就是错误,经不起事实的考验,终要改正。从另一个角度来说,这种钻研的精神,更是当代学生所缺乏的,也是值得他们学习的。
5
课题名称:
实数的概念
学科:
数学
授课教师:
班级:
学生人数:
授课时间:
课型分析:概念型课概念是数学知识中最普通的形式,是数学内容的基本点;是逻辑导出定理、公式、性质、法则的出发点;是建立学生认知结构的着眼点。所以概念的学习是数学学习的核心,概念课的教学是教师落实基础的关键,是学生打好基础的首要环节。
教学目标:1.通过动手操作体验发现无理数的过程,知道无理数是客观存在的数.
2.通过对比分析,理解无理数只能是无限不循环小数,会辨别无理数.
3.了解数的范围从整数到有理数、再到实数的扩展过程,知道实数的分类,体会分类的数学思想.
4.了解无理数的发展史,以及在数学史上,对无理数的各种定义。
教学重点:
无理数、实数的概念以及实数的分类.教学难点:
有理数与无理数的区别.
课前自主学习任务简述:
无
小组合作学习任务:通过拼图,知道无理数是客观存在的,知道类似于这类数的几何意义.
解决教学难点的深度思维问题:
无理数是没有道理的数吗?
教学设计过程
教师活动
学生活动
教学意图
旧知复习:教师设问:(1)
和
统称为有理数.(2)如果把整数看成是分母为1的分数,那么有理数都可以用统一的形式表示为用两个整数之比表示的分数:(q≠0)引入新课:问1:在现实生活中,是否存在不能用两个整数之比来表示的数呢?让我们带着这个问题,进行探讨:你能用什么办法来求一张A4纸的长与宽的比?生答(预设):通过测量长和宽来求比。师:这样测出来的是否准确呢?(演示折纸过程)问2:通过折纸可以发现,折痕AE和长AD的长度一样,若将AB看做1,AE的长度又是多少呢?
已知正方形ABEF的边AB=1,我们会求什么?
问:面积为1的正方形的边长是多少?面积为4呢?
思考:是否能以AE为边长,构造一个正方形,通过这个正方形的面积,来求AE的长呢?
小组活动:利用两个边长为1的正方形,拼成一个以它的对角线为边长的大正方形,怎样拼?设该正方形的边长为x,那.这个x究竟是多少呢?
(学生试算)通过以上的拼图,我们知道,如果将宽当做1,那么长就是,此时长与宽的比就是:1
。(不是我们所学过的整数)这也就说明了不是所有的数都能用两个整数之比来表示,那么他就不是一个分数(不能化成有限小数或无限循环小数),更不是有理数。师:我们给这样的数,起了一个新的名字,叫无理数。你能说说什么叫无理数吗?(三)实数的概念1.无理数无限不循环小数叫做无理数.
在本教材中,无理数是这样定义的。而无理数的发展,却经历了2000多年,通过下面这个视频,让我们穿越时空,回顾一下无理数的发展史。(播放视频:无理数发展史)板书:2.实数板书:有理数和无理数统称为实数.(四)例题讲解例1:将下列各数放入图中适当的位置:0、–2、、3.14、、、、、0.3737737773…(它们的位数无限且相邻两个“3”之间“7”的个数依次加1个).无理数有
,正有理数有
,非正数有
,整数有
.练习:
判断下列说法是否正确,并说明理由:(1)
无限小数都是无理数;
(2)
无理数都是无限小数;(3)
实数可以分为正实数和负实数两类;(4)
有理数是正的和负的整数和分数,
其他实数都称为无理数.解:(1)无限小数包括无限循环小数和无限不循环小数,其中无限循环小数是有理数,所以(1)不正确.
(2)无理数是无限不循环小数,当然也是无限小数,所以(2)正确.
(3)因为零是实数,但它既不是正实数,也不是负实数,而在(3)的实数分类中没有把零包含在内,所以不正确(4)正的和负的整数和分数没有包括0,而0是有理数,所以(4)正确.【适时小结】实数还可以这样分类:(五)课堂小结通过本节课的学习,你有了那些收获?
本节课,给你留下了深刻印象的是那部分内容?
(六)布置作业
整数,分数动手操作拼图并展示交流总结特点,得出概念观看视频熟知分类思考并回答判定并说出理由交流心得体会
通过复习,引出问题,进行探究。通过动手操作体验发现无理数的过程,知道无理数是客观存在的数通过拼图过程,知道无理数存在的必要了解无理数发展史知道实数的分类,体会分类的数学思想运用概念解决问题概念辨析,熟练掌握交流感悟,情感提升
课后反思:
整体觉得比较顺畅,尤其是有A4纸的折纸到拼正方形的过度,显得比较顺畅自然。对于微视频介绍数学史,这也算是一个新的尝试,效果觉得还不错,学生印象非常深刻。根号2的几何意义,给学生留下了深刻的印象,也为后续的教学奠定了基础。和常规课相比较,这样的课更能吸引学生,使学生作为学习的主体,参与到课堂学习中。概念教学本来就是比较枯燥乏味的,引入数学史后,不仅丰富了学生的知识,还活跃了课堂氛围,一举多得。相对练习较少,部分学生对与类型题的要求不是很理解,但这也可以通过后续的学习得以弥补。学科德育方面:学生了解了数学史,知道了无理数发展的艰辛,我们现在,仅仅利用1节课的时间,就完成了2000多年的穿越,从情感上,存在一种自豪感。另外,知道了历史中的一些定义,原来也是错误的,经过上百年才得以改正,也使学生正视一个问题,我们都会犯错,但无论过程多曲折,错误就是错误,经不起事实的考验,终要改正。从另一个角度来说,这种钻研的精神,更是当代学生所缺乏的,也是值得他们学习的。
5
