沪教版(上海)数学八年级第二学期-22.1 多边形的内角和 课件(共19张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.1 多边形的内角和 课件(共19张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 469.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览

文档简介
(共19张PPT)
22.1
多边形的内角和
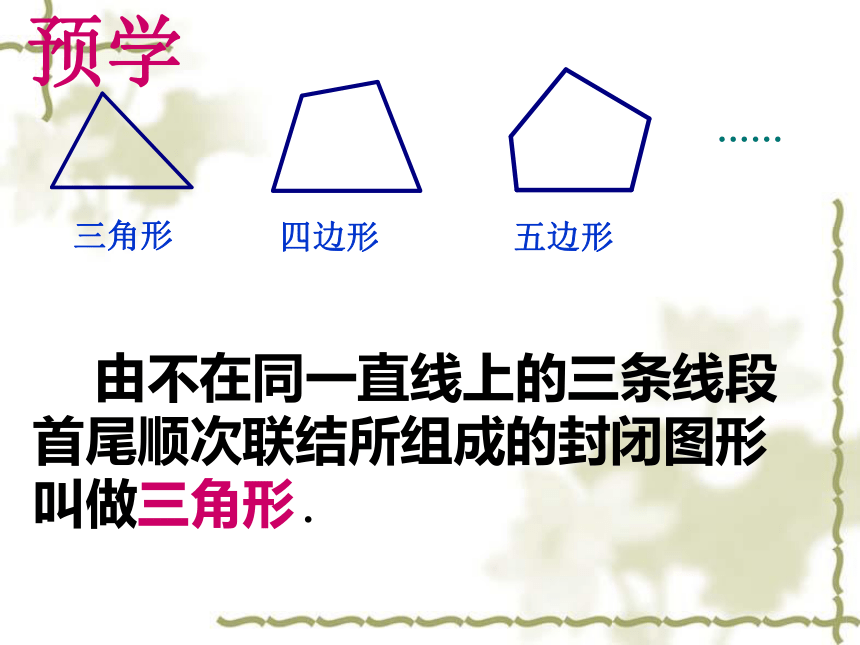
三角形
四边形
五边形
……
由不在同一直线上的三条线段首尾顺次联结所组成的封闭图形叫做三角形.
预学
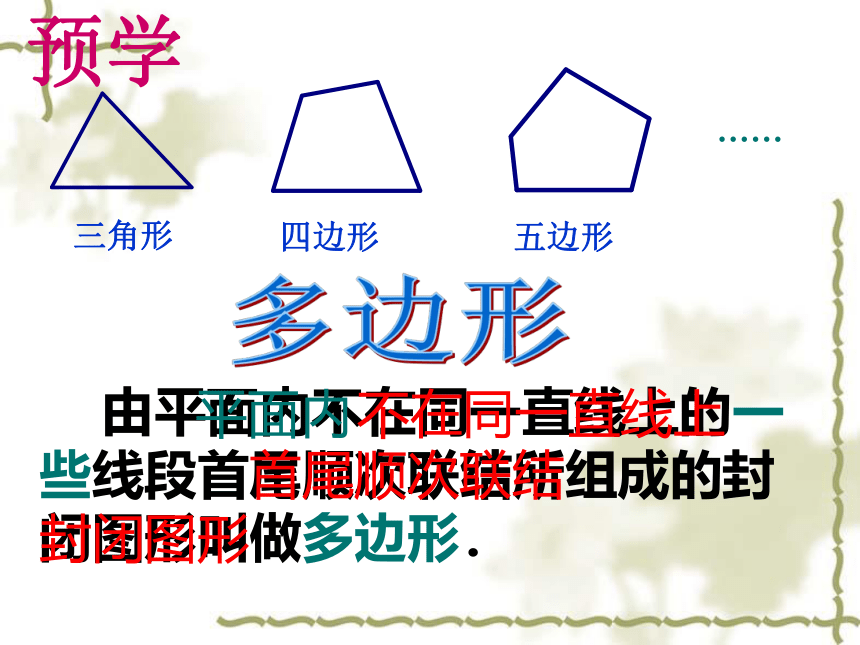
三角形
四边形
五边形
多边形
……
由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.
不在同一直线上
首尾顺次联结
封闭图形
平面内
预学
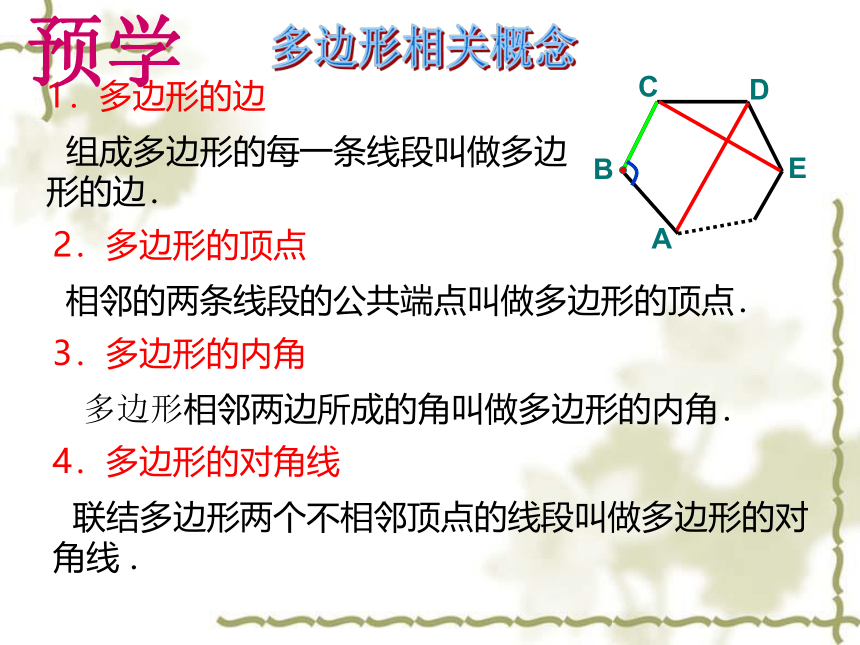
1.多边形的边
组成多边形的每一条线段叫做多边形的边.
2.多边形的顶点
相邻的两条线段的公共端点叫做多边形的顶点.
3.多边形的内角
多边形相邻两边所成的角叫做多边形的内角.
4.多边形的对角线
联结多边形两个不相邻顶点的线段叫做多边形的对角线
.
B
A
D
E
C
多边形相关概念
预学
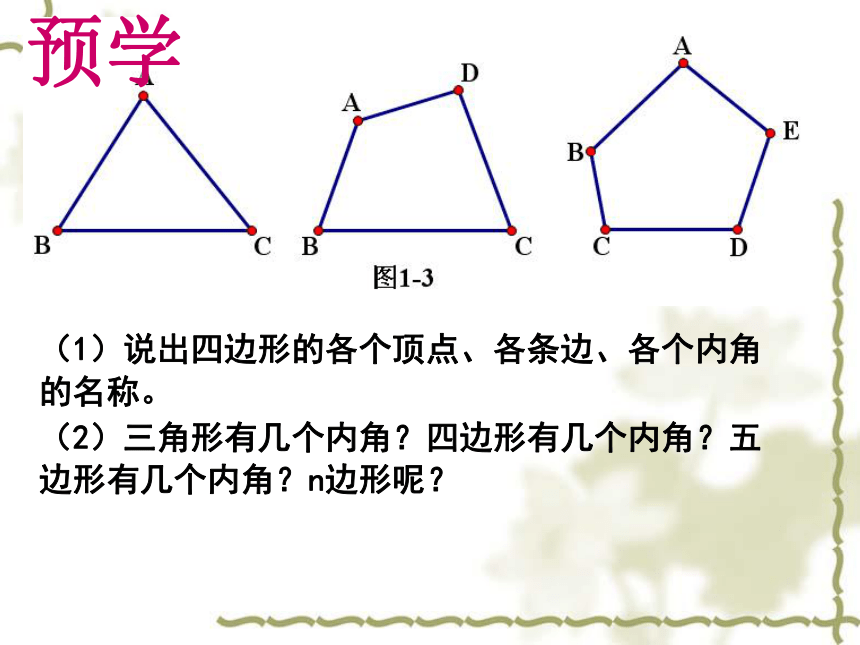
(1)说出四边形的各个顶点、各条边、各个内角的名称。
(2)三角形有几个内角?四边形有几个内角?五边形有几个内角?n边形呢?
预学
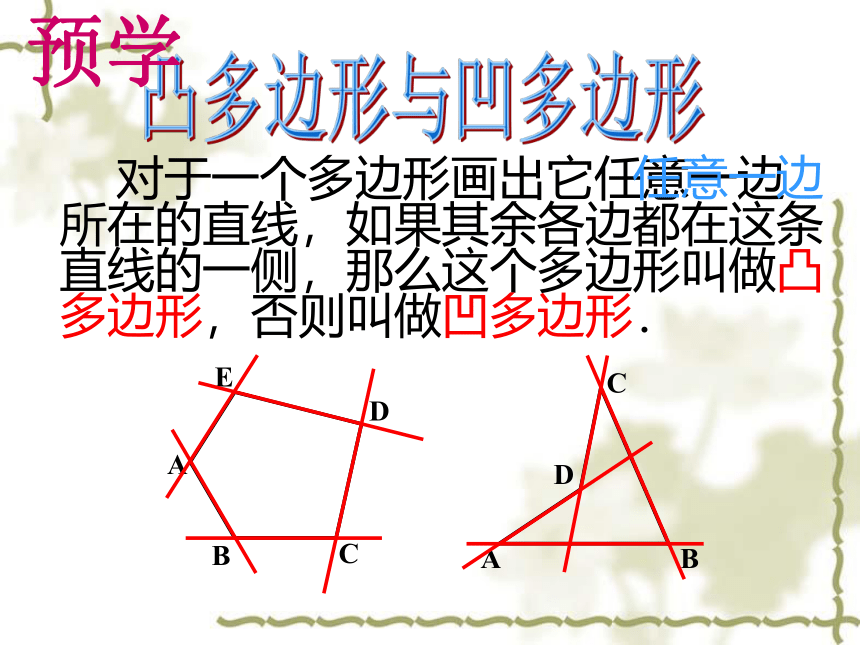
对于一个多边形画出它任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形,否则叫做凹多边形.
凸多边形与凹多边形
B
A
C
D
E
D
A
B
C
任意一边
预学
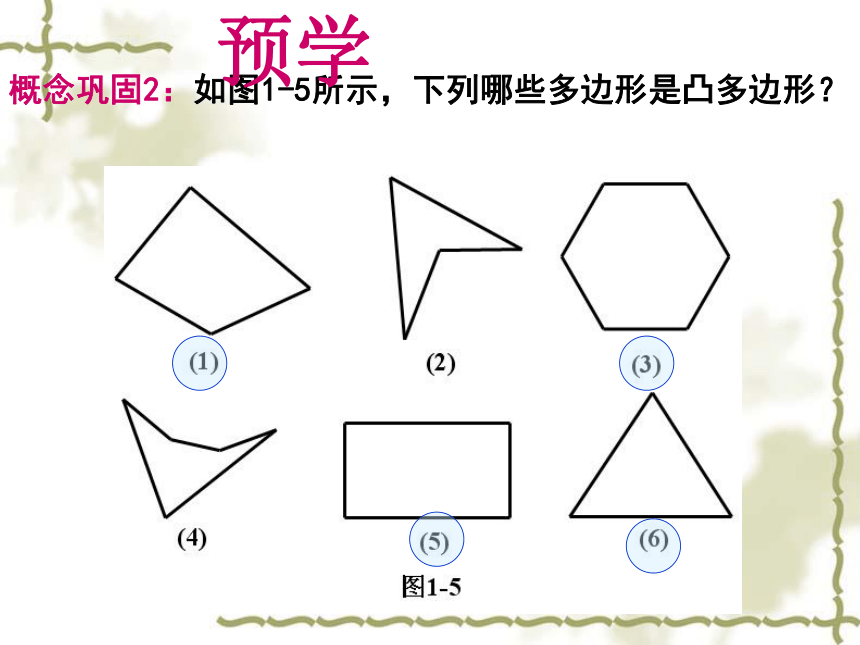
概念巩固2:如图1-5所示,下列哪些多边形是凸多边形?
预学
生活中的多边形
A
B
C
D
四边形的对角线共有几条?
A
B
C
D
E
五边形的对角线共有几条?
A
B
C
(3)三角形有对角线吗?
三角形的内角和为180°
探索与归纳:
多边形的内角和
边形的内角和为几度?
不同的分割方法
方法1
方法2
方法3
将五边形ABCDE分割成多个三角形
五边形ABCDE内角和的度数计算
3×180°=
540°
4×180°-180°
=
540°
5×180°-360°
=
540°
从多边形一个顶点出发的对角线可以将这个多边形分成若干个三角形
多边形
的边数
图
形
从一个顶点出发的对角线条数
分割出的三角形的个数
多边形的
内
角
和
4
5
6
n
n-2
2
3
2×180?
3×180?
(n-2)×180?
1
2
n-3
…
…
…
…
…
4
4×180?
3
归纳3:多边形的内角和定理
n边形的内角和等于(n-2)·180°
想一想:如果多边形的边数增加1,那么这个多边形的内角和增加多少度呢?
例题1:求十二边形内角和.
例题2:已知一个多边形的内角和为2160°,求这个多边形的边数
。
动手动脑:有一块长方形的纸片,把它减去一个角后所成的多边形纸片的内角和可能是多少度?
例题3:已知多边形的每一个内角都等于150°,问这个多边形是几边形?
1.
多边形的有关概念;
2.
多边形的内角和公式
n边形的内角和
=(n-2)?
180?;
3.
类比、转化的数学思想方法.
小结
作业
1.练习册:22.1(1)
一个多边形除了一个内角等于α,其余角的和等于700°,求这个多边形的边数,及α的值.
2.思考题:
22.1
多边形的内角和
三角形
四边形
五边形
……
由不在同一直线上的三条线段首尾顺次联结所组成的封闭图形叫做三角形.
预学
三角形
四边形
五边形
多边形
……
由平面内不在同一直线上的一些线段首尾顺次联结所组成的封闭图形叫做多边形.
不在同一直线上
首尾顺次联结
封闭图形
平面内
预学
1.多边形的边
组成多边形的每一条线段叫做多边形的边.
2.多边形的顶点
相邻的两条线段的公共端点叫做多边形的顶点.
3.多边形的内角
多边形相邻两边所成的角叫做多边形的内角.
4.多边形的对角线
联结多边形两个不相邻顶点的线段叫做多边形的对角线
.
B
A
D
E
C
多边形相关概念
预学
(1)说出四边形的各个顶点、各条边、各个内角的名称。
(2)三角形有几个内角?四边形有几个内角?五边形有几个内角?n边形呢?
预学
对于一个多边形画出它任意一边所在的直线,如果其余各边都在这条直线的一侧,那么这个多边形叫做凸多边形,否则叫做凹多边形.
凸多边形与凹多边形
B
A
C
D
E
D
A
B
C
任意一边
预学
概念巩固2:如图1-5所示,下列哪些多边形是凸多边形?
预学
生活中的多边形
A
B
C
D
四边形的对角线共有几条?
A
B
C
D
E
五边形的对角线共有几条?
A
B
C
(3)三角形有对角线吗?
三角形的内角和为180°
探索与归纳:
多边形的内角和
边形的内角和为几度?
不同的分割方法
方法1
方法2
方法3
将五边形ABCDE分割成多个三角形
五边形ABCDE内角和的度数计算
3×180°=
540°
4×180°-180°
=
540°
5×180°-360°
=
540°
从多边形一个顶点出发的对角线可以将这个多边形分成若干个三角形
多边形
的边数
图
形
从一个顶点出发的对角线条数
分割出的三角形的个数
多边形的
内
角
和
4
5
6
n
n-2
2
3
2×180?
3×180?
(n-2)×180?
1
2
n-3
…
…
…
…
…
4
4×180?
3
归纳3:多边形的内角和定理
n边形的内角和等于(n-2)·180°
想一想:如果多边形的边数增加1,那么这个多边形的内角和增加多少度呢?
例题1:求十二边形内角和.
例题2:已知一个多边形的内角和为2160°,求这个多边形的边数
。
动手动脑:有一块长方形的纸片,把它减去一个角后所成的多边形纸片的内角和可能是多少度?
例题3:已知多边形的每一个内角都等于150°,问这个多边形是几边形?
1.
多边形的有关概念;
2.
多边形的内角和公式
n边形的内角和
=(n-2)?
180?;
3.
类比、转化的数学思想方法.
小结
作业
1.练习册:22.1(1)
一个多边形除了一个内角等于α,其余角的和等于700°,求这个多边形的边数,及α的值.
2.思考题:
