沪教版(上海)数学八年级第二学期-22.5 (2)等腰梯形的判定 课件(共23张ppt)
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.5 (2)等腰梯形的判定 课件(共23张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 768.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览



文档简介
(共23张PPT)
获取知识的过程
比结果更重要
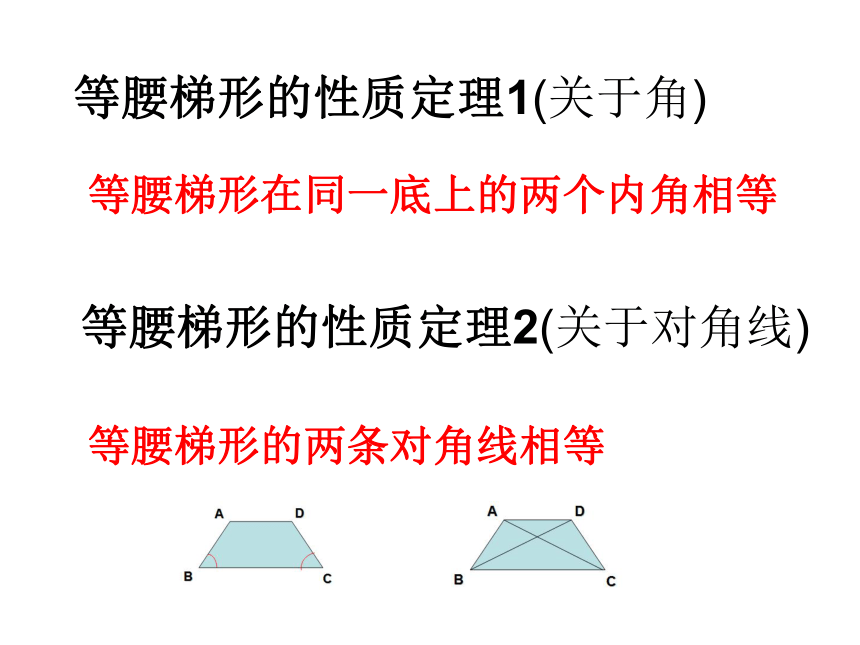
等腰梯形的性质定理1(关于角)
等腰梯形在同一底上的两个内角相等
等腰梯形的性质定理2(关于对角线)
等腰梯形的两条对角线相等
22.5(2)等腰梯形的判定
执教者:张强
平行四边形性质定理1:平行四边形的两组对边分别相等
平行四边形判定定理1:两组对边分别相等的
四边形是平行四边形
下面我们就从等腰梯形的性质入手探索等腰梯形的判定方法
等腰梯形
性
质
逆
命
题
角
对角线
等腰梯形同一底上的两个内角相等
等腰梯形的对角线相等
同一底上的两个内角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
知识回顾
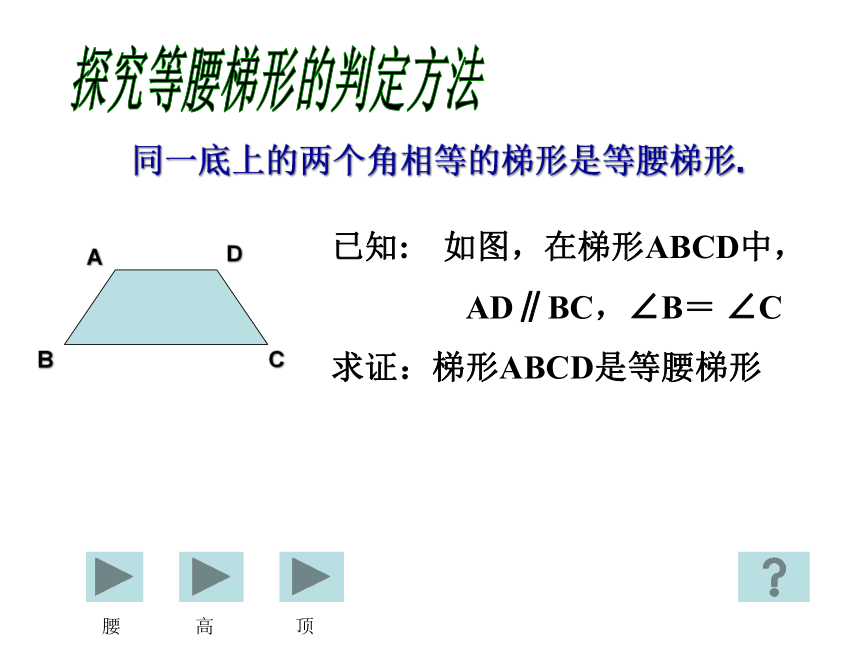
探究等腰梯形的判定方法
A
B
C
D
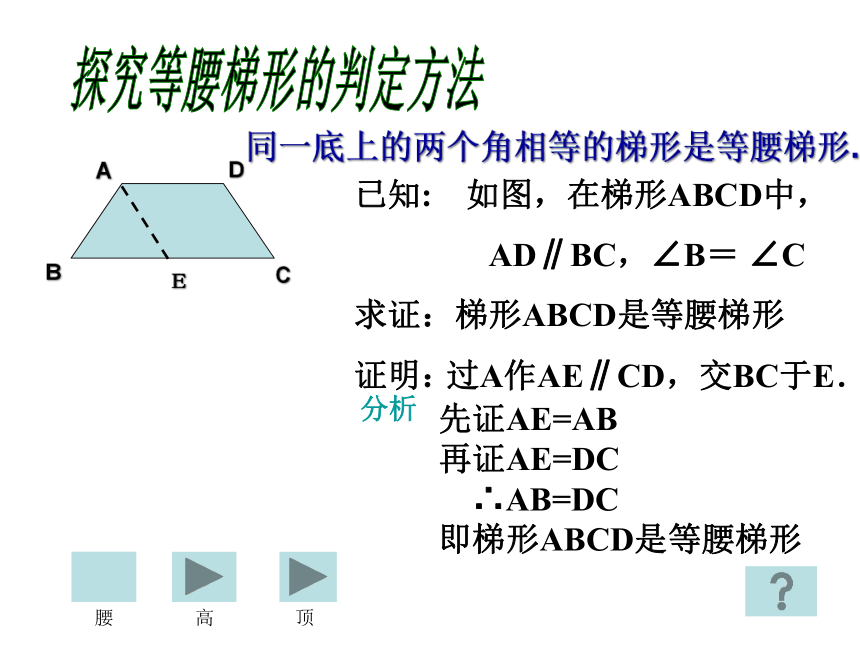
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
腰
高
顶
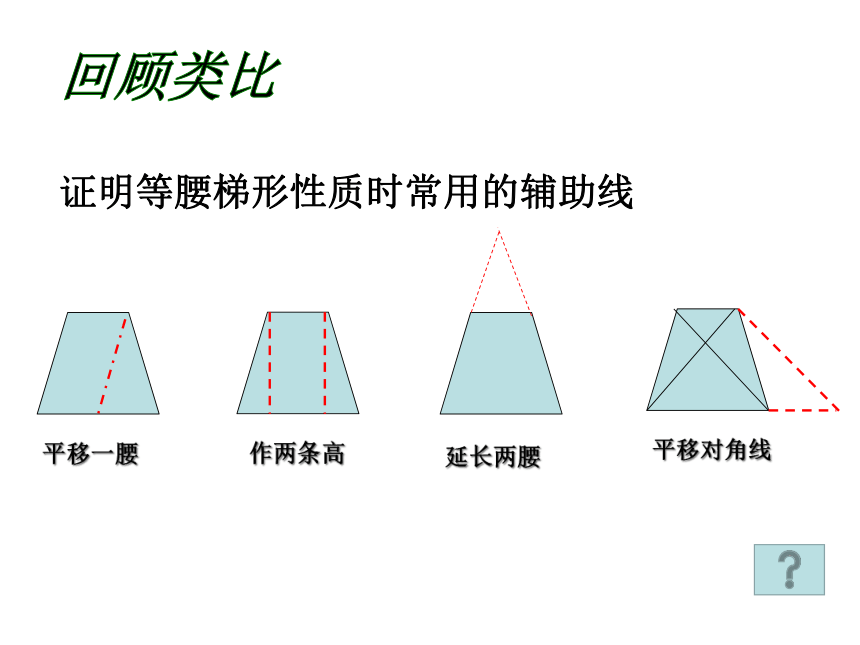
证明等腰梯形性质时常用的辅助线
平移一腰
平移对角线
作两条高
延长两腰
回顾类比
先证AE=AB
再证AE=DC
∴AB=DC
即梯形ABCD是等腰梯形
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
证明:
E
过A作AE∥CD,交BC于E.
分析
腰
高
顶
探究等腰梯形的判定方法
A
B
C
D
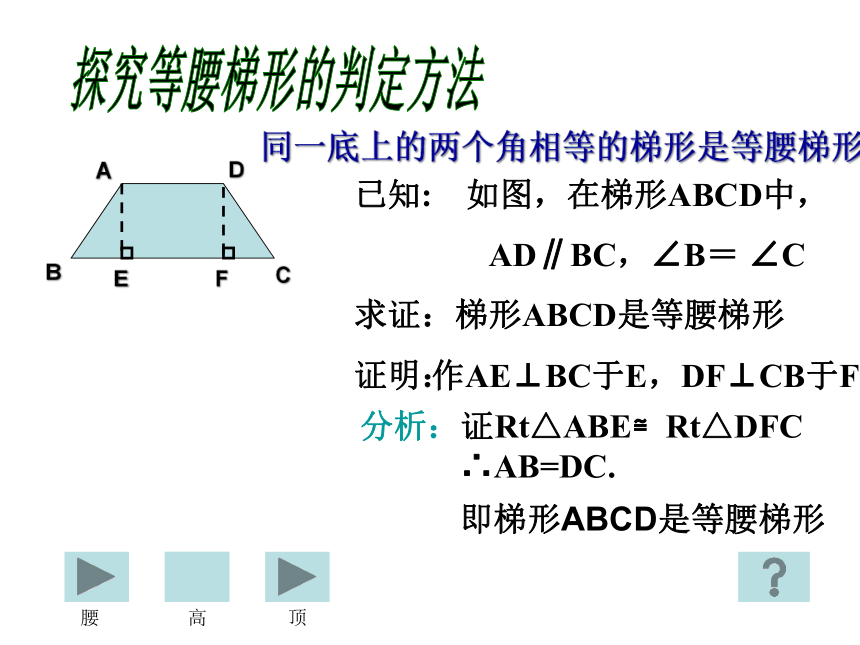
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
证明:
作AE⊥BC于E,DF⊥CB于F
F
分析:证Rt△ABE≌Rt△DFC
∴AB=DC.
E
即梯形ABCD是等腰梯形
腰
高
顶
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
E
先证EB=EC,
再证EA=ED
∴EB-EA=EC-ED
即AB=CD
证明:延长BA、CD交于点E
即梯形ABCD是等腰梯形
分析:
腰
高
顶
(1)做腰平行线
(2)做高
(3)延长两腰
A
D
C
B
A
D
C
B
A
D
C
B
同一底上的两角相等的梯形是等腰梯形
A
B
C
D
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
线
高
A
B
C
D
E
证明:过点D作DE∥AC交BC的延长线于点E
分析:先证DB=DE
易得∠1=∠2
再证△ABC≌△DCB
∴AB=CD
即梯形ABCD是等腰梯形
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
返回
1
2
线
高
再证△ABC≌△DCB
∴AB=CD
A
B
C
D
证明:
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
E
F
作AE⊥BC于点E,
作DF⊥BC于点F
分析:证Rt△AEC≌Rt△DFB
∴∠2=∠1
即梯形ABCD是等腰梯形
返回
1
2
线
高
对角线相等的梯形是等腰梯形
等腰梯形
性
质
判
定
角
对角线
等腰梯形同一底上的两个内角相等
等腰梯形的对角线相等
同一底上的两个内角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
∴梯形ABCD是等腰梯形
(
)
等腰梯形的判定方法
A
B
C
D
同一底上的两个内角相等的
梯形是等腰梯形.
对角线相等的梯形是等腰梯形.
A
B
C
D
符号语言:
在梯形ABCD中,
∵
∴梯形ABCD是等腰梯形
(
)
在梯形ABCD中,
∵
∠B=
∠C
(或∠A=
∠D)
AC=
BD
1.已知梯形ABCD中,
AD∥BC,AB//DE,DE=DC,∠A=110°则
∠B=
;∠C=
;∠ADC=
;
E
C
B
A
D
110°
巩固练习
2、已知:如图,在梯形ABCD中,AB∥DC,点E在边AB的延长线上,且BE=DC,AC=CE
求证:在梯形ABCD是等腰梯形
a
b
c
d
例题5
已知梯形的两底和两腰,求作这个梯形
已知:线段a、b、c、d,其中a>b
求作:梯形ABCD,使AB//DC,
AB=a,DC=b,DA=c,CB=d
B
A
C
D
b
c
d
E
b
a-b
d
三角形奠基法
1、等腰梯形的判定方法:
2、梯形中常用的辅助线
平移一腰
平移对角线
作两条高
延长两腰
小结
3、重要的思想方法——化归
作业:
学习单上课后练习(必做)
学习单上拓展训练(选作)
感谢同学们的配合
同学们再见
获取知识的过程
比结果更重要
等腰梯形的性质定理1(关于角)
等腰梯形在同一底上的两个内角相等
等腰梯形的性质定理2(关于对角线)
等腰梯形的两条对角线相等
22.5(2)等腰梯形的判定
执教者:张强
平行四边形性质定理1:平行四边形的两组对边分别相等
平行四边形判定定理1:两组对边分别相等的
四边形是平行四边形
下面我们就从等腰梯形的性质入手探索等腰梯形的判定方法
等腰梯形
性
质
逆
命
题
角
对角线
等腰梯形同一底上的两个内角相等
等腰梯形的对角线相等
同一底上的两个内角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
知识回顾
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
腰
高
顶
证明等腰梯形性质时常用的辅助线
平移一腰
平移对角线
作两条高
延长两腰
回顾类比
先证AE=AB
再证AE=DC
∴AB=DC
即梯形ABCD是等腰梯形
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
证明:
E
过A作AE∥CD,交BC于E.
分析
腰
高
顶
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
证明:
作AE⊥BC于E,DF⊥CB于F
F
分析:证Rt△ABE≌Rt△DFC
∴AB=DC.
E
即梯形ABCD是等腰梯形
腰
高
顶
探究等腰梯形的判定方法
A
B
C
D
同一底上的两个角相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,
AD∥BC,∠B=
∠C
求证:梯形ABCD是等腰梯形
E
先证EB=EC,
再证EA=ED
∴EB-EA=EC-ED
即AB=CD
证明:延长BA、CD交于点E
即梯形ABCD是等腰梯形
分析:
腰
高
顶
(1)做腰平行线
(2)做高
(3)延长两腰
A
D
C
B
A
D
C
B
A
D
C
B
同一底上的两角相等的梯形是等腰梯形
A
B
C
D
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
线
高
A
B
C
D
E
证明:过点D作DE∥AC交BC的延长线于点E
分析:先证DB=DE
易得∠1=∠2
再证△ABC≌△DCB
∴AB=CD
即梯形ABCD是等腰梯形
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
返回
1
2
线
高
再证△ABC≌△DCB
∴AB=CD
A
B
C
D
证明:
探究等腰梯形的判定方法
对角线相等的梯形是等腰梯形.
已知: 如图,在梯形ABCD中,AD∥BC,AC=BD
求证:梯形ABCD是等腰梯形
E
F
作AE⊥BC于点E,
作DF⊥BC于点F
分析:证Rt△AEC≌Rt△DFB
∴∠2=∠1
即梯形ABCD是等腰梯形
返回
1
2
线
高
对角线相等的梯形是等腰梯形
等腰梯形
性
质
判
定
角
对角线
等腰梯形同一底上的两个内角相等
等腰梯形的对角线相等
同一底上的两个内角相等的梯形是等腰梯形
对角线相等的梯形是等腰梯形
∴梯形ABCD是等腰梯形
(
)
等腰梯形的判定方法
A
B
C
D
同一底上的两个内角相等的
梯形是等腰梯形.
对角线相等的梯形是等腰梯形.
A
B
C
D
符号语言:
在梯形ABCD中,
∵
∴梯形ABCD是等腰梯形
(
)
在梯形ABCD中,
∵
∠B=
∠C
(或∠A=
∠D)
AC=
BD
1.已知梯形ABCD中,
AD∥BC,AB//DE,DE=DC,∠A=110°则
∠B=
;∠C=
;∠ADC=
;
E
C
B
A
D
110°
巩固练习
2、已知:如图,在梯形ABCD中,AB∥DC,点E在边AB的延长线上,且BE=DC,AC=CE
求证:在梯形ABCD是等腰梯形
a
b
c
d
例题5
已知梯形的两底和两腰,求作这个梯形
已知:线段a、b、c、d,其中a>b
求作:梯形ABCD,使AB//DC,
AB=a,DC=b,DA=c,CB=d
B
A
C
D
b
c
d
E
b
a-b
d
三角形奠基法
1、等腰梯形的判定方法:
2、梯形中常用的辅助线
平移一腰
平移对角线
作两条高
延长两腰
小结
3、重要的思想方法——化归
作业:
学习单上课后练习(必做)
学习单上拓展训练(选作)
感谢同学们的配合
同学们再见
