沪教版(上海)数学八年级第二学期-22.6 三角形、梯形的中位线(2) 教案
文档属性
| 名称 | 沪教版(上海)数学八年级第二学期-22.6 三角形、梯形的中位线(2) 教案 |  | |
| 格式 | zip | ||
| 文件大小 | 5.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:47:45 | ||
图片预览

文档简介
§22.6
三角形、梯形的中位线(2)
教学目标:
1.理解梯形的中位线概念,培养数学语言的表达和归纳能力.
2.在探索梯形中位线的性质过程,感受化归的数学思想.
3.掌握梯形中位线的性质定理,能运用定理进行计算和推理论证.
教学重点:梯形中位线性质定理的运用.
教学难点:梯形辅助线的添加.
教学过程:
教师活动
学生活动
教学设计意图
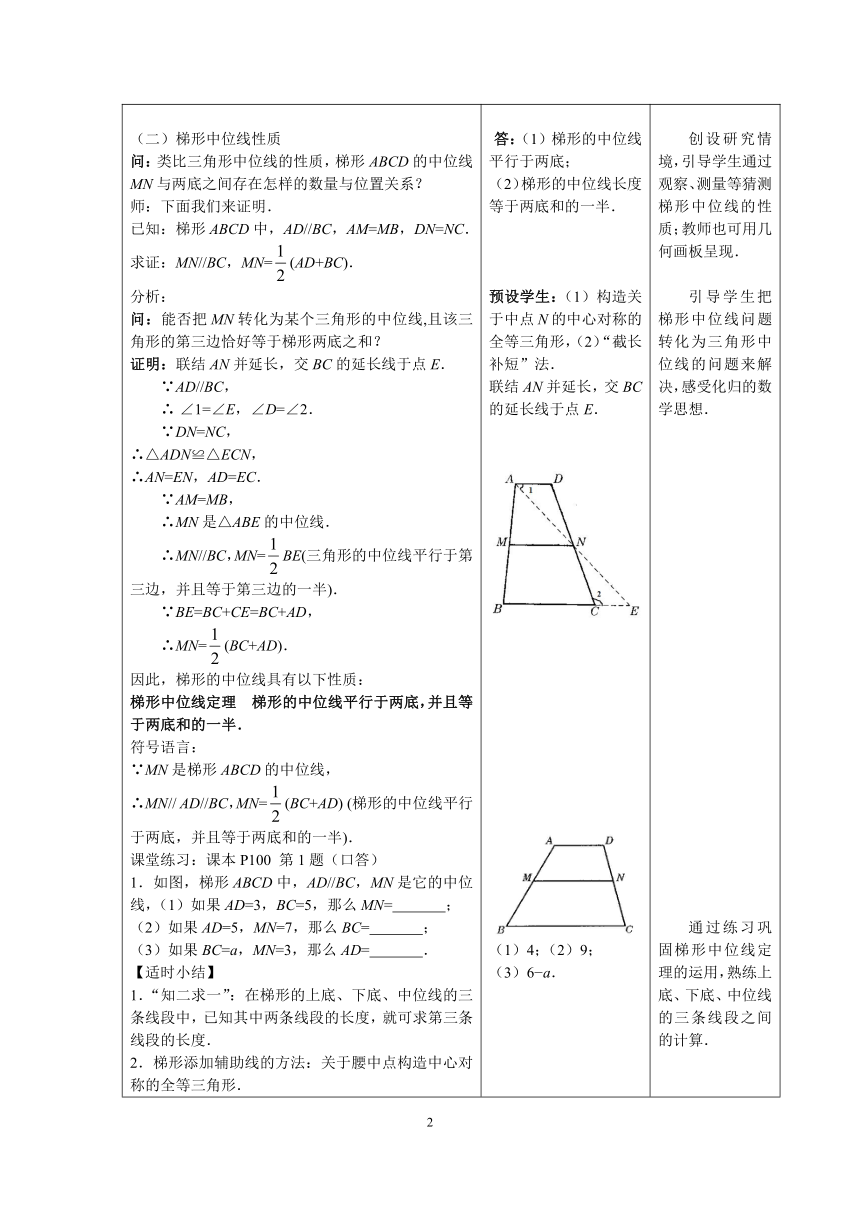
一、复习旧知,导入新课问1:什么叫三角形的中位线?问2:三角形的中位线有什么性质?三角形的中位线是三角形中的特殊线段,那么在四边形中有这样特殊的线段吗,这节课我们将进行探究.二、师生互动,探求新知(一)梯形中位线概念问1:如图,在梯形ABCD中,M、N分别是腰AB与CD的中点,线段MN是梯形的什么线段?问2:能否类比三角形的中位线定义,给梯形的中位线下定义?问3:比较三角形中位线与梯形中位线的联系和区别.联系:都是联结两边中点的线段.区别:三角形中位线是联结任意两边中点,有三条;梯形中位线是联结两腰的中点,有且只有一条.(二)梯形中位线性质问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?师:下面我们来证明.已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.求证:MN//BC,MN=(AD+BC).分析:问:能否把MN转化为某个三角形的中位线,且该三角形的第三边恰好等于梯形两底之和?证明:联结AN并延长,交BC的延长线于点E.
∵AD//BC,
∴
∠1=∠E,∠D=∠2.
∵DN=NC,∴△ADN≌△ECN,
∴AN=EN,AD=EC.
∵AM=MB,
∴MN是△ABE的中位线.
∴MN//BC,MN=BE(三角形的中位线平行于第三边,并且等于第三边的一半).
∵BE=BC+CE=BC+AD,
∴MN=(BC+AD).因此,梯形的中位线具有以下性质:梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半.符号语言:∵MN是梯形ABCD的中位线,∴MN//
AD//BC,MN=(BC+AD)
(梯形的中位线平行于两底,并且等于两底和的一半).课堂练习:课本P100
第1题(口答)1.如图,梯形ABCD中,AD//BC,MN是它的中位线,(1)如果AD=3,BC=5,那么MN=
;(2)如果AD=5,MN=7,那么BC=
;(3)如果BC=a,MN=3,那么AD=
.【适时小结】1.“知二求一”:在梯形的上底、下底、中位线的三条线段中,已知其中两条线段的长度,就可求第三条线段的长度.2.梯形添加辅助线的方法:关于腰中点构造中心对称的全等三角形.三、定理运用例题7
一把梯子如图所示,其中四边形AKLB是梯形.已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m,CD=0.7
m,则EF=
、GH
=
、KL=
.分析:问1:在这个图形中,你发现了哪些梯形?为什么?问2:在哪个梯形中求EF、GH、KL的长?
答:
EF=0.8m,GH=0.9
m,KL=1m.例题8
已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.分析:问1:已知条件中有AD+BC,那么如何把它们加在一起?请学生简要说明过程.问2:由已知条件中的E为AB中点,及AD+BC联想到什么定理?
本题还有其它的证明方法吗?证明:取DC中点F,联结EF.
∵E为AB中点,∴EF为梯形的中位线,
∴EF//AD//BC,EF=(AD+BC)(梯形的中位线平行于两底,并且等于两底和的一半).
∴∠l=∠5.
∵DC=AD+BC,∴EF=DC=DF.∴∠1=∠2.
∴∠2=∠5,即DE平分∠ADC.同理,CE平分∠BCD.∵2(∠1+∠3)=180o,∴∠l+∠3=90o,∴DE⊥CE.【适时小结】梯形添加辅助线的方法:添梯形的中位线.四、课堂练习课本P100
第2、3题2.已知梯形的中位线长为m米,高为h米,那么梯形的面积是多少平方米?3.如图是一个形如直角梯形的鱼塘,已知AB=200m,BC=400m,CD=250m,E、F分别是AD、BC的中点.现要在E、F处建一道隔离栏,把鱼塘分给两家渔民进行承包,并且约定承包费用按照水面面积分摊,那么应按什么比例来分摊总承包金额?五、课堂小结谈谈这节课你有什么收获、体会或想法?教师补充:类比、化归、图形的分解组合的数学思想.六、布置作业几何本:堂堂练P76
10、11练习册:习题22.6(2)※分层作业在等腰梯形中,,,平分,、是对角线、的中点,且,求梯形的面积.
预设学生答1:联结三角形两边中点的线段叫做三角形的中位线.答2:三角形的中位线平行于第三边,并且等于第三边的一半.答1:梯形的中位线.答2:联结梯形两腰的中点的线段叫做梯形的中位线.答:(1)梯形的中位线平行于两底;(2)梯形的中位线长度等于两底和的一半.预设学生:(1)构造关于中点N的中心对称的全等三角形,(2)“截长补短”法.联结AN并延长,交BC的延长线于点E.(1)4;(2)9;(3)6?a.答1:梯形AKLB(已知),梯形AEFB和EKLF(由EF是梯形AKLB的中位线,得EF//AB//KL),梯形ABCD、CEFD、EGHF、GKLH、CGHD.答:在梯形AEFB中求EF;在梯形AKLB中求KL;在梯形EKLF中求GH.预设学生:通过“延长DE交CB的延长线于点F”来证明.答2:梯形中位线定理添梯形的中位线.S梯形=(a+b)·h
=mh(平方米)∵
E、F分别是AD、BC的中点,∴EF为梯形ABCD的中位线,∴EF=(AB+DC)=225S
AEFB=(AB+EF)·BFS
EDCF=(EF+DC)·FCBE=FC,∴S
AEFB:S
EDCF=(AB+EF):(EF+DC)=(200+225):(250+225)=17:19.预设学生:1.梯形中位线的概念.2.梯形中位线定理及运用.3.梯形添加辅助线的方法:(1)关于腰中点构造中心对称的全等三角形;(2)添梯形的中位线.
通过旧知识的回顾,找到新知识的突破点,有利于知识的正迁移.培养学生归纳概括的能力。突出概念中的“要素”—“两腰”,巩固新知并提高学生的识别能力.创设研究情境,引导学生通过观察、测量等猜测梯形中位线的性质;教师也可用几何画板呈现.引导学生把梯形中位线问题转化为三角形中位线的问题来解决,感受化归的数学思想.
通过练习巩固梯形中位线定理的运用,熟练上底、下底、中位线的三条线段之间的计算.利用数学与社会生活之间的联系,创设问题情境,激发学生求知欲.在复杂的图形中分解出不同的梯形,从而正确地找出梯形的中位线,感受图形的分解与组合的数学思学生可能会首先想到前面证明梯形中位线性质时用到的方法,关于腰中点构造中心对称的全等三角形.通过添加梯形的中位线,充分体现梯形中位线的桥梁作用.通过第2题的解答,可归纳梯形的又一面积公式:S梯形=中位线×高.第3题实际是求等高的两个梯形的面积之比.
梳理知识点,培养学生归纳反思的能力.
PAGE
5
三角形、梯形的中位线(2)
教学目标:
1.理解梯形的中位线概念,培养数学语言的表达和归纳能力.
2.在探索梯形中位线的性质过程,感受化归的数学思想.
3.掌握梯形中位线的性质定理,能运用定理进行计算和推理论证.
教学重点:梯形中位线性质定理的运用.
教学难点:梯形辅助线的添加.
教学过程:
教师活动
学生活动
教学设计意图
一、复习旧知,导入新课问1:什么叫三角形的中位线?问2:三角形的中位线有什么性质?三角形的中位线是三角形中的特殊线段,那么在四边形中有这样特殊的线段吗,这节课我们将进行探究.二、师生互动,探求新知(一)梯形中位线概念问1:如图,在梯形ABCD中,M、N分别是腰AB与CD的中点,线段MN是梯形的什么线段?问2:能否类比三角形的中位线定义,给梯形的中位线下定义?问3:比较三角形中位线与梯形中位线的联系和区别.联系:都是联结两边中点的线段.区别:三角形中位线是联结任意两边中点,有三条;梯形中位线是联结两腰的中点,有且只有一条.(二)梯形中位线性质问:类比三角形中位线的性质,梯形ABCD的中位线MN与两底之间存在怎样的数量与位置关系?师:下面我们来证明.已知:梯形ABCD中,AD//BC,AM=MB,DN=NC.求证:MN//BC,MN=(AD+BC).分析:问:能否把MN转化为某个三角形的中位线,且该三角形的第三边恰好等于梯形两底之和?证明:联结AN并延长,交BC的延长线于点E.
∵AD//BC,
∴
∠1=∠E,∠D=∠2.
∵DN=NC,∴△ADN≌△ECN,
∴AN=EN,AD=EC.
∵AM=MB,
∴MN是△ABE的中位线.
∴MN//BC,MN=BE(三角形的中位线平行于第三边,并且等于第三边的一半).
∵BE=BC+CE=BC+AD,
∴MN=(BC+AD).因此,梯形的中位线具有以下性质:梯形中位线定理
梯形的中位线平行于两底,并且等于两底和的一半.符号语言:∵MN是梯形ABCD的中位线,∴MN//
AD//BC,MN=(BC+AD)
(梯形的中位线平行于两底,并且等于两底和的一半).课堂练习:课本P100
第1题(口答)1.如图,梯形ABCD中,AD//BC,MN是它的中位线,(1)如果AD=3,BC=5,那么MN=
;(2)如果AD=5,MN=7,那么BC=
;(3)如果BC=a,MN=3,那么AD=
.【适时小结】1.“知二求一”:在梯形的上底、下底、中位线的三条线段中,已知其中两条线段的长度,就可求第三条线段的长度.2.梯形添加辅助线的方法:关于腰中点构造中心对称的全等三角形.三、定理运用例题7
一把梯子如图所示,其中四边形AKLB是梯形.已知AC=CE=EG=GK,BD=DF=FH=HL,AB=0.6m,CD=0.7
m,则EF=
、GH
=
、KL=
.分析:问1:在这个图形中,你发现了哪些梯形?为什么?问2:在哪个梯形中求EF、GH、KL的长?
答:
EF=0.8m,GH=0.9
m,KL=1m.例题8
已知:梯形ABCD中,AD//BC,E为AB中点,AD+BC=DC.求证:DE⊥EC,DE平分∠ADC,CE平分∠BCD.分析:问1:已知条件中有AD+BC,那么如何把它们加在一起?请学生简要说明过程.问2:由已知条件中的E为AB中点,及AD+BC联想到什么定理?
本题还有其它的证明方法吗?证明:取DC中点F,联结EF.
∵E为AB中点,∴EF为梯形的中位线,
∴EF//AD//BC,EF=(AD+BC)(梯形的中位线平行于两底,并且等于两底和的一半).
∴∠l=∠5.
∵DC=AD+BC,∴EF=DC=DF.∴∠1=∠2.
∴∠2=∠5,即DE平分∠ADC.同理,CE平分∠BCD.∵2(∠1+∠3)=180o,∴∠l+∠3=90o,∴DE⊥CE.【适时小结】梯形添加辅助线的方法:添梯形的中位线.四、课堂练习课本P100
第2、3题2.已知梯形的中位线长为m米,高为h米,那么梯形的面积是多少平方米?3.如图是一个形如直角梯形的鱼塘,已知AB=200m,BC=400m,CD=250m,E、F分别是AD、BC的中点.现要在E、F处建一道隔离栏,把鱼塘分给两家渔民进行承包,并且约定承包费用按照水面面积分摊,那么应按什么比例来分摊总承包金额?五、课堂小结谈谈这节课你有什么收获、体会或想法?教师补充:类比、化归、图形的分解组合的数学思想.六、布置作业几何本:堂堂练P76
10、11练习册:习题22.6(2)※分层作业在等腰梯形中,,,平分,、是对角线、的中点,且,求梯形的面积.
预设学生答1:联结三角形两边中点的线段叫做三角形的中位线.答2:三角形的中位线平行于第三边,并且等于第三边的一半.答1:梯形的中位线.答2:联结梯形两腰的中点的线段叫做梯形的中位线.答:(1)梯形的中位线平行于两底;(2)梯形的中位线长度等于两底和的一半.预设学生:(1)构造关于中点N的中心对称的全等三角形,(2)“截长补短”法.联结AN并延长,交BC的延长线于点E.(1)4;(2)9;(3)6?a.答1:梯形AKLB(已知),梯形AEFB和EKLF(由EF是梯形AKLB的中位线,得EF//AB//KL),梯形ABCD、CEFD、EGHF、GKLH、CGHD.答:在梯形AEFB中求EF;在梯形AKLB中求KL;在梯形EKLF中求GH.预设学生:通过“延长DE交CB的延长线于点F”来证明.答2:梯形中位线定理添梯形的中位线.S梯形=(a+b)·h
=mh(平方米)∵
E、F分别是AD、BC的中点,∴EF为梯形ABCD的中位线,∴EF=(AB+DC)=225S
AEFB=(AB+EF)·BFS
EDCF=(EF+DC)·FCBE=FC,∴S
AEFB:S
EDCF=(AB+EF):(EF+DC)=(200+225):(250+225)=17:19.预设学生:1.梯形中位线的概念.2.梯形中位线定理及运用.3.梯形添加辅助线的方法:(1)关于腰中点构造中心对称的全等三角形;(2)添梯形的中位线.
通过旧知识的回顾,找到新知识的突破点,有利于知识的正迁移.培养学生归纳概括的能力。突出概念中的“要素”—“两腰”,巩固新知并提高学生的识别能力.创设研究情境,引导学生通过观察、测量等猜测梯形中位线的性质;教师也可用几何画板呈现.引导学生把梯形中位线问题转化为三角形中位线的问题来解决,感受化归的数学思想.
通过练习巩固梯形中位线定理的运用,熟练上底、下底、中位线的三条线段之间的计算.利用数学与社会生活之间的联系,创设问题情境,激发学生求知欲.在复杂的图形中分解出不同的梯形,从而正确地找出梯形的中位线,感受图形的分解与组合的数学思学生可能会首先想到前面证明梯形中位线性质时用到的方法,关于腰中点构造中心对称的全等三角形.通过添加梯形的中位线,充分体现梯形中位线的桥梁作用.通过第2题的解答,可归纳梯形的又一面积公式:S梯形=中位线×高.第3题实际是求等高的两个梯形的面积之比.
梳理知识点,培养学生归纳反思的能力.
PAGE
5
