人教版八年级数学上册 《三角形全等》综合复习课件(共27张ppt)
文档属性
| 名称 | 人教版八年级数学上册 《三角形全等》综合复习课件(共27张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 07:52:13 | ||
图片预览






文档简介
(共27张PPT)
全等三角形综合复习
一、全等三角形:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
判定两个三角形全等的“四种思路”
找夹角(SAS);
1.已知两边
找直角(HL,SAS);
找另一边(SSS).
2.已知一边一角.
(1)边为角的对边时,找任一角(AAS).
找角的另一边(SAS);
(2)边为角的邻边时
找夹边的另一角(ASA);
找边的对角(AAS).
3.已知两角:找任意一边(AAS,ASA).
4.有直角,找两边(HL,SAS).
寻找对应元素的方法
1.全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.
2.全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.
3.有公共边的,公共边常是对应边.
4.有公共角的,公共角常是对应角.
5.有对顶角的,对顶角常是对应角.
6.两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).
应用全等三角形解题思路
1.利用全等三角形证明线段相等时,要找好背景三角形.
2.求证线段或角相等时考虑转化为证明它们所在的三角形全等.
3.当一个图形的某些条件变化后,要能分清变与不变的结果.
4.当遇到多边形问题时一般转化为三角形的问题解决.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.
三角形中常见辅助线的作法
1.延长中线构造全等三角形
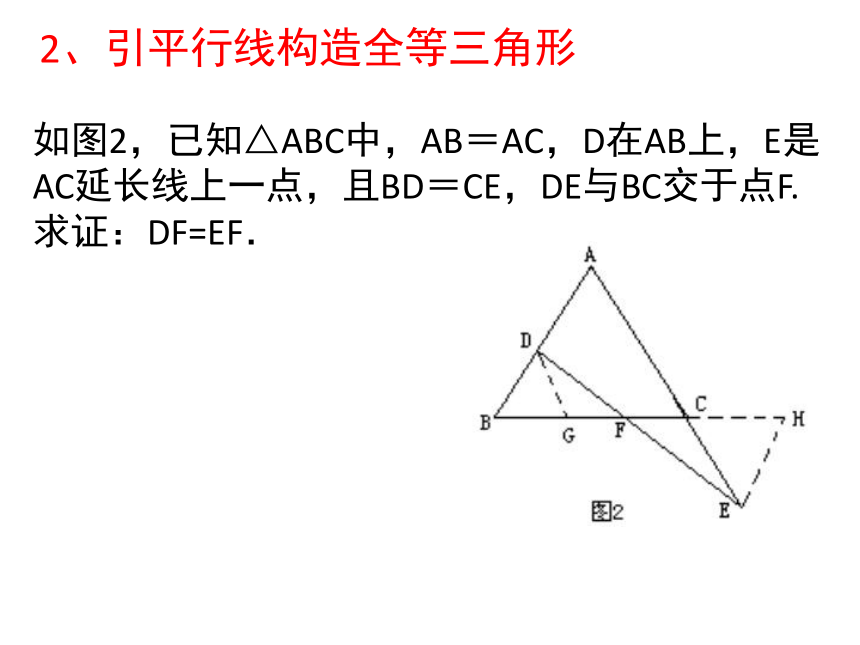
如图2,已知△ABC中,AB=AC,D在AB上,E是AC延长线上一点,且BD=CE,DE与BC交于点F.
求证:DF=EF.
2、引平行线构造全等三角形
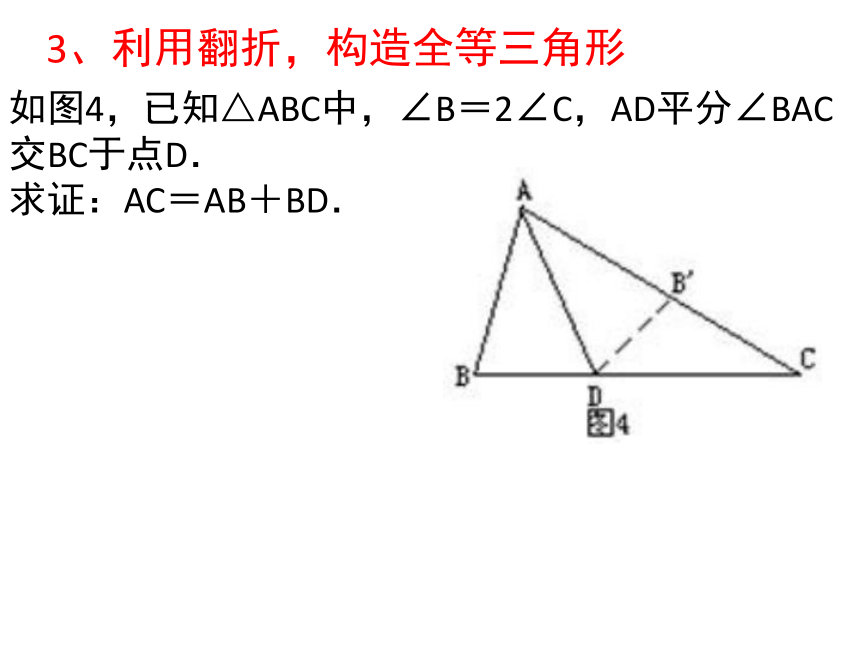
如图4,已知△ABC中,∠B=2∠C,AD平分∠BAC交BC于点D.
求证:AC=AB+BD.
3、利用翻折,构造全等三角形
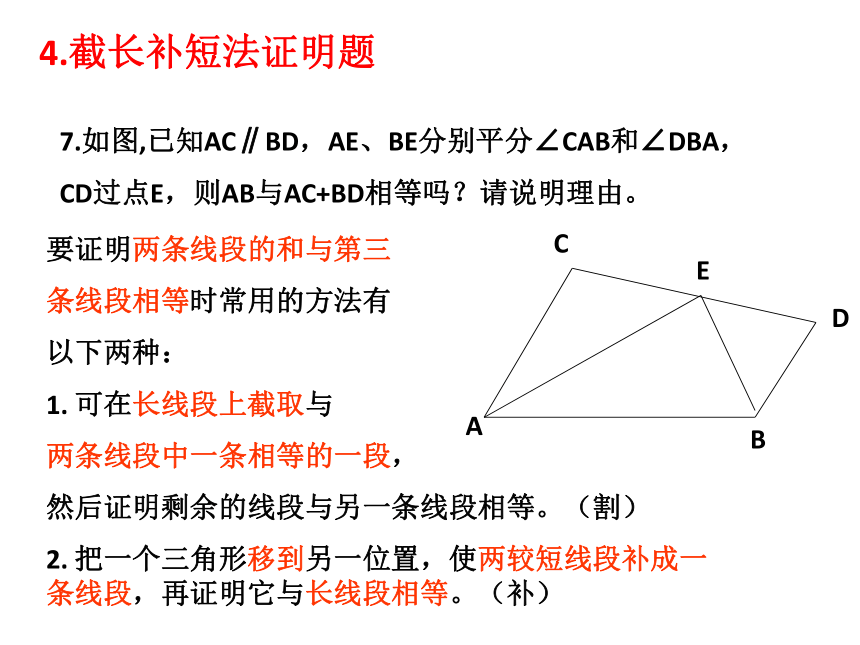
7.如图,已知AC∥BD,AE、BE分别平分∠CAB和∠DBA,
CD过点E,则AB与AC+BD相等吗?请说明理由。
A
C
E
B
D
要证明两条线段的和与第三
条线段相等时常用的方法有
以下两种:
1.
可在长线段上截取与
两条线段中一条相等的一段,
然后证明剩余的线段与另一条线段相等。(割)
2.
把一个三角形移到另一位置,使两较短线段补成一条线段,再证明它与长线段相等。(补)
4.截长补短法证明题
如图,把一个直角三角形ACB
(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG.
(2)求出∠FHG的度数.
如图,已知AD是△ABC的中线,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F.
求证:BE=CF.
如图:将纸片△ABC沿DE折叠,点A落在点F处,
已知∠1+∠2=100°,则∠A=
度;
努力就会有回报,
坚持就能够成功﹗
全等三角形综合复习
一、全等三角形:
1:什么是全等三角形?一个三角形经过哪些变化可以得到它的全等形?
2:全等三角形有哪些性质?
能够完全重合的两个三角形叫做全等三角形。一个三角形经过平移、翻折、旋转可以得到它的全等形。
(1)全等三角形的对应边相等、对应角相等。
(2)全等三角形的周长相等、面积相等。
(3)全等三角形的对应边上的对应中线、角平分线、高线分别相等。
判定两个三角形全等的“四种思路”
找夹角(SAS);
1.已知两边
找直角(HL,SAS);
找另一边(SSS).
2.已知一边一角.
(1)边为角的对边时,找任一角(AAS).
找角的另一边(SAS);
(2)边为角的邻边时
找夹边的另一角(ASA);
找边的对角(AAS).
3.已知两角:找任意一边(AAS,ASA).
4.有直角,找两边(HL,SAS).
寻找对应元素的方法
1.全等三角形对应角所对的边是对应边,两个对应角所夹的边是对应边.
2.全等三角形对应边所对的角是对应角,两条对应边所夹的角是对应角.
3.有公共边的,公共边常是对应边.
4.有公共角的,公共角常是对应角.
5.有对顶角的,对顶角常是对应角.
6.两个全等的不等边三角形中一对最长边(或最大角)是对应边(或对应角),一对最短边(或最小角)是对应边(或对应角).
应用全等三角形解题思路
1.利用全等三角形证明线段相等时,要找好背景三角形.
2.求证线段或角相等时考虑转化为证明它们所在的三角形全等.
3.当一个图形的某些条件变化后,要能分清变与不变的结果.
4.当遇到多边形问题时一般转化为三角形的问题解决.
如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE,DE,DC.
(1)求证:△ABE≌△CBD.
(2)若∠CAE=30°,求∠BDC的度数.
三角形中常见辅助线的作法
1.延长中线构造全等三角形
如图2,已知△ABC中,AB=AC,D在AB上,E是AC延长线上一点,且BD=CE,DE与BC交于点F.
求证:DF=EF.
2、引平行线构造全等三角形
如图4,已知△ABC中,∠B=2∠C,AD平分∠BAC交BC于点D.
求证:AC=AB+BD.
3、利用翻折,构造全等三角形
7.如图,已知AC∥BD,AE、BE分别平分∠CAB和∠DBA,
CD过点E,则AB与AC+BD相等吗?请说明理由。
A
C
E
B
D
要证明两条线段的和与第三
条线段相等时常用的方法有
以下两种:
1.
可在长线段上截取与
两条线段中一条相等的一段,
然后证明剩余的线段与另一条线段相等。(割)
2.
把一个三角形移到另一位置,使两较短线段补成一条线段,再证明它与长线段相等。(补)
4.截长补短法证明题
如图,把一个直角三角形ACB
(∠ACB=90°)绕着顶点B顺时针旋转60°,使得点C旋转到AB边上的一点D,点A旋转到点E的位置.F,G分别是BD,BE上的点,BF=BG,延长CF与DG交于点H.
(1)求证:CF=DG.
(2)求出∠FHG的度数.
如图,已知AD是△ABC的中线,分别过点B,C作BE⊥AD于点E,CF⊥AD交AD的延长线于点F.
求证:BE=CF.
如图:将纸片△ABC沿DE折叠,点A落在点F处,
已知∠1+∠2=100°,则∠A=
度;
努力就会有回报,
坚持就能够成功﹗
