北师大版六年级数学上期末复习第二讲圆的面积同步学案
文档属性
| 名称 | 北师大版六年级数学上期末复习第二讲圆的面积同步学案 |  | |
| 格式 | zip | ||
| 文件大小 | 353.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 20:46:57 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二讲
圆的面积
【考点解读1】圆的面积
圆的面积:圆的面积由半径或直径大小决定,通常用“S”表示。
知道直径:
知道半径:
知道周长:①先求出半径或直径;②再根据求出的直径或半径算出面积。
(4)常见的平方数:
=121
=144
=169
=196
=225
=256
=289
=324
=361
=400
圆的面积与半径的关系
半径扩大a倍,圆的面积扩大倍;
半径缩小a倍,圆的面积缩小倍。
圆的面积与直径的关系
直径扩大a倍,圆的面积扩大倍;
直径缩小a倍,圆的面积缩小倍。
【典例解析1】
如下图,把一个圆形纸片剪开后,拼成一个近似的长方形,这个长方形的周长是24.84厘米,圆形纸片的面积是__________平方厘米。(π取3.14)
分析:
【变式精讲1】
一个半圆形的花坛周长是30.84米,这个半圆形花坛的面积是(
)。
分析:
【考题演练1】
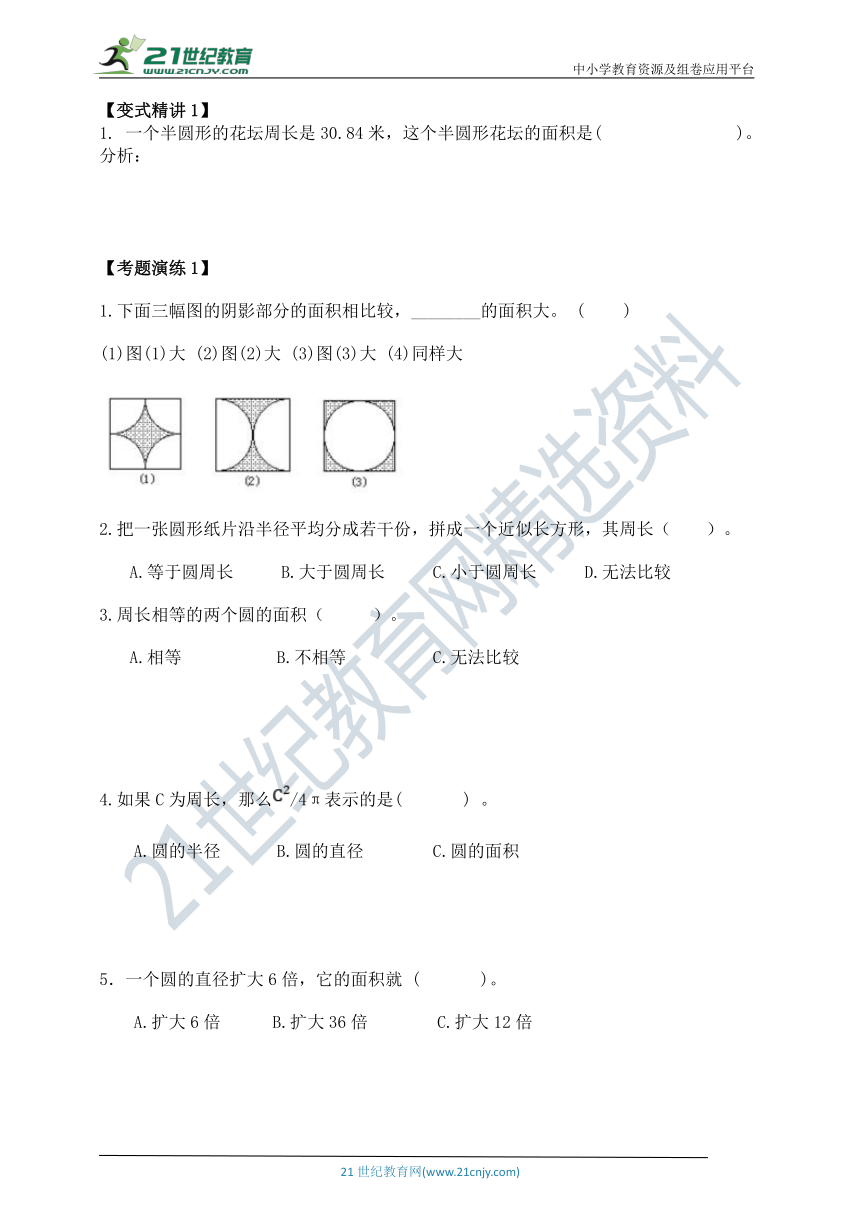
1.下面三幅图的阴影部分的面积相比较,________的面积大。
(
)
(1)图(1)大
(2)图(2)大
(3)图(3)大
(4)同样大
2.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长(
)。
A.等于圆周长
B.大于圆周长
C.小于圆周长
D.无法比较
3.周长相等的两个圆的面积(
)。
A.相等
B.不相等
C.无法比较
4.如果C为周长,那么/4π表示的是(
)
。
A.圆的半径
B.圆的直径
C.圆的面积
5.一个圆的直径扩大6倍,它的面积就
(
)。
A.扩大6倍
B.扩大36倍
C.扩大12倍
【考点解读2】阴影面积:圆与圆
圆环
(1)圆环的概念及组成要素:两个半径不等的圆,当圆心重合时,两圆之间的部分叫做圆环,下图阴影部分就是一个圆环。我们通常把较大的圆叫做外圆,半径用R表示;较小的圆叫内圆,用半径r表示。
(2)圆环的面积:圆环的面积等于外圆面积减去内圆面积。
圆与圆组成的复杂图形的阴影面积
仔细观察图中的圆的半径,以及半径之间的关系
仔细观察图形,将阴影部分转化成熟悉的图形
根据已知条件求解,注意解题过程和单位
对称轴
多个圆组成的复杂图形的对称轴一定至少经过一个圆的圆心
对称轴的性质依然满足
【典例解析2】
如下图,∠A=90度,阴影部分的面积是100平方厘米,求圆环的面积。
【变式精讲2】
1.甲乙两人分别绕下图的内圆(半径为30米)、外圆(半径为50米)跑步。
(1)两人各跑一圈相差多少米?(π≈3.14)
(2)求图中阴影部分的面积。(π≈3.14)
【考题演练2】
1.下图中大圆的直径是10厘米,四个小圆完全相同,求阴影部分的面积。
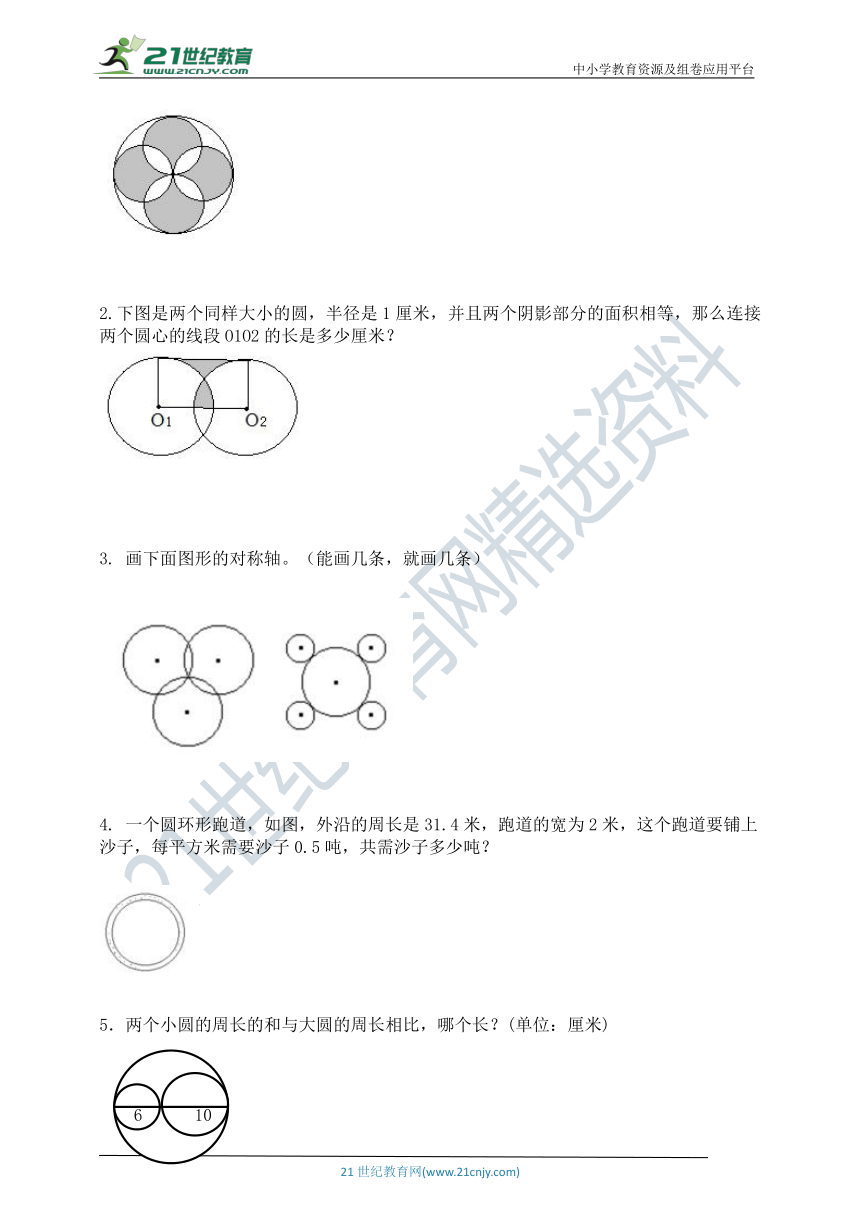
2.下图是两个同样大小的圆,半径是1厘米,并且两个阴影部分的面积相等,那么连接两个圆心的线段O1O2的长是多少厘米?
3.
画下面图形的对称轴。(能画几条,就画几条)
4.
一个圆环形跑道,如图,外沿的周长是31.4米,跑道的宽为2米,这个跑道要铺上沙子,每平方米需要沙子0.5吨,共需沙子多少吨?
5.两个小圆的周长的和与大圆的周长相比,哪个长?(单位:厘米)
6
10
【考点解读3】阴影面积:圆与三角形、梯形
解答圆与三角形、梯形组成的阴影面积此类题目时,需要注意
圆的直径、三角形的底和高或者是边长(梯形的上底、下底、高)必须弄清楚,以及它们之间的关系
根据题中已知的条件将阴影部分变形,转化为熟悉的图形求解
根据已知条件求解,注意解题过程和单位
【典例解析3】
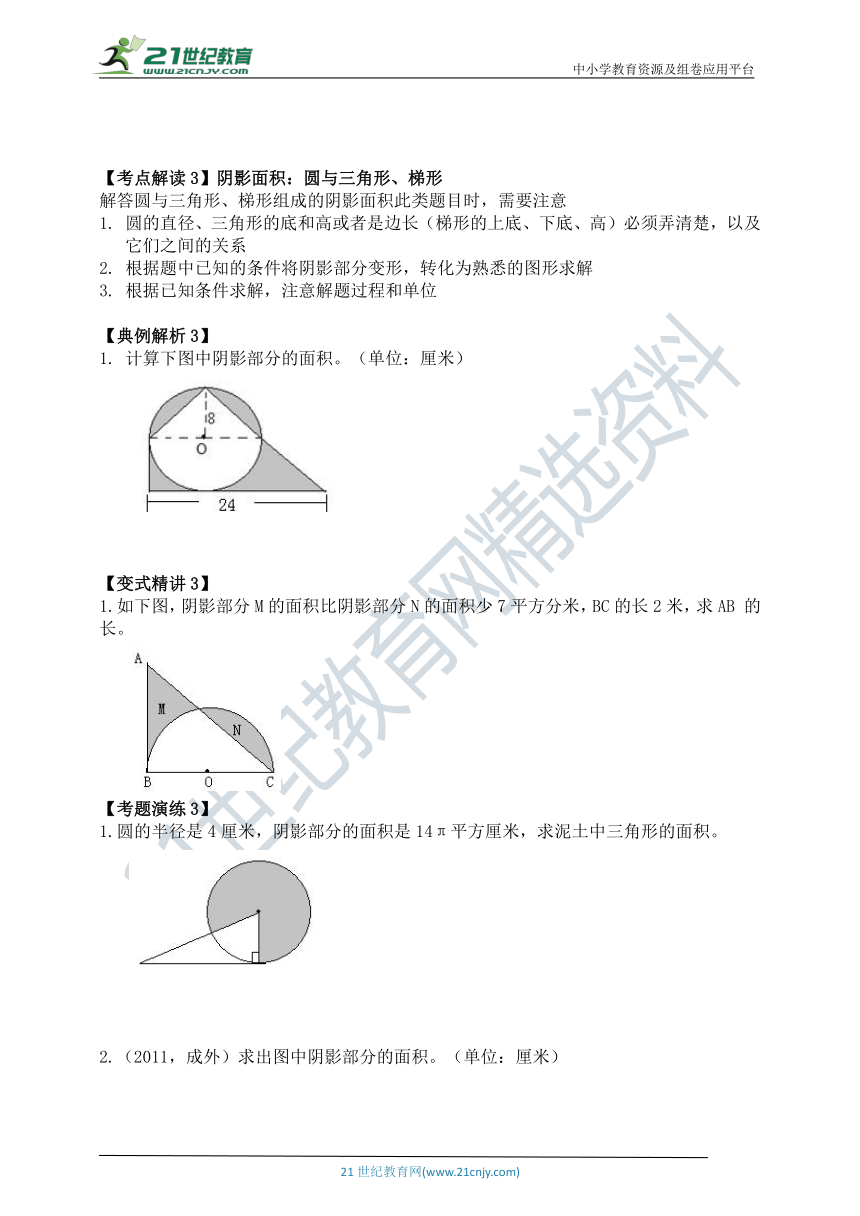
计算下图中阴影部分的面积。(单位:厘米)
【变式精讲3】
1.如下图,阴影部分M的面积比阴影部分N的面积少7平方分米,BC的长2米,求AB
的长。
【考题演练3】
1.圆的半径是4厘米,阴影部分的面积是14π平方厘米,求泥土中三角形的面积。
2.(2011,成外)求出图中阴影部分的面积。(单位:厘米)
【考点解读4】阴影面积:圆与正方形、长方形
解决此类题目时,应注意半径与边长的关系
1.
圆的直径、正方形的边长(长方形的长和宽),以及直径与它们的关系
2.根据题中已知的条件将阴影部分变形,转化为熟悉的图形求解
3.根据已知条件求解,注意解题过程和单位
【典例解析4】
如下图,一个圆与一个长方形重叠在一起,圆的面积与长方形的面积相等。已知圆的周长是6.28厘米,求阴影部分的周长。
【变式精讲4】
1.求下图中阴影部分的面积。(单位:分米)
【考题演练4】
已知圆的半径是1厘米,正方形的边长是10厘米,如果这个圆沿着正方形的里边滚一周再回到原处,那么
这个圆滚不到部分的面积是多少平方厘米?
这个圆的圆心所经过的路程长多少厘米?
2.求阴影部分的面积。(单位:厘米)
【考点解读5】圆与正方形、长方形
圆里最大的正方形
(1)圆里最大的正方形:正方形的对角线=直径。
正方形或长方形里最大的圆
(1)正方形里最大的圆:边长=直径。画法:①画出正方形的两条对角线;②以对角线交点为圆心,以边长为直径画圆。
(2)长方形里最大的圆:宽=直径。画法:①画出长方形的两条对角线;②以对角线交点为圆心,以宽为直径画圆。
【典例解析5】
1.在一块边长为4厘米的正方形的铁皮上,剪出直径为2厘米的小圆片,最多可剪(
)片。
A.3
B.4
C.5
D.6
分析:
【变式精讲5】
1.下图中两个正方形的面积之差是400平方厘米,那么两圆的面积之差是
(
)平方厘米。
分析:
【考题演练5】
1.一个圆的周长等于一个正方形的周长,那么这个圆的面积与正方形的面积比较,圆的面积(
)正方形的面积。
A.小于
B.大于
C.等于
D.约等于
分析:
2.同样周长的圆、正方形、长方形中,面积最大的是(
)。
A.圆
B.正方形
C.长方形
分析:
3.
在一个边长为4分米的正方形里,画一个最大的圆,这个圆的直径为(
)分米,半径为(
)分米,周长为(
)分米,面积为(
)平方分米。
分析:
4.如图,在推导圆的面积公式时,将圆分成了若干等份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,那么这个圆的面积是________平方厘米。(π取3.14)
第二讲
圆的面积
【典例解析1】
28.26
【变式精讲1】
113.04平方米
【考题演练1】
1.(4)
2.B
3.A
4.C
5.B
【典例解析2】
628平方厘米
【变式精讲2】
1.(1)125.6米
(2)5024平方米
【考题演练2】
1.50平方厘米
2.1.57cm
3.略
4.25.12吨
5.一样长,都等于16π
【典例解析3】
96平方厘米
【变式精讲3】
1.AB=1.5米
【考题演练3】
1.8平方厘米
2.11.25平方厘米
【典例解析4】
7.85厘米
【变式精讲4】
1.28.26平方分米
【考题演练4】
1.(1)36.86平方厘米
(2)32厘米
2.(1)25
(2)略
(3)24
(4)9
【典例解析5】
B
【变式精讲5】
1256
【考题演练5】
1.B
2.A
3.
4\2\12.56\12.56
4.28.26
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第二讲
圆的面积
【考点解读1】圆的面积
圆的面积:圆的面积由半径或直径大小决定,通常用“S”表示。
知道直径:
知道半径:
知道周长:①先求出半径或直径;②再根据求出的直径或半径算出面积。
(4)常见的平方数:
=121
=144
=169
=196
=225
=256
=289
=324
=361
=400
圆的面积与半径的关系
半径扩大a倍,圆的面积扩大倍;
半径缩小a倍,圆的面积缩小倍。
圆的面积与直径的关系
直径扩大a倍,圆的面积扩大倍;
直径缩小a倍,圆的面积缩小倍。
【典例解析1】
如下图,把一个圆形纸片剪开后,拼成一个近似的长方形,这个长方形的周长是24.84厘米,圆形纸片的面积是__________平方厘米。(π取3.14)
分析:
【变式精讲1】
一个半圆形的花坛周长是30.84米,这个半圆形花坛的面积是(
)。
分析:
【考题演练1】
1.下面三幅图的阴影部分的面积相比较,________的面积大。
(
)
(1)图(1)大
(2)图(2)大
(3)图(3)大
(4)同样大
2.把一张圆形纸片沿半径平均分成若干份,拼成一个近似长方形,其周长(
)。
A.等于圆周长
B.大于圆周长
C.小于圆周长
D.无法比较
3.周长相等的两个圆的面积(
)。
A.相等
B.不相等
C.无法比较
4.如果C为周长,那么/4π表示的是(
)
。
A.圆的半径
B.圆的直径
C.圆的面积
5.一个圆的直径扩大6倍,它的面积就
(
)。
A.扩大6倍
B.扩大36倍
C.扩大12倍
【考点解读2】阴影面积:圆与圆
圆环
(1)圆环的概念及组成要素:两个半径不等的圆,当圆心重合时,两圆之间的部分叫做圆环,下图阴影部分就是一个圆环。我们通常把较大的圆叫做外圆,半径用R表示;较小的圆叫内圆,用半径r表示。
(2)圆环的面积:圆环的面积等于外圆面积减去内圆面积。
圆与圆组成的复杂图形的阴影面积
仔细观察图中的圆的半径,以及半径之间的关系
仔细观察图形,将阴影部分转化成熟悉的图形
根据已知条件求解,注意解题过程和单位
对称轴
多个圆组成的复杂图形的对称轴一定至少经过一个圆的圆心
对称轴的性质依然满足
【典例解析2】
如下图,∠A=90度,阴影部分的面积是100平方厘米,求圆环的面积。
【变式精讲2】
1.甲乙两人分别绕下图的内圆(半径为30米)、外圆(半径为50米)跑步。
(1)两人各跑一圈相差多少米?(π≈3.14)
(2)求图中阴影部分的面积。(π≈3.14)
【考题演练2】
1.下图中大圆的直径是10厘米,四个小圆完全相同,求阴影部分的面积。
2.下图是两个同样大小的圆,半径是1厘米,并且两个阴影部分的面积相等,那么连接两个圆心的线段O1O2的长是多少厘米?
3.
画下面图形的对称轴。(能画几条,就画几条)
4.
一个圆环形跑道,如图,外沿的周长是31.4米,跑道的宽为2米,这个跑道要铺上沙子,每平方米需要沙子0.5吨,共需沙子多少吨?
5.两个小圆的周长的和与大圆的周长相比,哪个长?(单位:厘米)
6
10
【考点解读3】阴影面积:圆与三角形、梯形
解答圆与三角形、梯形组成的阴影面积此类题目时,需要注意
圆的直径、三角形的底和高或者是边长(梯形的上底、下底、高)必须弄清楚,以及它们之间的关系
根据题中已知的条件将阴影部分变形,转化为熟悉的图形求解
根据已知条件求解,注意解题过程和单位
【典例解析3】
计算下图中阴影部分的面积。(单位:厘米)
【变式精讲3】
1.如下图,阴影部分M的面积比阴影部分N的面积少7平方分米,BC的长2米,求AB
的长。
【考题演练3】
1.圆的半径是4厘米,阴影部分的面积是14π平方厘米,求泥土中三角形的面积。
2.(2011,成外)求出图中阴影部分的面积。(单位:厘米)
【考点解读4】阴影面积:圆与正方形、长方形
解决此类题目时,应注意半径与边长的关系
1.
圆的直径、正方形的边长(长方形的长和宽),以及直径与它们的关系
2.根据题中已知的条件将阴影部分变形,转化为熟悉的图形求解
3.根据已知条件求解,注意解题过程和单位
【典例解析4】
如下图,一个圆与一个长方形重叠在一起,圆的面积与长方形的面积相等。已知圆的周长是6.28厘米,求阴影部分的周长。
【变式精讲4】
1.求下图中阴影部分的面积。(单位:分米)
【考题演练4】
已知圆的半径是1厘米,正方形的边长是10厘米,如果这个圆沿着正方形的里边滚一周再回到原处,那么
这个圆滚不到部分的面积是多少平方厘米?
这个圆的圆心所经过的路程长多少厘米?
2.求阴影部分的面积。(单位:厘米)
【考点解读5】圆与正方形、长方形
圆里最大的正方形
(1)圆里最大的正方形:正方形的对角线=直径。
正方形或长方形里最大的圆
(1)正方形里最大的圆:边长=直径。画法:①画出正方形的两条对角线;②以对角线交点为圆心,以边长为直径画圆。
(2)长方形里最大的圆:宽=直径。画法:①画出长方形的两条对角线;②以对角线交点为圆心,以宽为直径画圆。
【典例解析5】
1.在一块边长为4厘米的正方形的铁皮上,剪出直径为2厘米的小圆片,最多可剪(
)片。
A.3
B.4
C.5
D.6
分析:
【变式精讲5】
1.下图中两个正方形的面积之差是400平方厘米,那么两圆的面积之差是
(
)平方厘米。
分析:
【考题演练5】
1.一个圆的周长等于一个正方形的周长,那么这个圆的面积与正方形的面积比较,圆的面积(
)正方形的面积。
A.小于
B.大于
C.等于
D.约等于
分析:
2.同样周长的圆、正方形、长方形中,面积最大的是(
)。
A.圆
B.正方形
C.长方形
分析:
3.
在一个边长为4分米的正方形里,画一个最大的圆,这个圆的直径为(
)分米,半径为(
)分米,周长为(
)分米,面积为(
)平方分米。
分析:
4.如图,在推导圆的面积公式时,将圆分成了若干等份,拼成一个近似的长方形,已知长方形的长比宽多6.42厘米,那么这个圆的面积是________平方厘米。(π取3.14)
第二讲
圆的面积
【典例解析1】
28.26
【变式精讲1】
113.04平方米
【考题演练1】
1.(4)
2.B
3.A
4.C
5.B
【典例解析2】
628平方厘米
【变式精讲2】
1.(1)125.6米
(2)5024平方米
【考题演练2】
1.50平方厘米
2.1.57cm
3.略
4.25.12吨
5.一样长,都等于16π
【典例解析3】
96平方厘米
【变式精讲3】
1.AB=1.5米
【考题演练3】
1.8平方厘米
2.11.25平方厘米
【典例解析4】
7.85厘米
【变式精讲4】
1.28.26平方分米
【考题演练4】
1.(1)36.86平方厘米
(2)32厘米
2.(1)25
(2)略
(3)24
(4)9
【典例解析5】
B
【变式精讲5】
1256
【考题演练5】
1.B
2.A
3.
4\2\12.56\12.56
4.28.26
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
