北师大版六年级数学上期末复习第四讲分数的混合运算(二)同步学案
文档属性
| 名称 | 北师大版六年级数学上期末复习第四讲分数的混合运算(二)同步学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 224.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
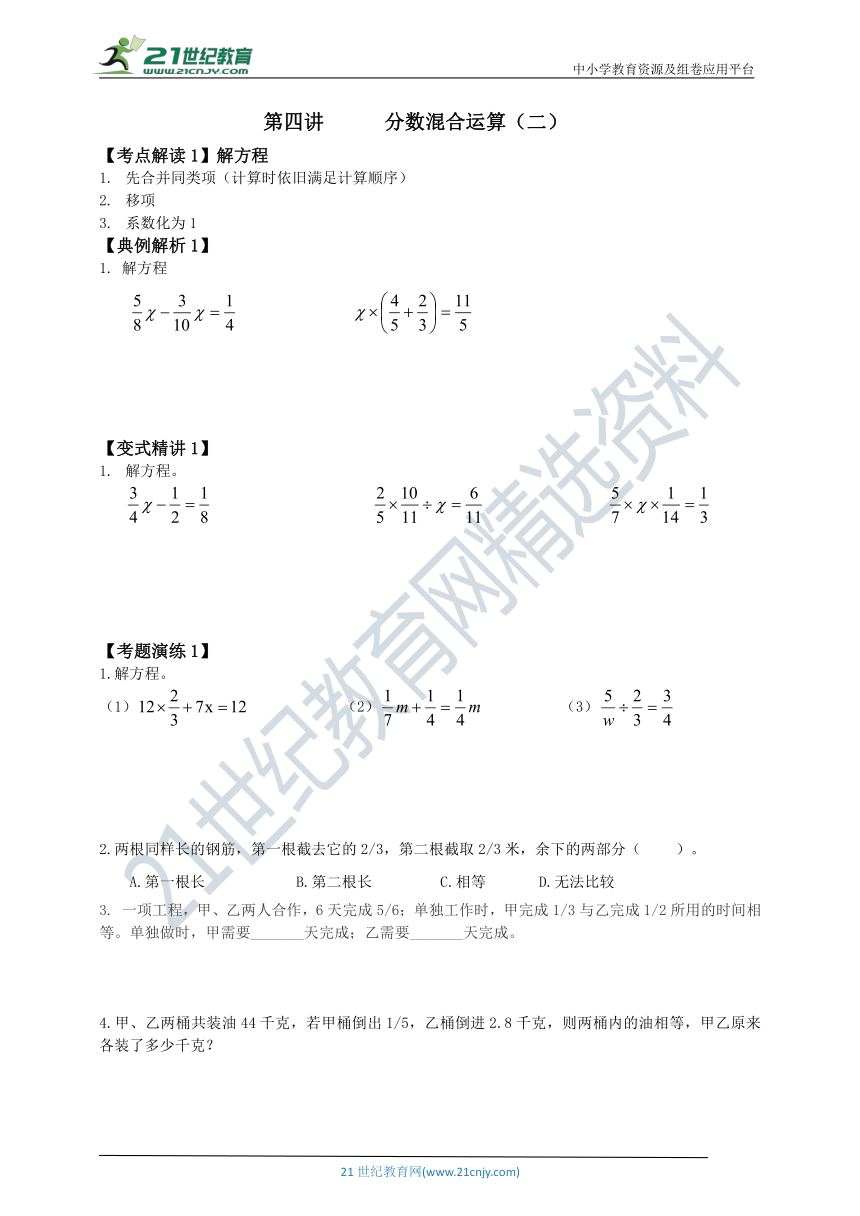
第四讲
分数混合运算(二)
【考点解读1】解方程
先合并同类项(计算时依旧满足计算顺序)
移项
系数化为1
【典例解析1】
1.
解方程
【变式精讲1】
解方程。
【考题演练1】
1.解方程。
(1)
(2)
(3)
2.两根同样长的钢筋,第一根截去它的2/3,第二根截取2/3米,余下的两部分(
)。
A.第一根长
B.第二根长
C.相等
D.无法比较
3.
一项工程,甲、乙两人合作,6天完成5/6;单独工作时,甲完成1/3与乙完成1/2所用的时间相等。单独做时,甲需要_______天完成;乙需要_______天完成。
4.甲、乙两桶共装油44千克,若甲桶倒出1/5,乙桶倒进2.8千克,则两桶内的油相等,甲乙原来各装了多少千克?
5.某工厂有若干工人,其中1/5是党员,n/3是团员(n是正整数),其余88人是群众,则此工厂共多少人?
【考点解读2】两个量之间的相互求解
两个量之间的相互求解:这种题型较简单,只涉及两个量(“单位1”和另一个量)及它们的关系,往往是知道一个量和它们之间的关系,求另一个量(比另一个多多少、少多少)
(1)求一个数的几分之几是多少:
(2)求比一个数多几分之几多多少:
(3)求比一个数多几分之几是多少:
(4)求比一个数少几分之几少多少:
(5)求比一个数少几分之几是多少:
【典例解析2】
(1)学校买来100千克白菜,吃了,吃了多少千克?
(2)小红体重42千克,小云体重40千克,小新体重相当于小红和小云体重总和的。小新体重是多少千克?
(3)小亮储蓄箱中有18元,小华储蓄的钱是小亮的,小新储蓄的钱是小华的。小新储蓄多少钱?
【变式精讲2】
有一摞纸,共120张。第一次用了它的,第二次用了它的,两次一共用了多少张纸?
【考题演练2】
1.国家一级保护动物野生丹顶鹤,2001年全世界约有2000只,我国占其中的,其它国家约有多少只?
人的心脏跳动的次数随着年龄而变化。青少年每分钟约跳75次,婴儿每分钟心跳的次数比青少年多。婴儿每分钟心跳比青少年多多少次?
3.学校有20个足球,篮球比足球多
,篮球有多少个?
4.学校有20个足球,篮球比足球少
,篮球比足球少多少个?
5.一种服装原价105元,现在降价,现在售价多少元?
【考点解读3】两个量求比率
两个量求比率:这类问题,往往是知道两个量(包括“单位1”和另一个量),要求两个量的关系(是几分之几、多几分之几、少几分之几),常见方法如下:
1.求一个数是另一个数的几分之几:
2.
求一个数比另一个数多几分之几:
3.
求一个数比另一个数少几分之几:
【典例解析3】
学校的果园里有梨树15棵,苹果树20棵。梨树的棵数是苹果树的几分之几?
【变式精讲3】
1.三年级有学生80人,二年级有学生60人,三年级学生比二年级学生多几分之几?
【考题演练3】
1.学校的果园里有梨树15棵,苹果树20棵。苹果树的棵数是梨树的几倍?
2.学校的果园里有梨树15棵,苹果树20棵。苹果树的棵数比梨树多几分之几?
3.学校的果园里有梨树15棵,苹果树20棵。梨树的棵数比苹果树少几分之几?
【考点解读4】两个量的逆向求解
解决这类题型,往往是知道另一个量和之间的关系,不知道“单位1”的量,求“单位1”,解决这类题型,一般使用逆向思维求解,一般使用除法。
已知一个数的几分之几是多少,求这个数是多少:
已知一个数比另一个数多几分之几多多少,求这个数多多少:
已知一个数比另一个数多几分之几是多少,求这个数是多少:
已知一个数比另一个数少几分之几少多少,求这个数少多少:
已知一个数比另一个数少几分之几是多少,求这个数是多少:
【典例解析4】
1.一条裤子的价格是75元,是一件上衣的。一件上衣多少元?
【变式精讲4】
1.水果店运一批水果。第一次运了50千克,第二次运了70千克,两次正好运了这批水果的。这批水果有多少千克?
【考题演练4】
1.(1)一个儿童体内所含水分有28千克,占体重的。这个儿童的体重有多少千克?
(2)一辆汽车从甲地开往乙地,第一小时行了全程的,第二小时行了全程的,两小时行了114千米。两地之间的公路长多少千米?
(3)小红家买来一袋大米,吃了,还剩15千克。买来大米多少千克?
(4)光明小学航模小组是生物小组的,生物小组的人数是美术小组的。航模小组有8人,美术小组有多少人?
(5)商店运来一些水果,运来苹果20筐,梨的筐数是苹果的,同时又是橘子的。运来橘子多少筐?
2.某工程队修筑一条公路。第一周修了这段公路的,第二周修筑了这段公路的,第二周比第一周多修了2千米。这段公路全长多少千米?
3.学校有20个足球,足球比篮球多
,篮球有多少个?
4.某工程队修筑一条公路。第一天修了38米,第二天了42米。第一天比第二天少修的是这条公路全长的。这条公路全长多少米?
5.学校有20个足球,足球比篮球少
,篮球有多少个?
【考点解读5】较复杂的分数应用题
这类题型,往往涉及两个“单位1”,这个时候需要仔细读题找准基本量,然后通过这三个量之间的两两对应关系解题,必要时候可以采用画关系图或者列小标题的形式解题。
【典例解析5】
1.学校食堂九月份用煤气640立方分米,十月份计划用煤气是九月份的,而十月份实际用煤气比原计划节约。十月份比原计划节约用煤气多少立方分米?
【变式精讲5】
1.(1)除以3与的差,商是多少?
(2)某数的比1.2的1倍多2.1,这个数是多少?
(3)已知慢车的速度是快车的,两车从甲乙两站同时相向而行在离中点4千米的地方相遇。求甲乙两站的距离是多少千米?
【考题演练5】
1.甲、乙、丙合做一批零件,甲做的是乙、丙的,乙做的是甲、丙的,丙做了25个,问这批零件有多少个?
2.一项工程,先由甲队独做2天,剩下的由甲、乙两队合作,3天可完成。如果单独完成这项工程,甲队所需天数是乙队所需天数的5/6,那么乙队单独完成这项工程需要多少天?
3.两列火车从甲、乙两地同时相对开出,4小时候在距中点48千米处相遇。已知慢车速度是快车速度的
,快车和慢车的速度各是多少?甲乙两地相距多少千米?
4.“六·一”那天,冬冬买了《昆虫王国的奥秘》和《海洋世界》两套丛书共用去260元,一套《昆虫王国的奥秘》丛书的价钱是《海洋世界》的,一套《海洋世界》丛书的价钱是多少元?
5.施工队有一批水泥,当用去这批水泥的30%后,又运来160袋,这时的水泥比原来的多
。那么,原来有水泥多少袋?
六年级普数(上)
第四讲(参考答案)
【典例解析1】
x=1
x=
【变式精讲1】
x=5/6
x=2/3
x=
【考题演练1】
1.x=4/7
m=
w=10
2.D
3.
甲=18天,乙=12天.
4.则甲桶中原来油重:46.8÷(1+4/5)=26(千克)乙桶中原来油重:44-26=18(千克)
5.共有660人
【典例解析2】
1.
100
×
=
80
(千克)
答:吃了80千克。
(2)(42
+40)×
=
41
(千克)答:小新体重41千克。
(3)
18
×
×=
10(元)答:小新储蓄10元。
【变式精讲2】
120×(+
)=92(张)
答:两次共用92张。
【考题演练2】
1.
2000×(1
—
)=
1500(只)答:其它国家约有1500只。
2.
75
×=
60(次)
答:婴儿每分钟心跳比青少年多跳60次。
3.
20×(1+
)=25(个)
答:篮球有25个。
4.
20×
=
4(个)答:篮球比足球少4个。
5.
105×(1
—
)=75(元)答:现在售价是75元。
【典例解析3】
1.
15÷20
=
答:梨树的棵数是苹果树的。
【变式精讲3】
1.1/3
【考题演练3】
1.
20÷15=
1
答:苹果树的棵数是梨树的1倍。
2.(20—15)÷15
=
答:苹果树的棵数比梨树多。
3.(20—15)÷20=
答:梨树的棵数比苹果树少。
【典例解析4】
1.
75÷=112(元)
答:一件上衣112元。
【变式精讲4】
1.(50+70)÷=480(千克)
答:
这批水果480千克。
【考题演练4】
1.(1)
28
÷
=
35(千克)
答:这个儿童体重35千克。
(2)114÷(+
)=216(千米)
答:两地之间的公路长216千米。
(3)15÷(1—
)=
40(千克)
答:
买来大米40千克。
(4)8÷÷=
30(人)
答:生物小组有30人。
(5)20×÷=
25(筐)
答:橘子有25
筐。
2.
2÷(
—
)=56(千米)
答:这段公路全长56千米。
3.
20÷(1+
)=16(个)
答:篮球有16个。
4.(42
—
38)÷=112(米)
答:这段公路全长112米。
5.
20÷(1—)=25(个)
答:篮球有25个。
【典例解析5】
1.
640××=144(立方分米)
答:十月份比原计划节约用煤气144立方分米。
【变式精讲5】
1.(1)12/35
(2)8.1
(3)88千米
【考题演练5】
60个
2.所以甲独做要:2+3+2.5=7.5(天)所以乙独做要:7.5÷5/6=9(天)
3.快车:
84(千米/时)慢车
=60(千米/时)路程:(84+60)×4=576(千米)
4.一套《海洋世界》丛书的价钱是160元
5.原来有400袋水泥
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
第四讲
分数混合运算(二)
【考点解读1】解方程
先合并同类项(计算时依旧满足计算顺序)
移项
系数化为1
【典例解析1】
1.
解方程
【变式精讲1】
解方程。
【考题演练1】
1.解方程。
(1)
(2)
(3)
2.两根同样长的钢筋,第一根截去它的2/3,第二根截取2/3米,余下的两部分(
)。
A.第一根长
B.第二根长
C.相等
D.无法比较
3.
一项工程,甲、乙两人合作,6天完成5/6;单独工作时,甲完成1/3与乙完成1/2所用的时间相等。单独做时,甲需要_______天完成;乙需要_______天完成。
4.甲、乙两桶共装油44千克,若甲桶倒出1/5,乙桶倒进2.8千克,则两桶内的油相等,甲乙原来各装了多少千克?
5.某工厂有若干工人,其中1/5是党员,n/3是团员(n是正整数),其余88人是群众,则此工厂共多少人?
【考点解读2】两个量之间的相互求解
两个量之间的相互求解:这种题型较简单,只涉及两个量(“单位1”和另一个量)及它们的关系,往往是知道一个量和它们之间的关系,求另一个量(比另一个多多少、少多少)
(1)求一个数的几分之几是多少:
(2)求比一个数多几分之几多多少:
(3)求比一个数多几分之几是多少:
(4)求比一个数少几分之几少多少:
(5)求比一个数少几分之几是多少:
【典例解析2】
(1)学校买来100千克白菜,吃了,吃了多少千克?
(2)小红体重42千克,小云体重40千克,小新体重相当于小红和小云体重总和的。小新体重是多少千克?
(3)小亮储蓄箱中有18元,小华储蓄的钱是小亮的,小新储蓄的钱是小华的。小新储蓄多少钱?
【变式精讲2】
有一摞纸,共120张。第一次用了它的,第二次用了它的,两次一共用了多少张纸?
【考题演练2】
1.国家一级保护动物野生丹顶鹤,2001年全世界约有2000只,我国占其中的,其它国家约有多少只?
人的心脏跳动的次数随着年龄而变化。青少年每分钟约跳75次,婴儿每分钟心跳的次数比青少年多。婴儿每分钟心跳比青少年多多少次?
3.学校有20个足球,篮球比足球多
,篮球有多少个?
4.学校有20个足球,篮球比足球少
,篮球比足球少多少个?
5.一种服装原价105元,现在降价,现在售价多少元?
【考点解读3】两个量求比率
两个量求比率:这类问题,往往是知道两个量(包括“单位1”和另一个量),要求两个量的关系(是几分之几、多几分之几、少几分之几),常见方法如下:
1.求一个数是另一个数的几分之几:
2.
求一个数比另一个数多几分之几:
3.
求一个数比另一个数少几分之几:
【典例解析3】
学校的果园里有梨树15棵,苹果树20棵。梨树的棵数是苹果树的几分之几?
【变式精讲3】
1.三年级有学生80人,二年级有学生60人,三年级学生比二年级学生多几分之几?
【考题演练3】
1.学校的果园里有梨树15棵,苹果树20棵。苹果树的棵数是梨树的几倍?
2.学校的果园里有梨树15棵,苹果树20棵。苹果树的棵数比梨树多几分之几?
3.学校的果园里有梨树15棵,苹果树20棵。梨树的棵数比苹果树少几分之几?
【考点解读4】两个量的逆向求解
解决这类题型,往往是知道另一个量和之间的关系,不知道“单位1”的量,求“单位1”,解决这类题型,一般使用逆向思维求解,一般使用除法。
已知一个数的几分之几是多少,求这个数是多少:
已知一个数比另一个数多几分之几多多少,求这个数多多少:
已知一个数比另一个数多几分之几是多少,求这个数是多少:
已知一个数比另一个数少几分之几少多少,求这个数少多少:
已知一个数比另一个数少几分之几是多少,求这个数是多少:
【典例解析4】
1.一条裤子的价格是75元,是一件上衣的。一件上衣多少元?
【变式精讲4】
1.水果店运一批水果。第一次运了50千克,第二次运了70千克,两次正好运了这批水果的。这批水果有多少千克?
【考题演练4】
1.(1)一个儿童体内所含水分有28千克,占体重的。这个儿童的体重有多少千克?
(2)一辆汽车从甲地开往乙地,第一小时行了全程的,第二小时行了全程的,两小时行了114千米。两地之间的公路长多少千米?
(3)小红家买来一袋大米,吃了,还剩15千克。买来大米多少千克?
(4)光明小学航模小组是生物小组的,生物小组的人数是美术小组的。航模小组有8人,美术小组有多少人?
(5)商店运来一些水果,运来苹果20筐,梨的筐数是苹果的,同时又是橘子的。运来橘子多少筐?
2.某工程队修筑一条公路。第一周修了这段公路的,第二周修筑了这段公路的,第二周比第一周多修了2千米。这段公路全长多少千米?
3.学校有20个足球,足球比篮球多
,篮球有多少个?
4.某工程队修筑一条公路。第一天修了38米,第二天了42米。第一天比第二天少修的是这条公路全长的。这条公路全长多少米?
5.学校有20个足球,足球比篮球少
,篮球有多少个?
【考点解读5】较复杂的分数应用题
这类题型,往往涉及两个“单位1”,这个时候需要仔细读题找准基本量,然后通过这三个量之间的两两对应关系解题,必要时候可以采用画关系图或者列小标题的形式解题。
【典例解析5】
1.学校食堂九月份用煤气640立方分米,十月份计划用煤气是九月份的,而十月份实际用煤气比原计划节约。十月份比原计划节约用煤气多少立方分米?
【变式精讲5】
1.(1)除以3与的差,商是多少?
(2)某数的比1.2的1倍多2.1,这个数是多少?
(3)已知慢车的速度是快车的,两车从甲乙两站同时相向而行在离中点4千米的地方相遇。求甲乙两站的距离是多少千米?
【考题演练5】
1.甲、乙、丙合做一批零件,甲做的是乙、丙的,乙做的是甲、丙的,丙做了25个,问这批零件有多少个?
2.一项工程,先由甲队独做2天,剩下的由甲、乙两队合作,3天可完成。如果单独完成这项工程,甲队所需天数是乙队所需天数的5/6,那么乙队单独完成这项工程需要多少天?
3.两列火车从甲、乙两地同时相对开出,4小时候在距中点48千米处相遇。已知慢车速度是快车速度的
,快车和慢车的速度各是多少?甲乙两地相距多少千米?
4.“六·一”那天,冬冬买了《昆虫王国的奥秘》和《海洋世界》两套丛书共用去260元,一套《昆虫王国的奥秘》丛书的价钱是《海洋世界》的,一套《海洋世界》丛书的价钱是多少元?
5.施工队有一批水泥,当用去这批水泥的30%后,又运来160袋,这时的水泥比原来的多
。那么,原来有水泥多少袋?
六年级普数(上)
第四讲(参考答案)
【典例解析1】
x=1
x=
【变式精讲1】
x=5/6
x=2/3
x=
【考题演练1】
1.x=4/7
m=
w=10
2.D
3.
甲=18天,乙=12天.
4.则甲桶中原来油重:46.8÷(1+4/5)=26(千克)乙桶中原来油重:44-26=18(千克)
5.共有660人
【典例解析2】
1.
100
×
=
80
(千克)
答:吃了80千克。
(2)(42
+40)×
=
41
(千克)答:小新体重41千克。
(3)
18
×
×=
10(元)答:小新储蓄10元。
【变式精讲2】
120×(+
)=92(张)
答:两次共用92张。
【考题演练2】
1.
2000×(1
—
)=
1500(只)答:其它国家约有1500只。
2.
75
×=
60(次)
答:婴儿每分钟心跳比青少年多跳60次。
3.
20×(1+
)=25(个)
答:篮球有25个。
4.
20×
=
4(个)答:篮球比足球少4个。
5.
105×(1
—
)=75(元)答:现在售价是75元。
【典例解析3】
1.
15÷20
=
答:梨树的棵数是苹果树的。
【变式精讲3】
1.1/3
【考题演练3】
1.
20÷15=
1
答:苹果树的棵数是梨树的1倍。
2.(20—15)÷15
=
答:苹果树的棵数比梨树多。
3.(20—15)÷20=
答:梨树的棵数比苹果树少。
【典例解析4】
1.
75÷=112(元)
答:一件上衣112元。
【变式精讲4】
1.(50+70)÷=480(千克)
答:
这批水果480千克。
【考题演练4】
1.(1)
28
÷
=
35(千克)
答:这个儿童体重35千克。
(2)114÷(+
)=216(千米)
答:两地之间的公路长216千米。
(3)15÷(1—
)=
40(千克)
答:
买来大米40千克。
(4)8÷÷=
30(人)
答:生物小组有30人。
(5)20×÷=
25(筐)
答:橘子有25
筐。
2.
2÷(
—
)=56(千米)
答:这段公路全长56千米。
3.
20÷(1+
)=16(个)
答:篮球有16个。
4.(42
—
38)÷=112(米)
答:这段公路全长112米。
5.
20÷(1—)=25(个)
答:篮球有25个。
【典例解析5】
1.
640××=144(立方分米)
答:十月份比原计划节约用煤气144立方分米。
【变式精讲5】
1.(1)12/35
(2)8.1
(3)88千米
【考题演练5】
60个
2.所以甲独做要:2+3+2.5=7.5(天)所以乙独做要:7.5÷5/6=9(天)
3.快车:
84(千米/时)慢车
=60(千米/时)路程:(84+60)×4=576(千米)
4.一套《海洋世界》丛书的价钱是160元
5.原来有400袋水泥
21世纪教育网
www.21cnjy.com
精品试卷·第
2
页
(共
2
页)
HYPERLINK
"http://21世纪教育网(www.21cnjy.com)
"
21世纪教育网(www.21cnjy.com)
同课章节目录
