安徽省蚌埠四中2020-2021学年第一学期12月月考word版含答案
文档属性
| 名称 | 安徽省蚌埠四中2020-2021学年第一学期12月月考word版含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 59.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览
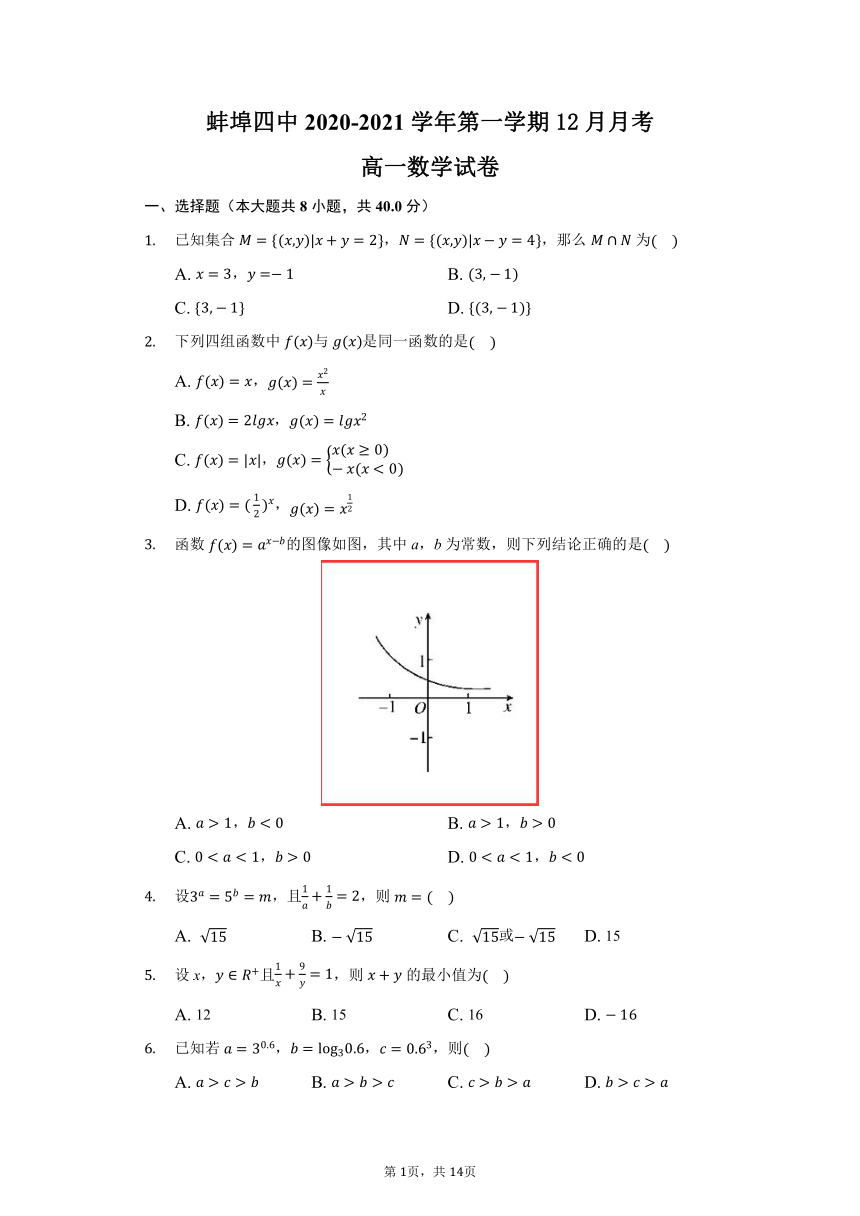




文档简介
蚌埠四中2020-2021学年第一学期12月月考
高一数学试卷
一、选择题(本大题共8小题,共40.0分)
已知集合,,那么为
A.
,
B.
C.
D.
下列四组函数中与是同一函数的是
A.
,
B.
,
C.
,
D.
,
函数的图像如图,其中a,b为常数,则下列结论正确的是
A.
,
B.
,
C.
,
D.
,
设,且,则
A.
B.
C.
或
D.
15
设x,且,则的最小值为
A.
12
B.
15
C.
16
D.
已知若,,,则
A.
B.
C.
D.
函数的单调递增区间是?
?
?
?
A.
B.
C.
D.
已知函数其中且的图象恒过定点A,若点A也在函数的图象上,则的值为?
?
?
A.
B.
C.
D.
二、不定项选择题((本大题共4小题,共20.0分。全部选对得5分,部分选对得3分,有选错的得0分))
在下面四个图中,可表示函数的图象的不可能是
A.
B.
C.
D.
设a,b,c为实数,且,则下列不等式中正确的是
A.
B.
C.
D.
下列结论中,正确的是
A.
B.
C.
若,则
D.
若,则
给定函数:,,,,其中在区间上单调递减的函数序号是???
A.
B.
C.
D.
三、填空题(本大题共4小题,共20.0分)
已知,,则的取值范围是______.
已知,则“”是“”的__________条件填:充分不必要、必要不充分、充要、既不充分又不必要
若,则x的值为________________.
已知函数的定义域是,则的定义域为____.
四、解答题(本大题共6小题,共72.0分)
已知全集,集合,.
当时,求集合;
若,求实数a的取值范围.
计算下列各式的值:
.
已知幂函数为偶函数.
求的解析式;
若在上不是单调函数,求实数a的取值范围.
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元设该公司的仪器月产量为x台,当月产量不超过400台时,总收益为元,当月产量超过400台时,总收益为80000元注:总收益总成本利润
将利润表示为月产量x的函数;
当月产量为何值时,公司所获利润最大?最大利润为多少元?
已知函数是定义在R上的奇函数,当时,.
求函数在R上的解析式;
用单调性定义证明函数在区间上是增函数.
设且,.
求a的值及的定义域;求在区间上的最大值.
答案和解析
1.【答案】D
【解析】
【分析】
此题考查了交集及其运算,以及二元一次方程组的解法,是一道基本题型,学生易弄错集合中元素的性质.
将集合M与集合N中的方程联立组成方程组,求出方程组的解即可确定出两集合的交集.
【解答】
解:将集合M和集合N中的方程联立得:
,
得:,
解得:,
得:,
解得:,
方程组的解为:,
则.
故选:D.
2.【答案】C
【解析】解:,,两个函数的定义域不相同,不是同一函数.
B.的定义域为,的定义域为,两个函数的定义域不相同,不是同一函数.
C.,两个函数定义域和对应法则相同,是同一函数.
D.两个函数的对应法则不相同,不是同一函数.
故选:C.
别判断两个函数的定义域和对应法则是否相同即可.
本题主要考查两个函数是否为同一函数,利用函数的定义域和对应法则是否相同是解决本题的关键,比较基础.
3.【答案】D
【解析】解:由图象得函数是减函数,
.
又分析得,图象是由的图象向左平移所得,
,即从而D正确.
故选D
根据函数的图象,确定函数的单调性,求出a的范围,结合指数函数的图象,推出b的范围,确定选项.
本题是基础题,考查学生视图能力,指数函数的图象变换,掌握指数函数的性质,才能正确解题.
4.【答案】A
【解析】解:设,且,
,,
,
解得.
故选:A.
推导出,,从而,由此能求出m.
本题考查实数值的求法,考查指数式、对数式的互化等基础知识,考查运算求解能力,是基础题.
5.【答案】C
【解析】
【分析】
利用基本不等式的性质即可得出.
熟练掌握基本不等式的性质是解题的关键.
【解答】
解:,,,,
当且仅当,即,时,取等号.
的最小值为16.
故选C.
6.【答案】A
【解析】解:若,
,
,
则,
故选:A.
根据指数函数以及对数函数的性质判断即可.
本题考查了指数函数以及对数函数的性质,是一道基础题.
7.【答案】D
【解析】
【分析】
本题主要考查复合函数的单调性及对数函数的图象和性质,属于基础题.
由得:或,令,结合复合函数单调性“同增异减”的原则,可得答案.
【解答】
解:由得:或,
即的定义域为或,
令,
在内单调递增,
而时,为减函数,时,为增函数,
故函数的单调递增区间是.
故选D.
8.【答案】A
【解析】
【分析】
本题考查了指数与指数幂的运算、对数与对数运算,属于基础题.
先利用函数的解析式得出其图象必过哪一个定点,再将该定点的坐标代入函数函数式中求出b,最后即可求出相应的函数值.
【解答】
解:函数的图象恒过定点,
将,代入得:,
,
,
则
.
故选A.
9.【答案】ABC
【解析】
【分析】
本题考查了函数的基本概念、函数的表示方法的相关知识,试题难度容易.
作一条与x轴垂直的直线,直线与函数图象至多有一个交点.
【解答】
解:根据函数的定义,任作一条与x轴垂直的直线,直线与函数图象至多有一个交点,
因此选项ABC不可能是函数图象.
故选ABC.
10.【答案】ACD
【解析】
【分析】
本题考查不等式的基本性质,考查指数函数、对数函数的单调性,熟练掌握不等式的基本性质,是解答的关键,属于基础题.
根据不等式的基本性质,结合已知,逐一分析四个答案中的不等式是否一定成立,可得答案.
【解答】
解:对于A,因为,所以,所以A正确;
对于B,当时,不成立,所以B错误;
对于C,因为,函数是R上的减函数,所以,所以C正确;
对于D,因为,所以,因为是上的增函数,所以,所以D正确.
故选ACD.
11.【答案】BD
【解析】
【分析】
本题考查对数的运算,属于基础题.
分别计算各个选项即可判断.
【解答】
解:,A错误
,B正确;
若,则,C错误.
若,则,D正确,
故选BD.
12.【答案】BC
【解析】
【试题解析】
【分析】
本题考查了函数的单调性,属于基础题.
根据函数的单调性对四个函数逐一分析,由此确定正确的命题序号.
【解答】
解:对于,函数在上递增,不符合题意.
对于,根据复合函数单调性同增异减可知,
函数在上递减,符合题意.
对于,当时,为减函数,符合题意.
对于,在上递增,不符合题意.
故选BC.
13.【答案】
【解析】
【分析】
本题考查不等式的性质,属于基础题根据不等式的性质求解即可.
【解答】
解:因为,,则,
所以,即的取值范围是.
故答案为?.
14.【答案】充分不必要
【解析】
【分析】
本题考查充要条件的判断,既要判断充分性,又要判断必要性,属基础题.
分别从充分性,必要性两个方面进行说明.
【解答】
解:由,
所以当时,,即充分性成立;
反之,若,得或,
故必要性不成立.
所以“”是“”的充分不必要条件.
故答案为:充分不必要.
15.【答案】100
【解析】
【分析】
本题考查指数方程和对数方程,是基础题.
由已知得,进一步可求出x的值.
【解答】
解:,
.
故答案为:100.
16.【答案】
【解析】
【分析】
本题考查抽象函数的定义域,属于简单题.
知的定义域求的定义域只要求的值域即可;知的定义域为,求的定义域只要解不等式的解集即可.
【解答】
解:定义域是,
,
的定义域是,
令,
解得,
故答案为:.
17.【答案】解:由得,即?????????????
由得,解得或,
即或??????????????????????????
Ⅰ当时,.
???????
Ⅱ或,
.
又,
,
解得.
实数a的取值范围是.
【解析】Ⅰ当时,求出集合A,利用集合的基本运算求.
Ⅱ求出,然后根据集合关系,确定a的取值范围.
本题主要考查集合的基本运算,以及利用集合关系确定参数问题,比较基础.
18.【答案】解:原式
原式
.
【解析】本题主要考查了指数与指数幂的运算,对数与对数的运算,属于基础题.
利用幂的运算性质计算即可得出结果;
利用对数的运算性质进行计算即可得出结果.
19.【答案】解:由题意,为幂函数,
所以,
解得:或3,
因为是偶函数,
所以,
所以;
,
的对称轴是,
若在上不是单调函数,
则,
解得:,
故实数a的取值范围是.
【解析】本题考查幂函数的解析式、函数的奇偶性,考查二次函数的性质,属于基础题.
根据幂函数的定义求出m的值,再根据函数为偶函数,即可求出函数的解析式;
若函数在上不是单调函数,可得,即可求出实数a的取值范围.
20.【答案】解:由题意得总成本为元,
所以利润.
当时,,
所以当时,的最大值为25000;
当时,是减函数,
所以,
综上,当月产量为300台时,公司所获利润最大,最大利润为25000元.
【解析】本题考查利用函数思想求解实际问题,求解函数的解析式是解题的关键,考查发现问题解决问题的能力,属于一般题.
利用已知条件,结合分段函数列出利润表示为月产量x的函数;
利用分段函数的解析式,分段求解函数的最大值即可.
21.【答案】解:设,则,
由时,可知,,
又为奇函数,故,
函数在R上的解析式为;
证明:设,则,
,
,
,即,
函数在区间上是增函数,得证.
【解析】利用奇函数的性质直接可以求得函数解析式,需要注意的是;
利用单调性定义直接证明即可.
本题考查利用函数奇偶性求函数解析式,考查函数单调性的证明,属于基础题.
22.【答案】解:,,
解得,
由,得,
函数的定义域为;
当时,是增函数;
当时,是减函数.
所以函数在上的最大值是.
【解析】本题考查了函数的定义域,函数的最值,对数函数的性质,属于中档题.
由即可求出a值,令可求出的定义域;
研究在区间上的单调性,由单调性可求出其最大值.
第6页,共14页
第5页,共14页
高一数学试卷
一、选择题(本大题共8小题,共40.0分)
已知集合,,那么为
A.
,
B.
C.
D.
下列四组函数中与是同一函数的是
A.
,
B.
,
C.
,
D.
,
函数的图像如图,其中a,b为常数,则下列结论正确的是
A.
,
B.
,
C.
,
D.
,
设,且,则
A.
B.
C.
或
D.
15
设x,且,则的最小值为
A.
12
B.
15
C.
16
D.
已知若,,,则
A.
B.
C.
D.
函数的单调递增区间是?
?
?
?
A.
B.
C.
D.
已知函数其中且的图象恒过定点A,若点A也在函数的图象上,则的值为?
?
?
A.
B.
C.
D.
二、不定项选择题((本大题共4小题,共20.0分。全部选对得5分,部分选对得3分,有选错的得0分))
在下面四个图中,可表示函数的图象的不可能是
A.
B.
C.
D.
设a,b,c为实数,且,则下列不等式中正确的是
A.
B.
C.
D.
下列结论中,正确的是
A.
B.
C.
若,则
D.
若,则
给定函数:,,,,其中在区间上单调递减的函数序号是???
A.
B.
C.
D.
三、填空题(本大题共4小题,共20.0分)
已知,,则的取值范围是______.
已知,则“”是“”的__________条件填:充分不必要、必要不充分、充要、既不充分又不必要
若,则x的值为________________.
已知函数的定义域是,则的定义域为____.
四、解答题(本大题共6小题,共72.0分)
已知全集,集合,.
当时,求集合;
若,求实数a的取值范围.
计算下列各式的值:
.
已知幂函数为偶函数.
求的解析式;
若在上不是单调函数,求实数a的取值范围.
某公司生产一种电子仪器的固定成本为20000元,每生产一台仪器需增加投入100元设该公司的仪器月产量为x台,当月产量不超过400台时,总收益为元,当月产量超过400台时,总收益为80000元注:总收益总成本利润
将利润表示为月产量x的函数;
当月产量为何值时,公司所获利润最大?最大利润为多少元?
已知函数是定义在R上的奇函数,当时,.
求函数在R上的解析式;
用单调性定义证明函数在区间上是增函数.
设且,.
求a的值及的定义域;求在区间上的最大值.
答案和解析
1.【答案】D
【解析】
【分析】
此题考查了交集及其运算,以及二元一次方程组的解法,是一道基本题型,学生易弄错集合中元素的性质.
将集合M与集合N中的方程联立组成方程组,求出方程组的解即可确定出两集合的交集.
【解答】
解:将集合M和集合N中的方程联立得:
,
得:,
解得:,
得:,
解得:,
方程组的解为:,
则.
故选:D.
2.【答案】C
【解析】解:,,两个函数的定义域不相同,不是同一函数.
B.的定义域为,的定义域为,两个函数的定义域不相同,不是同一函数.
C.,两个函数定义域和对应法则相同,是同一函数.
D.两个函数的对应法则不相同,不是同一函数.
故选:C.
别判断两个函数的定义域和对应法则是否相同即可.
本题主要考查两个函数是否为同一函数,利用函数的定义域和对应法则是否相同是解决本题的关键,比较基础.
3.【答案】D
【解析】解:由图象得函数是减函数,
.
又分析得,图象是由的图象向左平移所得,
,即从而D正确.
故选D
根据函数的图象,确定函数的单调性,求出a的范围,结合指数函数的图象,推出b的范围,确定选项.
本题是基础题,考查学生视图能力,指数函数的图象变换,掌握指数函数的性质,才能正确解题.
4.【答案】A
【解析】解:设,且,
,,
,
解得.
故选:A.
推导出,,从而,由此能求出m.
本题考查实数值的求法,考查指数式、对数式的互化等基础知识,考查运算求解能力,是基础题.
5.【答案】C
【解析】
【分析】
利用基本不等式的性质即可得出.
熟练掌握基本不等式的性质是解题的关键.
【解答】
解:,,,,
当且仅当,即,时,取等号.
的最小值为16.
故选C.
6.【答案】A
【解析】解:若,
,
,
则,
故选:A.
根据指数函数以及对数函数的性质判断即可.
本题考查了指数函数以及对数函数的性质,是一道基础题.
7.【答案】D
【解析】
【分析】
本题主要考查复合函数的单调性及对数函数的图象和性质,属于基础题.
由得:或,令,结合复合函数单调性“同增异减”的原则,可得答案.
【解答】
解:由得:或,
即的定义域为或,
令,
在内单调递增,
而时,为减函数,时,为增函数,
故函数的单调递增区间是.
故选D.
8.【答案】A
【解析】
【分析】
本题考查了指数与指数幂的运算、对数与对数运算,属于基础题.
先利用函数的解析式得出其图象必过哪一个定点,再将该定点的坐标代入函数函数式中求出b,最后即可求出相应的函数值.
【解答】
解:函数的图象恒过定点,
将,代入得:,
,
,
则
.
故选A.
9.【答案】ABC
【解析】
【分析】
本题考查了函数的基本概念、函数的表示方法的相关知识,试题难度容易.
作一条与x轴垂直的直线,直线与函数图象至多有一个交点.
【解答】
解:根据函数的定义,任作一条与x轴垂直的直线,直线与函数图象至多有一个交点,
因此选项ABC不可能是函数图象.
故选ABC.
10.【答案】ACD
【解析】
【分析】
本题考查不等式的基本性质,考查指数函数、对数函数的单调性,熟练掌握不等式的基本性质,是解答的关键,属于基础题.
根据不等式的基本性质,结合已知,逐一分析四个答案中的不等式是否一定成立,可得答案.
【解答】
解:对于A,因为,所以,所以A正确;
对于B,当时,不成立,所以B错误;
对于C,因为,函数是R上的减函数,所以,所以C正确;
对于D,因为,所以,因为是上的增函数,所以,所以D正确.
故选ACD.
11.【答案】BD
【解析】
【分析】
本题考查对数的运算,属于基础题.
分别计算各个选项即可判断.
【解答】
解:,A错误
,B正确;
若,则,C错误.
若,则,D正确,
故选BD.
12.【答案】BC
【解析】
【试题解析】
【分析】
本题考查了函数的单调性,属于基础题.
根据函数的单调性对四个函数逐一分析,由此确定正确的命题序号.
【解答】
解:对于,函数在上递增,不符合题意.
对于,根据复合函数单调性同增异减可知,
函数在上递减,符合题意.
对于,当时,为减函数,符合题意.
对于,在上递增,不符合题意.
故选BC.
13.【答案】
【解析】
【分析】
本题考查不等式的性质,属于基础题根据不等式的性质求解即可.
【解答】
解:因为,,则,
所以,即的取值范围是.
故答案为?.
14.【答案】充分不必要
【解析】
【分析】
本题考查充要条件的判断,既要判断充分性,又要判断必要性,属基础题.
分别从充分性,必要性两个方面进行说明.
【解答】
解:由,
所以当时,,即充分性成立;
反之,若,得或,
故必要性不成立.
所以“”是“”的充分不必要条件.
故答案为:充分不必要.
15.【答案】100
【解析】
【分析】
本题考查指数方程和对数方程,是基础题.
由已知得,进一步可求出x的值.
【解答】
解:,
.
故答案为:100.
16.【答案】
【解析】
【分析】
本题考查抽象函数的定义域,属于简单题.
知的定义域求的定义域只要求的值域即可;知的定义域为,求的定义域只要解不等式的解集即可.
【解答】
解:定义域是,
,
的定义域是,
令,
解得,
故答案为:.
17.【答案】解:由得,即?????????????
由得,解得或,
即或??????????????????????????
Ⅰ当时,.
???????
Ⅱ或,
.
又,
,
解得.
实数a的取值范围是.
【解析】Ⅰ当时,求出集合A,利用集合的基本运算求.
Ⅱ求出,然后根据集合关系,确定a的取值范围.
本题主要考查集合的基本运算,以及利用集合关系确定参数问题,比较基础.
18.【答案】解:原式
原式
.
【解析】本题主要考查了指数与指数幂的运算,对数与对数的运算,属于基础题.
利用幂的运算性质计算即可得出结果;
利用对数的运算性质进行计算即可得出结果.
19.【答案】解:由题意,为幂函数,
所以,
解得:或3,
因为是偶函数,
所以,
所以;
,
的对称轴是,
若在上不是单调函数,
则,
解得:,
故实数a的取值范围是.
【解析】本题考查幂函数的解析式、函数的奇偶性,考查二次函数的性质,属于基础题.
根据幂函数的定义求出m的值,再根据函数为偶函数,即可求出函数的解析式;
若函数在上不是单调函数,可得,即可求出实数a的取值范围.
20.【答案】解:由题意得总成本为元,
所以利润.
当时,,
所以当时,的最大值为25000;
当时,是减函数,
所以,
综上,当月产量为300台时,公司所获利润最大,最大利润为25000元.
【解析】本题考查利用函数思想求解实际问题,求解函数的解析式是解题的关键,考查发现问题解决问题的能力,属于一般题.
利用已知条件,结合分段函数列出利润表示为月产量x的函数;
利用分段函数的解析式,分段求解函数的最大值即可.
21.【答案】解:设,则,
由时,可知,,
又为奇函数,故,
函数在R上的解析式为;
证明:设,则,
,
,
,即,
函数在区间上是增函数,得证.
【解析】利用奇函数的性质直接可以求得函数解析式,需要注意的是;
利用单调性定义直接证明即可.
本题考查利用函数奇偶性求函数解析式,考查函数单调性的证明,属于基础题.
22.【答案】解:,,
解得,
由,得,
函数的定义域为;
当时,是增函数;
当时,是减函数.
所以函数在上的最大值是.
【解析】本题考查了函数的定义域,函数的最值,对数函数的性质,属于中档题.
由即可求出a值,令可求出的定义域;
研究在区间上的单调性,由单调性可求出其最大值.
第6页,共14页
第5页,共14页
