人教A版(2019)必修 第一册第五章 三角函数5.5三角恒等变换、三角函数的应用(课时训练)(word版含解析)
文档属性
| 名称 | 人教A版(2019)必修 第一册第五章 三角函数5.5三角恒等变换、三角函数的应用(课时训练)(word版含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 514.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-17 06:54:42 | ||
图片预览



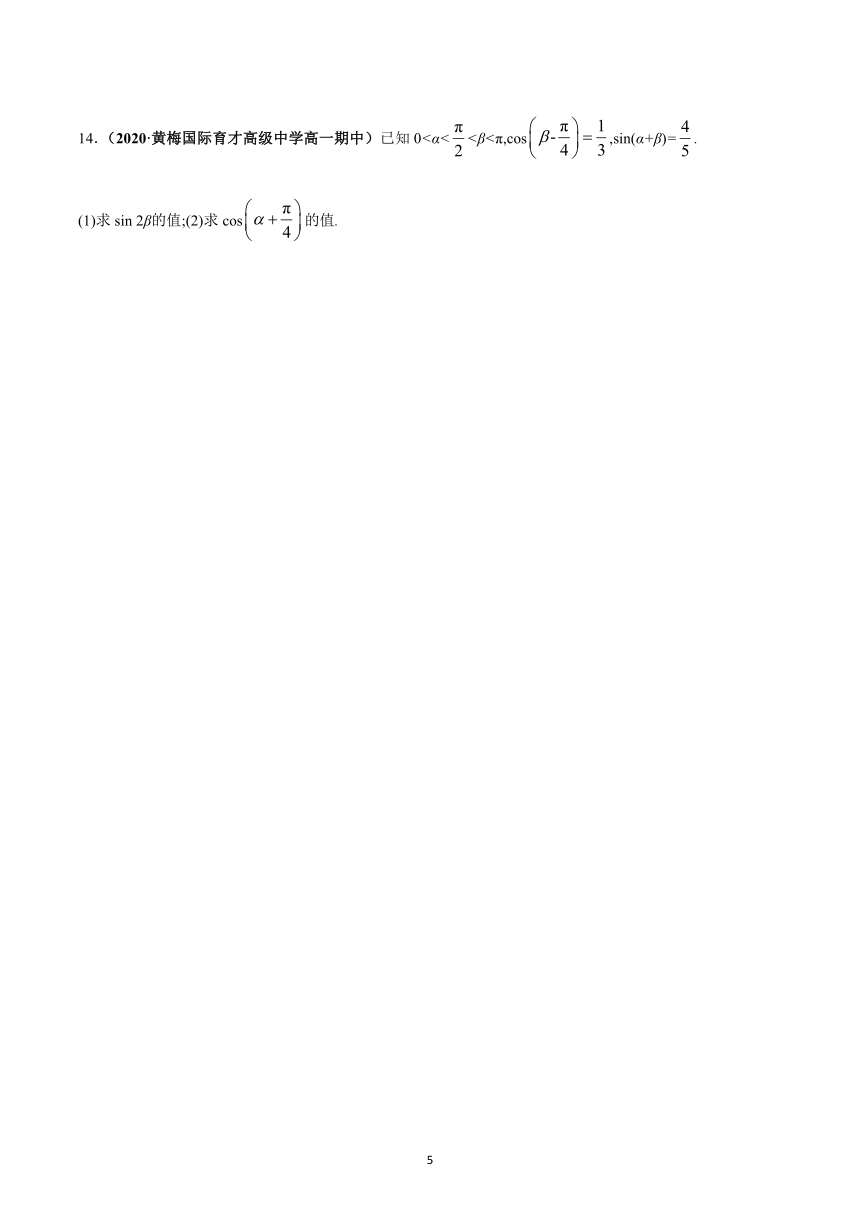
文档简介
专题14
三角恒等变换、三角函数的应用
【基础巩固】
1.(2020届四川省成都市高三第二次诊断)已知锐角满足则(
)
A.
B.
C.
D.
2.(2020届山西省大同市第一中学高三一模)已知,,则等于(
).
A.
B.
C.
D.
3.(2020·浙江高一课时练习)如图所示为一质点做简谐运动的图象,则下列判断中正确的是(
)
A.该质点的振动周期为
B.该质点的振幅为
C.该质点在和时振动速度最大
D.该质点在和时的振动速度为0
4.(2020届百校联考高考考前冲刺)已知为坐标原点,角的终边经过点且,则(
)
A.
B.
C.
D.
5.(2020届甘肃省兰州市高三诊断)已知函数(),若函数的图象与直线在上有3个不同的交点,则的取值范围是(
)
A.
B.
C.
D.
6.(2020·北京市平谷区高三一模)已知,那么______.
7.(2020届百校联考高考考前冲刺)若,则____.
8.已知函数f(x)=sin(2x)+1.
(1)用“五点法”作出f(x)在上的简图;
(2)写出f(x)的对称中心以及单调递增区间;
(3)求f(x)的最大值以及取得最大值时x的集合.
【能力提升】
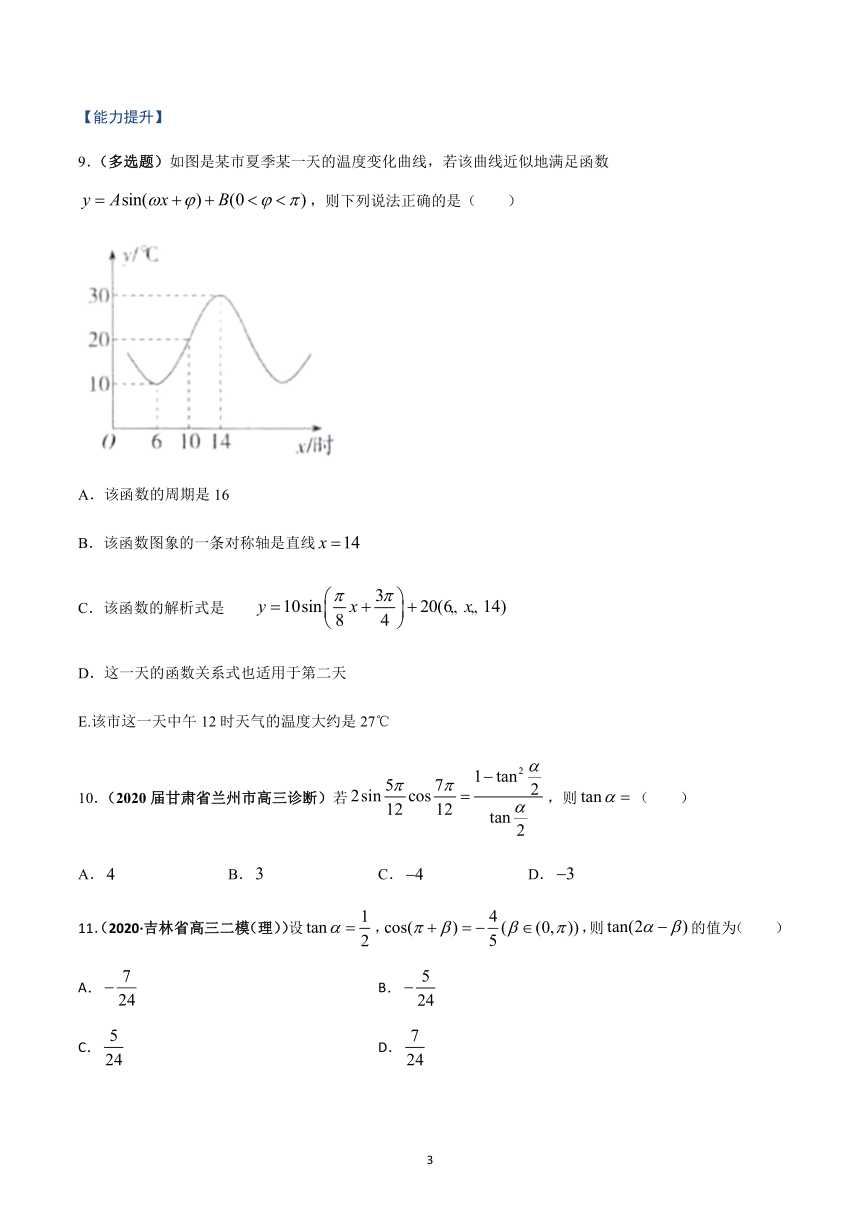
9.(多选题)如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是(
)
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
E.该市这一天中午12时天气的温度大约是27℃
10.(2020届甘肃省兰州市高三诊断)若,则(
)
A.
B.
C.
D.
11.(2020·吉林省高三二模(理))设,,则的值为(
)
A.
B.
C.
D.
12.(2020届安徽省“江南十校”高三综合素质检测)已知.给出下列判断:
①若,且,则;
②存在使得的图象向右平移个单位长度后得到的图象关于轴对称;
③若在上恰有7个零点,则的取值范围为;
④若在上单调递增,则的取值范围为.
其中,判断正确的个数为(
)
A.1
B.2
C.3
D.4
13.(2020·辉县市第二高级中学高一期中)已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h)
0
3
6
9
12
15
18
21
24
y(m)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
14.(2020·黄梅国际育才高级中学高一期中)已知0<α<<β<π,cos,sin(α+β)=.
(1)求sin
2β的值;(2)求cos的值.
15.已知函数.
(1)求的最小正周期;
(2)当时,求的值域.
专题14
三角恒等变换、三角函数的应用
【基础巩固】
1.(2020届四川省成都市高三第二次诊断)已知锐角满足则(
)
A.
B.
C.
D.
【答案】C
【解析】由已知,,因为锐角,所以,,
即,故选C。
2.(2020届山西省大同市第一中学高三一模)已知,,则等于(
).
A.
B.
C.
D.
【答案】B
【解析】由题意得
,又,所以,结合解得,所以
,故选B。
3.(2020·浙江高一课时练习)如图所示为一质点做简谐运动的图象,则下列判断中正确的是(
)
A.该质点的振动周期为
B.该质点的振幅为
C.该质点在和时振动速度最大
D.该质点在和时的振动速度为0
【答案】B
【解析】
由图象可知周期是,A错,振幅为,B正确;曲线上各点处的切线的斜率(导数值)才是相应的速度,质点在和时振动速度为0,C错,质点在和时的振动速度不为0,D错.
故选:B.
4.(2020届百校联考高考考前冲刺)已知为坐标原点,角的终边经过点且,则(
)
A.
B.
C.
D.
【答案】C
【解析】根据题意,,解得,
所以,
所以,
所以,故选C。
5.(2020届甘肃省兰州市高三诊断)已知函数(),若函数的图象与直线在上有3个不同的交点,则的取值范围是(
)
A.
B.
C.
D.
【答案】C
【解析】
,
的图象与直线在上有3个不同交点,
即方程在上有3个实根,
由得,所以,解得.
故选C。
6.(2020·北京市平谷区高三一模)已知,那么______.
【答案】
【解析】
∵,
∴,,
∴,故答案为。
7.(2020届百校联考高考考前冲刺)若,则____.
【答案】
【解析】因为,
所以,
所以.
8.(本小题满分12分)已知函数f(x)=sin(2x)+1.
(1)用“五点法”作出f(x)在上的简图;
(2)写出f(x)的对称中心以及单调递增区间;
(3)求f(x)的最大值以及取得最大值时x的集合.
【解析】(1)对于函数f(x)=sin(2x)+1,在上,2x∈[0,2π],列表:
2x
0
π
2
x
f(x)
1
2
1
0
1
作图:
(2)令2xkπ,求得x,可得函数的图象的对称中心为(,0),k∈Z.
令2kπ2x2kπ,求得kπx≤kπ,可得函数的增区间为[kπ,kπ],k∈Z.
(3
)令2x2kπ,求得x=kπ,可得函数f(x)的最大值为2,此时,x=kπ,k∈Z.[来
【能力提升】
9.(多选题)如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是(
)
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
E.该市这一天中午12时天气的温度大约是27℃
【答案】ABE
【解析】
由题意以及函数的图象可知,,,∴,.
∵,∴,A正确;∵,∴,
∴,∵图象经过点,
∴,∴,
∴可以取,∴,B正确,C错;这一天的函效关系式只适用于当天,第二天这个关系式不一定适用,∴D错;当时,,故E正确.综上,ABE正确.
故选:ABE
10.(2020届甘肃省兰州市高三诊断)若,则(
)
A.
B.
C.
D.
【答案】C
【解析】,
,由题意可得,因此,.
故选C。
11.(2020·吉林省高三二模(理))设,,则的值为(
)
A.
B.
C.
D.
【答案】D
【解析】,,,,
,,,。
12.(2020届安徽省“江南十校”高三综合素质检测)已知.给出下列判断:
①若,且,则;
②存在使得的图象向右平移个单位长度后得到的图象关于轴对称;
③若在上恰有7个零点,则的取值范围为;
④若在上单调递增,则的取值范围为.
其中,判断正确的个数为(
)
A.1
B.2
C.3
D.4
【答案】B
【解析】因为,所以周期.
对于①,因为,所以,即,故①错误;
对于②,函数的图象向右平移个单位长度后得到的函数为,其图象关于轴对称,则,解得,故对任意整数,,所以②错误;对于③,令,可得,则,
因为,所以在上第1个零点,且,所以第7个零点,若存在第8个零点,则,
所以,即,解得,故③正确;
对于④,因为,且,所以,解得,又,所以,故④正确,故选B。
13.(2020·辉县市第二高级中学高一期中)已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h)
0
3
6
9
12
15
18
21
24
y(m)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
【答案】(1)T=12,A=0.5,;(2)有6个小时可供冲浪者进行运动.
【解析】
试题分析:(1)由表中数据,知周期T=12,
.
由t=0,y=1.5,得A+b=1.5.
由t=3,y=1.0,得b=1.0.
∴A=0.5,b=1,
∴.
(2)由题意知,当y>1时才可对冲浪者开放.
∴>1,∴cost>0.
∴2kπ-t<2kπ+,
即12k-3∵0≤t≤24,故可令k分别为0、1、2,得0≤t<3或9∴在规定时间上午8:00至晚上20:00之间,有6个小时时间可供冲浪者运动,即上午9:00至下午15:00.
14.(2020·黄梅国际育才高级中学高一期中)已知0<α<<β<π,cos,sin(α+β)=.
(1)求sin
2β的值;(2)求cos的值.
【答案】(1);(2).
【解析】
(1)sin
2β=cos=cos
=2cos2-1=2×-1=.
(2)因为0<α<<β<π,所以<α+β<,所以sin>0,cos(α+β)<0,
又因为cos,sin(α+β)=,
所以sin,cos(α+β)=-,
所以cos=cos
=cos(α+β)cos+sin(α+β)sin=-.
15.已知函数.
(1)求的最小正周期;
(2)当时,求的值域.
【答案】(1);(2)
【解析】
(1)
,
,
即的最小正周期为;
(2),,
,
,
的值域为.
【高考真题】
三角恒等变换、三角函数的应用
【基础巩固】
1.(2020届四川省成都市高三第二次诊断)已知锐角满足则(
)
A.
B.
C.
D.
2.(2020届山西省大同市第一中学高三一模)已知,,则等于(
).
A.
B.
C.
D.
3.(2020·浙江高一课时练习)如图所示为一质点做简谐运动的图象,则下列判断中正确的是(
)
A.该质点的振动周期为
B.该质点的振幅为
C.该质点在和时振动速度最大
D.该质点在和时的振动速度为0
4.(2020届百校联考高考考前冲刺)已知为坐标原点,角的终边经过点且,则(
)
A.
B.
C.
D.
5.(2020届甘肃省兰州市高三诊断)已知函数(),若函数的图象与直线在上有3个不同的交点,则的取值范围是(
)
A.
B.
C.
D.
6.(2020·北京市平谷区高三一模)已知,那么______.
7.(2020届百校联考高考考前冲刺)若,则____.
8.已知函数f(x)=sin(2x)+1.
(1)用“五点法”作出f(x)在上的简图;
(2)写出f(x)的对称中心以及单调递增区间;
(3)求f(x)的最大值以及取得最大值时x的集合.
【能力提升】
9.(多选题)如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是(
)
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
E.该市这一天中午12时天气的温度大约是27℃
10.(2020届甘肃省兰州市高三诊断)若,则(
)
A.
B.
C.
D.
11.(2020·吉林省高三二模(理))设,,则的值为(
)
A.
B.
C.
D.
12.(2020届安徽省“江南十校”高三综合素质检测)已知.给出下列判断:
①若,且,则;
②存在使得的图象向右平移个单位长度后得到的图象关于轴对称;
③若在上恰有7个零点,则的取值范围为;
④若在上单调递增,则的取值范围为.
其中,判断正确的个数为(
)
A.1
B.2
C.3
D.4
13.(2020·辉县市第二高级中学高一期中)已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h)
0
3
6
9
12
15
18
21
24
y(m)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
14.(2020·黄梅国际育才高级中学高一期中)已知0<α<<β<π,cos,sin(α+β)=.
(1)求sin
2β的值;(2)求cos的值.
15.已知函数.
(1)求的最小正周期;
(2)当时,求的值域.
专题14
三角恒等变换、三角函数的应用
【基础巩固】
1.(2020届四川省成都市高三第二次诊断)已知锐角满足则(
)
A.
B.
C.
D.
【答案】C
【解析】由已知,,因为锐角,所以,,
即,故选C。
2.(2020届山西省大同市第一中学高三一模)已知,,则等于(
).
A.
B.
C.
D.
【答案】B
【解析】由题意得
,又,所以,结合解得,所以
,故选B。
3.(2020·浙江高一课时练习)如图所示为一质点做简谐运动的图象,则下列判断中正确的是(
)
A.该质点的振动周期为
B.该质点的振幅为
C.该质点在和时振动速度最大
D.该质点在和时的振动速度为0
【答案】B
【解析】
由图象可知周期是,A错,振幅为,B正确;曲线上各点处的切线的斜率(导数值)才是相应的速度,质点在和时振动速度为0,C错,质点在和时的振动速度不为0,D错.
故选:B.
4.(2020届百校联考高考考前冲刺)已知为坐标原点,角的终边经过点且,则(
)
A.
B.
C.
D.
【答案】C
【解析】根据题意,,解得,
所以,
所以,
所以,故选C。
5.(2020届甘肃省兰州市高三诊断)已知函数(),若函数的图象与直线在上有3个不同的交点,则的取值范围是(
)
A.
B.
C.
D.
【答案】C
【解析】
,
的图象与直线在上有3个不同交点,
即方程在上有3个实根,
由得,所以,解得.
故选C。
6.(2020·北京市平谷区高三一模)已知,那么______.
【答案】
【解析】
∵,
∴,,
∴,故答案为。
7.(2020届百校联考高考考前冲刺)若,则____.
【答案】
【解析】因为,
所以,
所以.
8.(本小题满分12分)已知函数f(x)=sin(2x)+1.
(1)用“五点法”作出f(x)在上的简图;
(2)写出f(x)的对称中心以及单调递增区间;
(3)求f(x)的最大值以及取得最大值时x的集合.
【解析】(1)对于函数f(x)=sin(2x)+1,在上,2x∈[0,2π],列表:
2x
0
π
2
x
f(x)
1
2
1
0
1
作图:
(2)令2xkπ,求得x,可得函数的图象的对称中心为(,0),k∈Z.
令2kπ2x2kπ,求得kπx≤kπ,可得函数的增区间为[kπ,kπ],k∈Z.
(3
)令2x2kπ,求得x=kπ,可得函数f(x)的最大值为2,此时,x=kπ,k∈Z.[来
【能力提升】
9.(多选题)如图是某市夏季某一天的温度变化曲线,若该曲线近似地满足函数,则下列说法正确的是(
)
A.该函数的周期是16
B.该函数图象的一条对称轴是直线
C.该函数的解析式是
D.这一天的函数关系式也适用于第二天
E.该市这一天中午12时天气的温度大约是27℃
【答案】ABE
【解析】
由题意以及函数的图象可知,,,∴,.
∵,∴,A正确;∵,∴,
∴,∵图象经过点,
∴,∴,
∴可以取,∴,B正确,C错;这一天的函效关系式只适用于当天,第二天这个关系式不一定适用,∴D错;当时,,故E正确.综上,ABE正确.
故选:ABE
10.(2020届甘肃省兰州市高三诊断)若,则(
)
A.
B.
C.
D.
【答案】C
【解析】,
,由题意可得,因此,.
故选C。
11.(2020·吉林省高三二模(理))设,,则的值为(
)
A.
B.
C.
D.
【答案】D
【解析】,,,,
,,,。
12.(2020届安徽省“江南十校”高三综合素质检测)已知.给出下列判断:
①若,且,则;
②存在使得的图象向右平移个单位长度后得到的图象关于轴对称;
③若在上恰有7个零点,则的取值范围为;
④若在上单调递增,则的取值范围为.
其中,判断正确的个数为(
)
A.1
B.2
C.3
D.4
【答案】B
【解析】因为,所以周期.
对于①,因为,所以,即,故①错误;
对于②,函数的图象向右平移个单位长度后得到的函数为,其图象关于轴对称,则,解得,故对任意整数,,所以②错误;对于③,令,可得,则,
因为,所以在上第1个零点,且,所以第7个零点,若存在第8个零点,则,
所以,即,解得,故③正确;
对于④,因为,且,所以,解得,又,所以,故④正确,故选B。
13.(2020·辉县市第二高级中学高一期中)已知某海滨浴场海浪的高度y(米)是时间t的(0≤t≤24,单位:小时)函数,记作y=f(t),下表是某日各时的浪高数据:
t(h)
0
3
6
9
12
15
18
21
24
y(m)
1.5
1.0
0.5
1.0
1.5
1.0
0.5
0.99
1.5
经长期观测,y=f(t)的曲线可近似地看成是函数y=Acosωt+b的图象.
(1)根据以上数据,求出函数y=Acosωt+b的最小正周期T、振幅A及函数表达式;
(2)依据规定,当海浪高度高于1米时才对冲浪爱好者开放,请依据(1)的结论,判断一天内的上午8时到晚上20时之间,有多长时间可供冲浪者进行运动?
【答案】(1)T=12,A=0.5,;(2)有6个小时可供冲浪者进行运动.
【解析】
试题分析:(1)由表中数据,知周期T=12,
.
由t=0,y=1.5,得A+b=1.5.
由t=3,y=1.0,得b=1.0.
∴A=0.5,b=1,
∴.
(2)由题意知,当y>1时才可对冲浪者开放.
∴>1,∴cost>0.
∴2kπ-
即12k-3
14.(2020·黄梅国际育才高级中学高一期中)已知0<α<<β<π,cos,sin(α+β)=.
(1)求sin
2β的值;(2)求cos的值.
【答案】(1);(2).
【解析】
(1)sin
2β=cos=cos
=2cos2-1=2×-1=.
(2)因为0<α<<β<π,所以<α+β<,所以sin>0,cos(α+β)<0,
又因为cos,sin(α+β)=,
所以sin,cos(α+β)=-,
所以cos=cos
=cos(α+β)cos+sin(α+β)sin=-.
15.已知函数.
(1)求的最小正周期;
(2)当时,求的值域.
【答案】(1);(2)
【解析】
(1)
,
,
即的最小正周期为;
(2),,
,
,
的值域为.
【高考真题】
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
