北师大版九年级下册数学 3.3垂径定理 同步练习(Word版 含解析)
文档属性
| 名称 | 北师大版九年级下册数学 3.3垂径定理 同步练习(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 358.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 23:26:44 | ||
图片预览




文档简介
3.3垂径定理 同步练习
一.选择题
1.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm B.4cm C.5cm D.6cm
2.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
3.如图,已知⊙O的半径为6,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.3 D.6
4.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )
A.13寸 B.26寸 C.18寸 D.24寸
5.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
6.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
7.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5 B. C.2 D.
8.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A. B.8 C. D.
9.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.4个 B.5个 C.6个 D.7个
10.如图,M是以AB为直径的半圆⊙O的内接四边形ABCD边CD的中点,MN⊥AB于点N,半圆的面积为π,AD=AN=3,则BC=( )
A.4 B.5 C.6 D.7
二.填空题
11.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
12.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
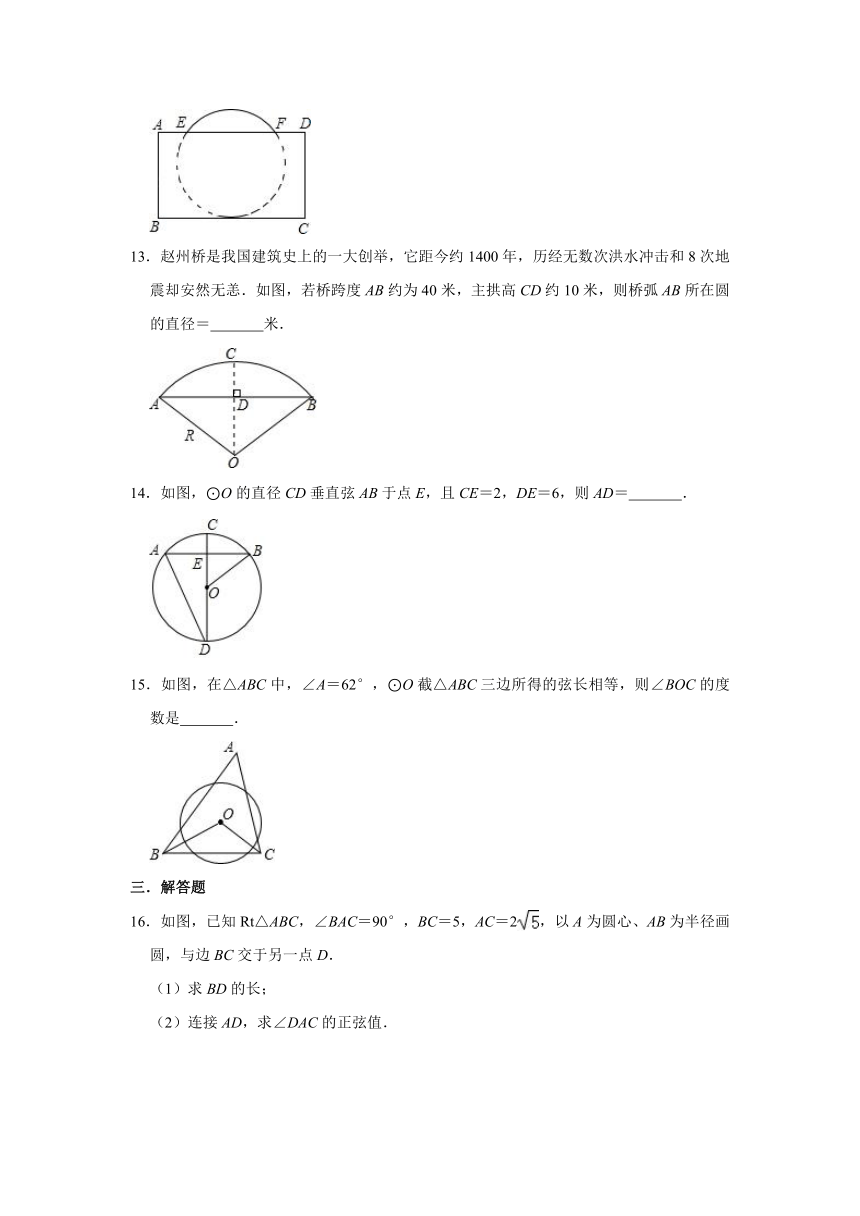
13.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径= 米.
14.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=6,则AD= .
15.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
三.解答题
16.如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
17.如图,已知⊙O的直径AB和弦CD相交于点E,AE=6cm,EB=2cm,∠BED=30°,求CD的长.
18.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=8,OG=10,求⊙O的半径.
参考答案
一.选择题
1.解:连接OA,如图:
∵AB=16cm,OC⊥AB,
∴AC=AB=8cm,
在Rt△OAC中,OC===6(cm),
故选:D.
2.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
3.解:作OE⊥AB于点E,
∵⊙O的半径为6,弦CD=6,
∴OC=OD=CD,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵∠AOB与∠COD互补,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵OA=6,OE⊥AB,
∴AE=OA?cos30°=6×=3,
∴AB=2AE=6,
故选:D.
4.解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r寸,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,
即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26寸.
故选:B.
5.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
6.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
8.解:连接BE,
∵AE为⊙O直径,
∴∠ABE=90°,
∵OD⊥AB,OD过O,
∴AC=BC=AB==4,
∵AO=OE,
∴BE=2OC,
∵OC=3,
∴BE=6,
在Rt△CBE中,EC===2,
故选:D.
9.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP===6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9.
根据对称性可知,满足条件的点P的个数有7个
故选:D.
10.解:作DE⊥AB于E,OF⊥AD于F,CP⊥AB于P,连接OC,如图所示:
则AF=DF=AD=,
∵MN⊥AB,
∴DE∥MN∥CP,
∵M是CD的中点,
∴EN=PN,
∵半圆的面积为π=π×OA2,
∴OA=5,
∵∠DEA=∠OFA=90°,∠DAE=∠OAF,
∴△ADE∽△AOF,
∴==,
∴AE=AF=×=,
∴PN=EN=AN﹣AE=3﹣=,
∴PA=AE+EN+PN=,
∴OP=PA﹣OA=,BP=OB﹣OP=,
∵CP⊥AB,
∴CP2=OC2﹣OP2=BC2﹣BP2,即52﹣()2=BC2﹣()2,
解得:BC=7;
故选:D.
二.填空题
11.解:连接BE,如图所示:
∵OD⊥AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,由勾股定理得:r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2,
故答案为:2.
12.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=12,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=12﹣x,MF=6,
在直角三角形OMF中,OM2+MF2=OF2
即:(12﹣x)2+62=x2
解得:x=7.5,
故答案为:7.5.
13.解:根据垂径定理,得AD=AB=20米.
设圆的半径是R,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米),
∴⊙O的直径为50米.
故答案为50.
14.解:
∵CE=2,DE=6,
∴CD=DE+CE=8,
∴OD=OB=OC=4,
∴OE=OC﹣CE=4﹣2=2,
在Rt△OEB中,由勾股定理得:BE===2,
∵CD⊥AB,CD过O,
∴AE=BE=2,
在Rt△AED中,由勾股定理得:AD===4,
故答案为:4.
15.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
三.解答题
16.解:(1)如图连接AD,作AH⊥BD于H.
∵Rt△ABC,∠BAC=90°,BC=5,AC=2,
∴AB==,
∵?AB?AC=?BC?AH,
∴AH==2,
∴BH==1,
∵AB=AD,AH⊥BD,
∴BH=HD=1,
∴BD=2.
(2)作DM⊥AC于M.
∵S△ACB=S△ABD+S△ACD,
∴××2=×2×2+×2×DM,
∴DM=,
∴sin∠DAC===.
17.解:过点O作OM⊥CD,连结OC,则CD=2CM,
∵AE=6cm,EB=2cm,
∴AB=8(cm),
∴OC=OB=4(cm),
∴OE=4﹣2=2(cm),
∵∠CEA=∠BED=30°,
∴OM=OE=×2=1(cm),
∴CM===(cm),
∴CD=2(cm).
18.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG.
(2)解:设⊙O的半径为r.则AG=OA+OG=r+10,
∵CA=CG,CD⊥AB,
∴AE=EG=,EC=ED=4,
∴OE=AE﹣OA=,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=()2+42,
解得r=或(舍弃),
∴⊙O的半径为.
一.选择题
1.如图所示,在半径为10cm的⊙O中,弦AB=16cm,OC⊥AB于点C,则OC等于( )
A.3cm B.4cm C.5cm D.6cm
2.往直径为52cm的圆柱形容器内装入一些水以后,截面如图所示,若水面宽AB=48cm,则水的最大深度为( )
A.8cm B.10cm C.16cm D.20cm
3.如图,已知⊙O的半径为6,弦AB,CD所对的圆心角分别是∠AOB,∠COD,若∠AOB与∠COD互补,弦CD=6,则弦AB的长为( )
A.6 B.8 C.3 D.6
4.《九章算术》总共收集了246个数学问题,这些算法要比欧洲同类算法早1500多年,对中国及世界数学发展产生过重要影响.在《九章算术》中有很多名题,下面就是其中的一道.原文:“今有圆材,埋在壁中,不知大小,以锯锯之,深一寸,锯道长一尺,问径几何?”翻译:如图,CD为⊙O的直径,弦AB⊥CD于点E.CE=1寸,AB=10寸,则可得直径CD的长为( )
A.13寸 B.26寸 C.18寸 D.24寸
5.如图,在⊙O中,弦AB=8,点C在AB上移动,连接OC,过点C作CD⊥OC交⊙O于点D,则CD的最大值是( )
A.2 B.4 C.6 D.8
6.如图所示,在⊙O中,AB为弦,OC⊥AB交AB于点D.且OD=DC.P为⊙O上任意一点,连接PA,PB,若⊙O的半径为1,则 S△PAB的最大值为( )
A.1 B. C. D.
7.如图,已知AB、AC都是⊙O的弦,OM⊥AB,ON⊥AC,垂足分别为M,N,若MN=,那么BC等于( )
A.5 B. C.2 D.
8.如图,⊙O的半径OD⊥弦AB于点C,连结AO并延长交⊙O于点E,连结EC.若AB=8,OC=3,则EC的长为( )
A. B.8 C. D.
9.如图,在⊙O中,半径r=10,弦AB=16,P是弦AB上的动点(不含端点A,B),若线段OP长为正整数,则点P的个数有( )
A.4个 B.5个 C.6个 D.7个
10.如图,M是以AB为直径的半圆⊙O的内接四边形ABCD边CD的中点,MN⊥AB于点N,半圆的面积为π,AD=AN=3,则BC=( )
A.4 B.5 C.6 D.7
二.填空题
11.如图,AB是⊙O的弦,半径OD⊥AB于点C,AE为直径,AB=8,CD=2,则线段CE的长为 .
12.把球放在长方体纸盒内,球的一部分露出盒外,其截面如图所示,已知EF=CD=12cm,则球的半径为 cm.
13.赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的直径= 米.
14.如图,⊙O的直径CD垂直弦AB于点E,且CE=2,DE=6,则AD= .
15.如图,在△ABC中,∠A=62°,⊙O截△ABC三边所得的弦长相等,则∠BOC的度数是 .
三.解答题
16.如图,已知Rt△ABC,∠BAC=90°,BC=5,AC=2,以A为圆心、AB为半径画圆,与边BC交于另一点D.
(1)求BD的长;
(2)连接AD,求∠DAC的正弦值.
17.如图,已知⊙O的直径AB和弦CD相交于点E,AE=6cm,EB=2cm,∠BED=30°,求CD的长.
18.如图,AB是⊙O直径,弦CD⊥AB于点E,过点C作DB的垂线,交AB的延长线于点G,垂足为点F,连结AC.
(1)求证:AC=CG;
(2)若CD=8,OG=10,求⊙O的半径.
参考答案
一.选择题
1.解:连接OA,如图:
∵AB=16cm,OC⊥AB,
∴AC=AB=8cm,
在Rt△OAC中,OC===6(cm),
故选:D.
2.解:连接OB,过点O作OC⊥AB于点D,交⊙O于点C,如图所示:
∵AB=48cm,
∴BD=AB=×48=24(cm),
∵⊙O的直径为52cm,
∴OB=OC=26cm,
在Rt△OBD中,OD===10(cm),
∴CD=OC﹣OD=26﹣10=16(cm),
故选:C.
3.解:作OE⊥AB于点E,
∵⊙O的半径为6,弦CD=6,
∴OC=OD=CD,
∴△DOC是等边三角形,
∴∠DOC=60°,
∵∠AOB与∠COD互补,
∴∠AOB=120°,
∵OA=OB,
∴∠OAB=∠OBA=30°,
∵OA=6,OE⊥AB,
∴AE=OA?cos30°=6×=3,
∴AB=2AE=6,
故选:D.
4.解:连接OA,AB⊥CD,
由垂径定理知,点E是AB的中点,AE=AB=5,OE=OC﹣CE=OA﹣CE,
设半径为r寸,由勾股定理得,OA2=AE2+OE2=AE2+(OA﹣CE)2,
即r2=52+(r﹣1)2,
解得:r=13,
所以CD=2r=26,
即圆的直径为26寸.
故选:B.
5.解:作OH⊥AB于H,连接OA、OD,如图,
∴AH=BH=AB=×8=4,
∵CD⊥OC,
∴CD=,
而OD为定值,OC最小时,CD最大,
∴当OC=OH时,CD的值最大,
∴CD的最大值为4.
故选:B.
6.解:连接OA,如图,
∵OC⊥AB,
∴AD=BD,
∵OD=DC,
∴OD=OA=,
∴AD==,AB=2AD=.
当点P为AB所对的优弧的中点时,△APB的面积最大,此时PD=PO+OD=1+=.
∴△APB的面积的最大值为===.
故选:C.
7.解:∵OM⊥AB,ON⊥AC,垂足分别为M、N,
∴M、N分别是AB与AC的中点,
∴MN是△ABC的中位线,
∴BC=2MN=2,
故选:C.
8.解:连接BE,
∵AE为⊙O直径,
∴∠ABE=90°,
∵OD⊥AB,OD过O,
∴AC=BC=AB==4,
∵AO=OE,
∴BE=2OC,
∵OC=3,
∴BE=6,
在Rt△CBE中,EC===2,
故选:D.
9.解:当P为AB的中点时,利用垂径定理得到OP⊥AB,此时OP最短,
∵AB=16,∴AP=BP=8,
在直角三角形AOP中,OA=10,AP=8,
根据勾股定理得:OP===6,即OP的最小值为6;
当P与A或B重合时,OP最长,此时OP=10,
∴6≤OP<10,
则使线段OP的长度为整数,
∴OP=6,7,8,9.
根据对称性可知,满足条件的点P的个数有7个
故选:D.
10.解:作DE⊥AB于E,OF⊥AD于F,CP⊥AB于P,连接OC,如图所示:
则AF=DF=AD=,
∵MN⊥AB,
∴DE∥MN∥CP,
∵M是CD的中点,
∴EN=PN,
∵半圆的面积为π=π×OA2,
∴OA=5,
∵∠DEA=∠OFA=90°,∠DAE=∠OAF,
∴△ADE∽△AOF,
∴==,
∴AE=AF=×=,
∴PN=EN=AN﹣AE=3﹣=,
∴PA=AE+EN+PN=,
∴OP=PA﹣OA=,BP=OB﹣OP=,
∵CP⊥AB,
∴CP2=OC2﹣OP2=BC2﹣BP2,即52﹣()2=BC2﹣()2,
解得:BC=7;
故选:D.
二.填空题
11.解:连接BE,如图所示:
∵OD⊥AB,AB=8,
∴AC=AB=4,
设⊙O的半径OA=r,
∴OC=OD﹣CD=r﹣2,
在Rt△OAC中,由勾股定理得:r2=(r﹣2)2+42,
解得:r=5,
∴AE=2r=10;
∵OD=5,CD=2,
∴OC=3,
∵AE是直径,
∴∠ABE=90°,
∵OC是△ABE的中位线,
∴BE=2OC=6,
在Rt△CBE中,CE===2,
故答案为:2.
12.解:EF的中点M,作MN⊥AD于点M,取MN上的球心O,连接OF,
∵四边形ABCD是矩形,
∴∠C=∠D=90°,
∴四边形CDMN是矩形,
∴MN=CD=12,
设OF=xcm,则ON=OF,
∴OM=MN﹣ON=12﹣x,MF=6,
在直角三角形OMF中,OM2+MF2=OF2
即:(12﹣x)2+62=x2
解得:x=7.5,
故答案为:7.5.
13.解:根据垂径定理,得AD=AB=20米.
设圆的半径是R,根据勾股定理,
得R2=202+(R﹣10)2,
解得R=25(米),
∴⊙O的直径为50米.
故答案为50.
14.解:
∵CE=2,DE=6,
∴CD=DE+CE=8,
∴OD=OB=OC=4,
∴OE=OC﹣CE=4﹣2=2,
在Rt△OEB中,由勾股定理得:BE===2,
∵CD⊥AB,CD过O,
∴AE=BE=2,
在Rt△AED中,由勾股定理得:AD===4,
故答案为:4.
15.解:∵△ABC中∠A=62°,⊙O截△ABC的三条边所得的弦长相等,
∴O到三角形三条边的距离相等,即O是△ABC的内心,
∴∠1=∠2,∠3=∠4,∠1+∠3=(180°﹣∠A)=(180°﹣62°)=59°,
∴∠BOC=180°﹣(∠1+∠3)=180°﹣59°=121°.
故答案是:121°.
三.解答题
16.解:(1)如图连接AD,作AH⊥BD于H.
∵Rt△ABC,∠BAC=90°,BC=5,AC=2,
∴AB==,
∵?AB?AC=?BC?AH,
∴AH==2,
∴BH==1,
∵AB=AD,AH⊥BD,
∴BH=HD=1,
∴BD=2.
(2)作DM⊥AC于M.
∵S△ACB=S△ABD+S△ACD,
∴××2=×2×2+×2×DM,
∴DM=,
∴sin∠DAC===.
17.解:过点O作OM⊥CD,连结OC,则CD=2CM,
∵AE=6cm,EB=2cm,
∴AB=8(cm),
∴OC=OB=4(cm),
∴OE=4﹣2=2(cm),
∵∠CEA=∠BED=30°,
∴OM=OE=×2=1(cm),
∴CM===(cm),
∴CD=2(cm).
18.(1)证明:∵DF⊥CG,CD⊥AB,
∴∠DEB=∠BFG=90°,
∵∠DBE=∠GBF,
∴∠D=∠G,
∵∠A=∠D,
∴∠A=∠G,
∴AC=CG.
(2)解:设⊙O的半径为r.则AG=OA+OG=r+10,
∵CA=CG,CD⊥AB,
∴AE=EG=,EC=ED=4,
∴OE=AE﹣OA=,
在Rt△OEC中,∵OC2=OE2+EC2,
∴r2=()2+42,
解得r=或(舍弃),
∴⊙O的半径为.
