北师大版七年级数学上学期《第4章 基本平面图形》单元练习 (word版 含解析)
文档属性
| 名称 | 北师大版七年级数学上学期《第4章 基本平面图形》单元练习 (word版 含解析) |  | |
| 格式 | zip | ||
| 文件大小 | 101.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 16:16:12 | ||
图片预览




文档简介
第4章
基本平面图形
一.选择题
1.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
2.下列说法不正确的有( )
①绝对值是本身的数是正数;
②符号不同的两个数互为相反数;
③两数相加,和一定大于任何一个加数;
④线段AB和线段BA表示的是同一条线段.
A.①③
B.②③
C.①②③
D.①②④
3.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
4.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③
B.③④
C.②③
D.②
5.如图1,A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小,图2中所示的C点即为所求的码头的位置,那么这样做的理由是( )
A.两直线相交只有一个交点
B.两点确定一条直线
C.两点之间,线段最短
D.经过一点有无数条直线
6.用两个钉子就可以把木条钉在墙上,其依据是( )
A.两点之间线段最短
B.两点之间直线最短
C.两点确定一条射线
D.两点确定一条直线
7.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
8.下列说法正确的是( )
A.两点之间直线最短
B.一个有理数,不是正数就是负数
C.平角是一条直线
D.整数和分数统称为有理数
9.下列语句中:正确的个数有( )
①画直线AB=3cm;
②连接点A与点B的线段,叫做A、B两点之间的距离;
③两条射线组成的图形叫角;
④任何一个有理数都可以用数轴上的一个点来表示.
A.0
B.1
C.2
D.3
10.钟表在3点30分时,它的时针和分针所成的角是( )
A.90°
B.75°
C.60°
D.45°
11.已知∠A=30°45',∠B=30.45°,则∠A( )∠B.(填“>”、“<”或“=”)
A.>
B.<
C.=
D.无法确定
12.如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角.若∠1=25°,那么∠AOB的度数是( )
A.65°
B.25°
C.90°
D.115°
13.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为( )
A.5
B.4
C.5或23
D.4或22
14.过六边形的一个顶点的对角线共有( )条.
A.1
B.2
C.3
D.4
15.已知⊙O中,最长的弦长为16cm,则⊙O的半径是( )
A.4cm
B.8cm
C.16cm
D.32cm
二.填空题
16.如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
17.平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条.
18.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为
.
19.已知点C,D在直线AB上,且AC=BD=1.5,若AB=7,则CD的长为
.
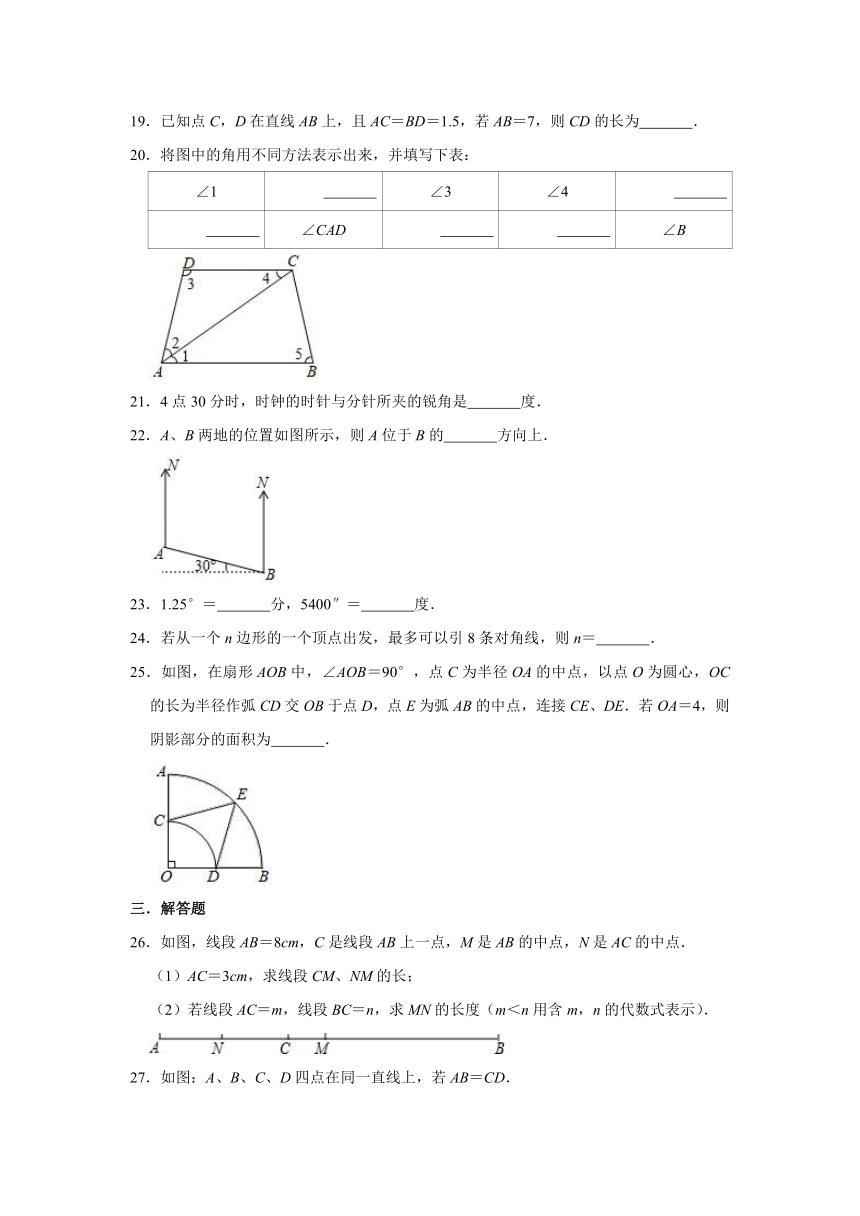
20.将图中的角用不同方法表示出来,并填写下表:
∠1
∠3
∠4
∠CAD
∠B
21.4点30分时,时钟的时针与分针所夹的锐角是
度.
22.A、B两地的位置如图所示,则A位于B的
方向上.
23.1.25°=
分,5400″=
度.
24.若从一个n边形的一个顶点出发,最多可以引8条对角线,则n=
.
25.如图,在扇形AOB中,∠AOB=90°,点C为半径OA的中点,以点O为圆心,OC的长为半径作弧CD交OB于点D,点E为弧AB的中点,连接CE、DE.若OA=4,则阴影部分的面积为
.
三.解答题
26.如图,线段AB=8cm,C是线段AB上一点,M是AB的中点,N是AC的中点.
(1)AC=3cm,求线段CM、NM的长;
(2)若线段AC=m,线段BC=n,求MN的长度(m<n用含m,n的代数式表示).
27.如图:A、B、C、D四点在同一直线上,若AB=CD.
①图中共有
条线段;
②比较线段的大小:AC
BD(填“>”、“=”或“<”);
③若BC=AC,且AC=6cm,则AD的长为
cm;
28.(1)如图①,过角的顶点在角的内部作一条射线,那么图中一共有多少个角?
(2)如图②,过角的顶点在角的内部作两条射线,那么图中一共有多少个角?
(3)如图③,过角的顶点在角的内部作n条射线,那么图中一共有多少个角?
29.如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
30.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD,求∠BOD的度数.
参考答案
一.选择题
1.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
2.解:①绝对值是本身的数是非负数,故①符合题意;
②符号不同的两个数不一定是互为相反数,故②符合题意;
③两数相加,和不一定大于任何一个加数,故③符合题意;
④线段AB和线段BA表示的是同一条线段,故④不符合题意,
故选:C.
3.解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
4.解:①通过测量发现车站的位置设在C点好于B点,故原来的结论正确;
②车站设在B点与C点之间公路上,车站朝M方向始终有4个工厂,车站朝N方向始终有3个工厂,所以在这一段任何一点,效果一样,故原来的结论错误;
③工厂到车站的距离是线段的长,和各段的弯曲的小公路无关,故原来的结论正确;
④车站的位置设在BC段公路的最中间处与设在点B及点C处一样好,故原来的结论错误.
故选:A.
5.解:A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小,图2中所示的C点即为所求的码头的位置,那么这样做的理由是两点之间,线段最短,
故选:C.
6.解:用两个钉子把木条钉在墙上时,木条就被固定住,其依据是两点确定一条直线,
故选:D.
7.解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
8.解:A、两点之间线段最短,原说法错误,故本选项不符合题意;
B、一个有理数,不是正数就是负数或零,原说法错误,故本选项不符合题意;
C、平角的两边在一条直线上,原说法错误,故本选项不符合题意;
D、整数和分数统称为有理数,原说法正确,故本选项符合题意;
故选:D.
9.解:①因为直线不可以度量,所以画直线AB=3cm是错误的;
②连接点A与点B的线段的长度,叫做A、B两点之间的距离,原说法错误;
③有公共端点是两条射线组成的图形叫做角,原说法错误;
④任何一个有理数都可以用数轴上的一个点来表示,原说法正确;
正确的有1个,
故选:B.
10.解:钟表在3点30分时,它的时针和分针所成的角是30°×2.5=75°,
故选:B.
11.解:30.45°=30°+0.45×60′=30°27′,
∵30°45′>30°27′,
∴30°45'>30.45°,
∴∠A>∠B,
故选:A.
12.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故选:B.
13.解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故选:C.
14.解:六边形从一个顶点可引出对角线:6﹣3=3(条),
故选:C.
15.解:∵最长的弦长为16cm,
∴⊙O的直径为16cm,
∴⊙O的半径为8cm.
故选:B.
二.填空题
16.解:图中线段有:AB、AC、AD、AE,BC、BD、BE,CD、CE、DE
共10条,
∵每条线段应印2种车票,
∴共需印10×2=20种车票.
故答案为:20.
17.解:①当四点共线时,则经过每两个点画一条直线,那么共可以画直线1条;
②当只有三点共线时,则经过每两个点画一条直线,那么共可以画直线4条;
③当每三点不共线时,则经过每两个点画一条直线,那么共可以画直线6条.
故答案为:1或4或6.
18.解:建造直隧道的目的可以用数学知识解释为:两点之间,线段最短.
故答案为:两点之间,线段最短.
19.解:如图1,∵AC=BD=1.5,AB=7,
∴CD=AB﹣AC﹣BD=4;
如图2,CD=AC+AB﹣BD=1.5+7﹣1.5=7;
如图3,CD=AB﹣AC+BD=7,
如图4,CD=AC+AB+BD=1.5+7+1.5=10,
综上所述,CD的长为4或7或10,
故答案为:4或7或10.
20.解:∠1可表示为∠BAC;∠CAD可表示为∠2;∠3可表示为∠ADC或∠D;∠4可表示为∠ACD;∠ABC可表示为∠5.
故答案为:∠BAC,∠2,∠ADC或∠D,∠ACD,∠5.
21.解:因为4点30分时针与分针相距1+=,
所以4点30分时针与分针所夹的锐角是30°×=45°,
故答案为:45.
22.解:由题意∠ABN=60°,所以A在B的北偏西60°的方向上.
故答案是:北偏西60°.
23.解:1.25°=1×60′+0.25×60′=60′+15′=75′,
5400″=(5400÷60)′=90′=(90÷60)°=1.5°,
故答案为:75;1.5.
24.解:设多边形有n条边,
则n﹣3=8,解得n=11.
故答案为:11.
25.解:如图,连接AB,CD,OE,OE交CD于J.
∵OC=AC,OD=DB,
∴CD∥AB,
∵=,
∴OE⊥AB,
∴CD⊥OE,
∵OC=OD=2,
∴CJ=OJ,
∵∠COD=90°,
∴CD===2,
∴S四边形OCED=?CD?OE=4,
∴S阴=S扇形AOB﹣S四边形OCED=?π?42﹣4=4π﹣4,
故答案为:4π﹣4.
三.解答题
26.解:(1)∵AB=8cm,M是AB的中点,
∴AM=AB=4cm,
∵AC=3cm,
∴CM=AM﹣AC=4﹣3=1(cm);
∵AB=8cm,AC=3cm,M是AB的中点,N是AC的中点,
∴AM=AB=4cm,AN=AC=1.5cm,
∴MN=AM﹣AN=4﹣1.5=2.5(cm);
(2)∵AC=m,BC=n,
∴AB=AC+BC=m+n,
∵M是AB的中点,N是AC的中点,
∴AM=AB=(m+n),AN=AC=m,
∴MN=AM﹣AN=(m+n)﹣m=n.
27.解:①图中共有线段:AB,AC,AD,BC,BD,CD;
故答案为:6;
②∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故答案为:=;
③∵BC=AC,且AC=6cm,
∴BC=×6=4(cm),AB=6﹣4=2(cm),
∴CD=2cm,
∴AD=2+2+4=8(cm).
故答案为:8.
28.解:(1)在角的内部作一条射线,共有三条射线,那么图中一共有×3×2=3个角;
(2)在角的内部作两条射线,共有四条射线,那么图中一共有=6个角;
(3)在角的内部作n条射线,共有(n+2)条射线,那么图中一共有(n+2)(n+1)个角.
29.解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
30.解:∵∠AOB=30°,∠COB=20°,
∴∠AOC=∠AOB+∠BOC=30°+20°=50°,
∵OC平分∠AOD,
∴∠AOC=∠COD=50°,
∴∠BOD=∠BOC+COD=20°+50°=70°.
基本平面图形
一.选择题
1.下列说法正确的是( )
A.延长直线AB到点C
B.延长射线AB到点C
C.延长线段AB到点C
D.射线AB与射线BA是同一条射线
2.下列说法不正确的有( )
①绝对值是本身的数是正数;
②符号不同的两个数互为相反数;
③两数相加,和一定大于任何一个加数;
④线段AB和线段BA表示的是同一条线段.
A.①③
B.②③
C.①②③
D.①②④
3.平面上有不同的三个点,经过其中任意两点画直线,一共可以画( )
A.1条
B.2条
C.3条
D.1条或3条
4.如图,在公路MN两侧分别有A1,A2…A7,七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
①车站的位置设在C点好于B点;
②车站的位置设在B点与C点之间公路上任何一点效果一样;
③车站位置的设置与各段小公路的长度无关;
④车站的位置设在BC段公路的最中间处要好于设在点B及点C处.
A.①③
B.③④
C.②③
D.②
5.如图1,A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小,图2中所示的C点即为所求的码头的位置,那么这样做的理由是( )
A.两直线相交只有一个交点
B.两点确定一条直线
C.两点之间,线段最短
D.经过一点有无数条直线
6.用两个钉子就可以把木条钉在墙上,其依据是( )
A.两点之间线段最短
B.两点之间直线最短
C.两点确定一条射线
D.两点确定一条直线
7.已知线段AB=9,点C是AB的中点,点D是AB的三等分点,则C,D两点间距离为( )
A.3
B.1.5
C.1.2
D.1
8.下列说法正确的是( )
A.两点之间直线最短
B.一个有理数,不是正数就是负数
C.平角是一条直线
D.整数和分数统称为有理数
9.下列语句中:正确的个数有( )
①画直线AB=3cm;
②连接点A与点B的线段,叫做A、B两点之间的距离;
③两条射线组成的图形叫角;
④任何一个有理数都可以用数轴上的一个点来表示.
A.0
B.1
C.2
D.3
10.钟表在3点30分时,它的时针和分针所成的角是( )
A.90°
B.75°
C.60°
D.45°
11.已知∠A=30°45',∠B=30.45°,则∠A( )∠B.(填“>”、“<”或“=”)
A.>
B.<
C.=
D.无法确定
12.如图,点O在直线AE上,OC平分∠AOE,∠DOB是直角.若∠1=25°,那么∠AOB的度数是( )
A.65°
B.25°
C.90°
D.115°
13.如图,点O在直线AB上,过O作射线OC,∠BOC=100°,一直角三角板的直角顶点与点O重合,边OM与OB重合,边ON在直线AB的下方.若三角板绕点O按每秒10°的速度沿逆时针方向旋转一周,在旋转的过程中,第t秒时,直线ON恰好平分锐角∠AOC,则t的值为( )
A.5
B.4
C.5或23
D.4或22
14.过六边形的一个顶点的对角线共有( )条.
A.1
B.2
C.3
D.4
15.已知⊙O中,最长的弦长为16cm,则⊙O的半径是( )
A.4cm
B.8cm
C.16cm
D.32cm
二.填空题
16.如图所示是一段火车路线图,A、B、C、D、E是五个火车站,在这条线路上往返行车需要印制
种火车票.
17.平面上有四个点,经过其中每两个点画一条直线,那么一共可以画直线
条.
18.西成高铁是中国首条穿越秦岭的高速铁路,大大减少了人们从西安到四川成都的时间,实现了人们“早上游大雁塔,晚上逛宽窄巷”的美好愿望.建造直隧道的目的可以用数学知识解释为
.
19.已知点C,D在直线AB上,且AC=BD=1.5,若AB=7,则CD的长为
.
20.将图中的角用不同方法表示出来,并填写下表:
∠1
∠3
∠4
∠CAD
∠B
21.4点30分时,时钟的时针与分针所夹的锐角是
度.
22.A、B两地的位置如图所示,则A位于B的
方向上.
23.1.25°=
分,5400″=
度.
24.若从一个n边形的一个顶点出发,最多可以引8条对角线,则n=
.
25.如图,在扇形AOB中,∠AOB=90°,点C为半径OA的中点,以点O为圆心,OC的长为半径作弧CD交OB于点D,点E为弧AB的中点,连接CE、DE.若OA=4,则阴影部分的面积为
.
三.解答题
26.如图,线段AB=8cm,C是线段AB上一点,M是AB的中点,N是AC的中点.
(1)AC=3cm,求线段CM、NM的长;
(2)若线段AC=m,线段BC=n,求MN的长度(m<n用含m,n的代数式表示).
27.如图:A、B、C、D四点在同一直线上,若AB=CD.
①图中共有
条线段;
②比较线段的大小:AC
BD(填“>”、“=”或“<”);
③若BC=AC,且AC=6cm,则AD的长为
cm;
28.(1)如图①,过角的顶点在角的内部作一条射线,那么图中一共有多少个角?
(2)如图②,过角的顶点在角的内部作两条射线,那么图中一共有多少个角?
(3)如图③,过角的顶点在角的内部作n条射线,那么图中一共有多少个角?
29.如图,B岛在A岛的南偏西40°方向,C岛在A岛的南偏东15°方向,C岛在B岛的北偏东80°方向,求从C岛看A,B两岛的视角∠ACB的度数.
30.已知:如图,∠AOB=30°,∠COB=20°,OC平分∠AOD,求∠BOD的度数.
参考答案
一.选择题
1.解:A、直线可以沿两个方向无限延伸,故不能说延长直线AB,故本选项不符合题意;
B、射线可沿延伸方向无限延伸,故不能说延长射线AB,故本选项不符合题意;
C、线段不能延伸,可以说延长线段AB到点C,故本选项符合题意;
D、射线AB与射线BA不是同一条射线,故本选项不符合题意;
故选:C.
2.解:①绝对值是本身的数是非负数,故①符合题意;
②符号不同的两个数不一定是互为相反数,故②符合题意;
③两数相加,和不一定大于任何一个加数,故③符合题意;
④线段AB和线段BA表示的是同一条线段,故④不符合题意,
故选:C.
3.解:如图,经过其中任意两点画直线可以画3条直线或1条直线,
故选:D.
4.解:①通过测量发现车站的位置设在C点好于B点,故原来的结论正确;
②车站设在B点与C点之间公路上,车站朝M方向始终有4个工厂,车站朝N方向始终有3个工厂,所以在这一段任何一点,效果一样,故原来的结论错误;
③工厂到车站的距离是线段的长,和各段的弯曲的小公路无关,故原来的结论正确;
④车站的位置设在BC段公路的最中间处与设在点B及点C处一样好,故原来的结论错误.
故选:A.
5.解:A,B两个村庄在一条河l(不计河的宽度)的两侧,现要建一座码头,使它到A、B两个村庄的距离之和最小,图2中所示的C点即为所求的码头的位置,那么这样做的理由是两点之间,线段最短,
故选:C.
6.解:用两个钉子把木条钉在墙上时,木条就被固定住,其依据是两点确定一条直线,
故选:D.
7.解:∵点C是AB的中点,AB=9,
∴AC=CB=AB=4.5,
当点D是AB的三等分点,点D在线段BC上时,BD=AB=3,
∴CD=4.5﹣3=1.5,
当点D是AB的三等分点,点D′在线段AC上时,AD′=AB=3,
∴CD′=4.5﹣3=1.5,
故选:B.
8.解:A、两点之间线段最短,原说法错误,故本选项不符合题意;
B、一个有理数,不是正数就是负数或零,原说法错误,故本选项不符合题意;
C、平角的两边在一条直线上,原说法错误,故本选项不符合题意;
D、整数和分数统称为有理数,原说法正确,故本选项符合题意;
故选:D.
9.解:①因为直线不可以度量,所以画直线AB=3cm是错误的;
②连接点A与点B的线段的长度,叫做A、B两点之间的距离,原说法错误;
③有公共端点是两条射线组成的图形叫做角,原说法错误;
④任何一个有理数都可以用数轴上的一个点来表示,原说法正确;
正确的有1个,
故选:B.
10.解:钟表在3点30分时,它的时针和分针所成的角是30°×2.5=75°,
故选:B.
11.解:30.45°=30°+0.45×60′=30°27′,
∵30°45′>30°27′,
∴30°45'>30.45°,
∴∠A>∠B,
故选:A.
12.解:∵点O在直线AE上,OC平分∠AOE,
∴∠AOC=∠COE=90°,
∵∠DOB是直角,∠1=25°,
∴∠BOC=∠DOB﹣∠1=90°﹣25°=65°,
∵∠AOB+∠BOC=∠AOC=90°
∴∠AOB=90°﹣∠BOC=90°﹣65°=25°.
故选:B.
13.解:∵∠BOC=100°,
∴∠AOC=80°,
当直线ON恰好平分锐角∠AOC时,如下图:
∠BON=∠AOC=40°,
此时,三角板旋转的角度为90°﹣40°=50°,
∴t=50°÷10°=5;
当ON在∠AOC的内部时,如下图:
三角板旋转的角度为360°﹣90°﹣40°=230°,
∴t=230°÷10°=23;
∴t的值为:5或23.
故选:C.
14.解:六边形从一个顶点可引出对角线:6﹣3=3(条),
故选:C.
15.解:∵最长的弦长为16cm,
∴⊙O的直径为16cm,
∴⊙O的半径为8cm.
故选:B.
二.填空题
16.解:图中线段有:AB、AC、AD、AE,BC、BD、BE,CD、CE、DE
共10条,
∵每条线段应印2种车票,
∴共需印10×2=20种车票.
故答案为:20.
17.解:①当四点共线时,则经过每两个点画一条直线,那么共可以画直线1条;
②当只有三点共线时,则经过每两个点画一条直线,那么共可以画直线4条;
③当每三点不共线时,则经过每两个点画一条直线,那么共可以画直线6条.
故答案为:1或4或6.
18.解:建造直隧道的目的可以用数学知识解释为:两点之间,线段最短.
故答案为:两点之间,线段最短.
19.解:如图1,∵AC=BD=1.5,AB=7,
∴CD=AB﹣AC﹣BD=4;
如图2,CD=AC+AB﹣BD=1.5+7﹣1.5=7;
如图3,CD=AB﹣AC+BD=7,
如图4,CD=AC+AB+BD=1.5+7+1.5=10,
综上所述,CD的长为4或7或10,
故答案为:4或7或10.
20.解:∠1可表示为∠BAC;∠CAD可表示为∠2;∠3可表示为∠ADC或∠D;∠4可表示为∠ACD;∠ABC可表示为∠5.
故答案为:∠BAC,∠2,∠ADC或∠D,∠ACD,∠5.
21.解:因为4点30分时针与分针相距1+=,
所以4点30分时针与分针所夹的锐角是30°×=45°,
故答案为:45.
22.解:由题意∠ABN=60°,所以A在B的北偏西60°的方向上.
故答案是:北偏西60°.
23.解:1.25°=1×60′+0.25×60′=60′+15′=75′,
5400″=(5400÷60)′=90′=(90÷60)°=1.5°,
故答案为:75;1.5.
24.解:设多边形有n条边,
则n﹣3=8,解得n=11.
故答案为:11.
25.解:如图,连接AB,CD,OE,OE交CD于J.
∵OC=AC,OD=DB,
∴CD∥AB,
∵=,
∴OE⊥AB,
∴CD⊥OE,
∵OC=OD=2,
∴CJ=OJ,
∵∠COD=90°,
∴CD===2,
∴S四边形OCED=?CD?OE=4,
∴S阴=S扇形AOB﹣S四边形OCED=?π?42﹣4=4π﹣4,
故答案为:4π﹣4.
三.解答题
26.解:(1)∵AB=8cm,M是AB的中点,
∴AM=AB=4cm,
∵AC=3cm,
∴CM=AM﹣AC=4﹣3=1(cm);
∵AB=8cm,AC=3cm,M是AB的中点,N是AC的中点,
∴AM=AB=4cm,AN=AC=1.5cm,
∴MN=AM﹣AN=4﹣1.5=2.5(cm);
(2)∵AC=m,BC=n,
∴AB=AC+BC=m+n,
∵M是AB的中点,N是AC的中点,
∴AM=AB=(m+n),AN=AC=m,
∴MN=AM﹣AN=(m+n)﹣m=n.
27.解:①图中共有线段:AB,AC,AD,BC,BD,CD;
故答案为:6;
②∵AB=CD,
∴AB+BC=CD+BC,
∴AC=BD,
故答案为:=;
③∵BC=AC,且AC=6cm,
∴BC=×6=4(cm),AB=6﹣4=2(cm),
∴CD=2cm,
∴AD=2+2+4=8(cm).
故答案为:8.
28.解:(1)在角的内部作一条射线,共有三条射线,那么图中一共有×3×2=3个角;
(2)在角的内部作两条射线,共有四条射线,那么图中一共有=6个角;
(3)在角的内部作n条射线,共有(n+2)条射线,那么图中一共有(n+2)(n+1)个角.
29.解:如图,由题意得:BE∥AD,∠BAD=40°,∠CAD=15°,∠EBC=80°,
∴∠EBA=∠BAD=40°,
∴∠BAC=∠BAD+∠CAD=40°+15°=55°,
∴∠CBA=∠EBC﹣∠EBA=80°﹣40°=40°,
∴∠ACB=180°﹣∠BAC﹣∠ABC
=180°﹣55°﹣40°=85°,
答:从C岛看A,B两岛的视角∠ACB的度数为85°.
30.解:∵∠AOB=30°,∠COB=20°,
∴∠AOC=∠AOB+∠BOC=30°+20°=50°,
∵OC平分∠AOD,
∴∠AOC=∠COD=50°,
∴∠BOD=∠BOC+COD=20°+50°=70°.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
