人教版八年级数学上册12.1全等三角形知识水平测试题(2小节 Word版 含解析)
文档属性
| 名称 | 人教版八年级数学上册12.1全等三角形知识水平测试题(2小节 Word版 含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 786.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 19:20:09 | ||
图片预览


文档简介
人教版八年级数学上册第12章知识水平测试题含答案
12.1
全等三角形
一.选择题
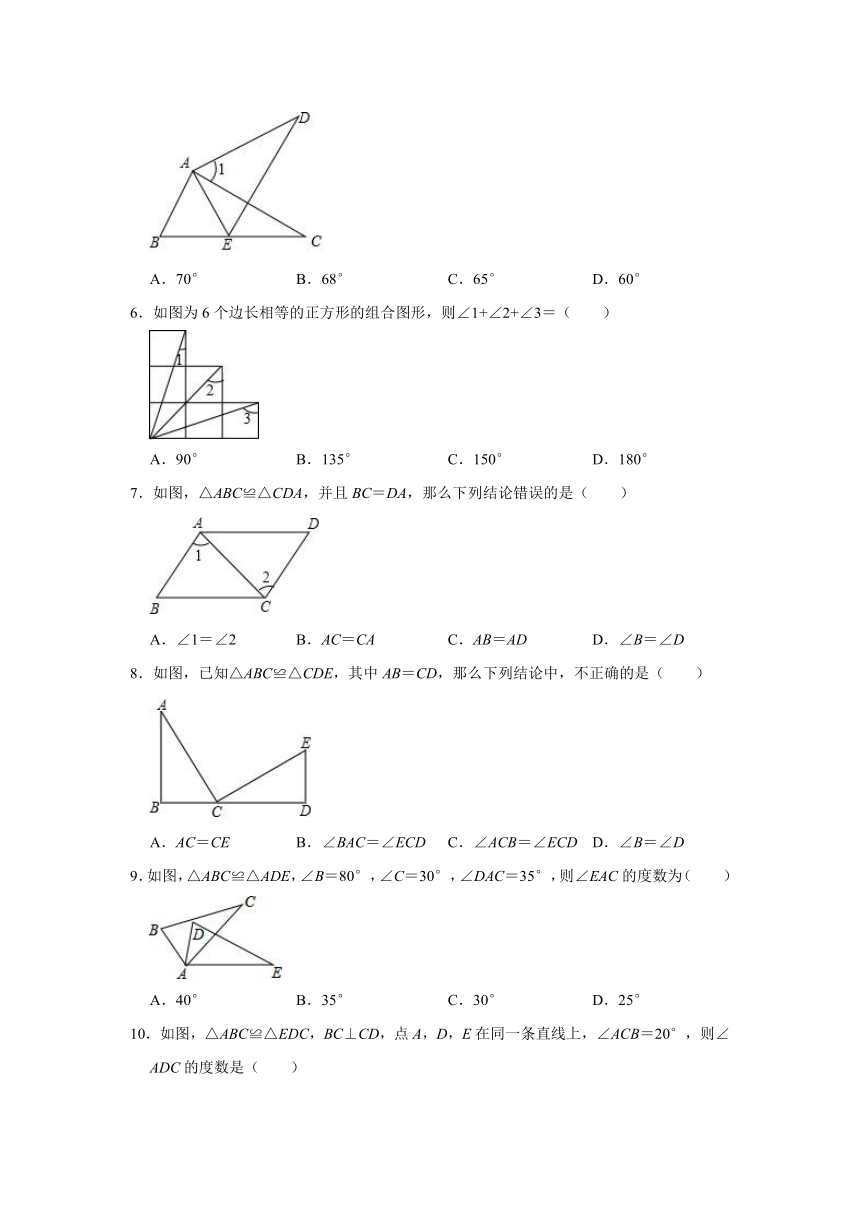
1.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
3.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°
B.180°
C.210°
D.225°
4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
5.如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
A.70°
B.68°
C.65°
D.60°
6.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90°
B.135°
C.150°
D.180°
7.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.AC=CA
C.AB=AD
D.∠B=∠D
8.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( )
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
9.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
10.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
二.填空题
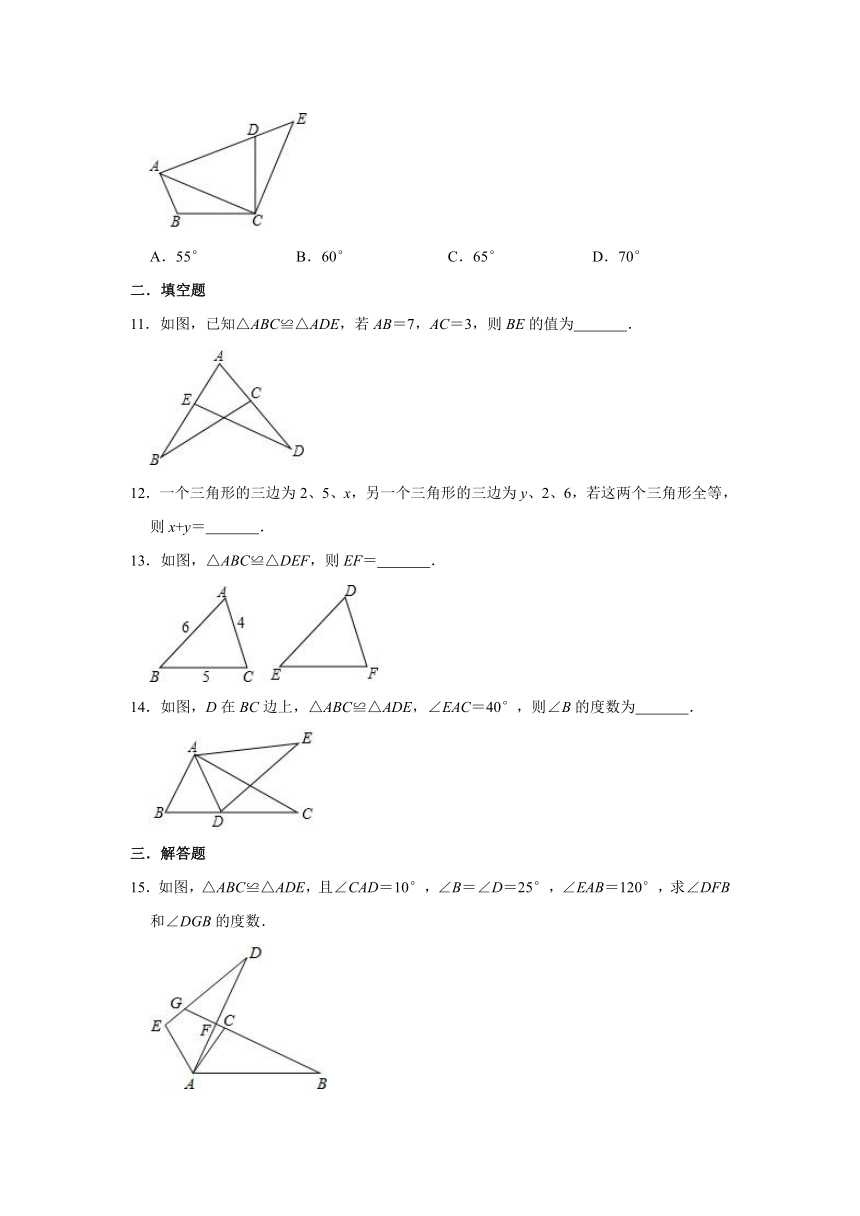
11.如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为
.
12.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
13.如图,△ABC≌△DEF,则EF=
.
14.如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为
.
三.解答题
15.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
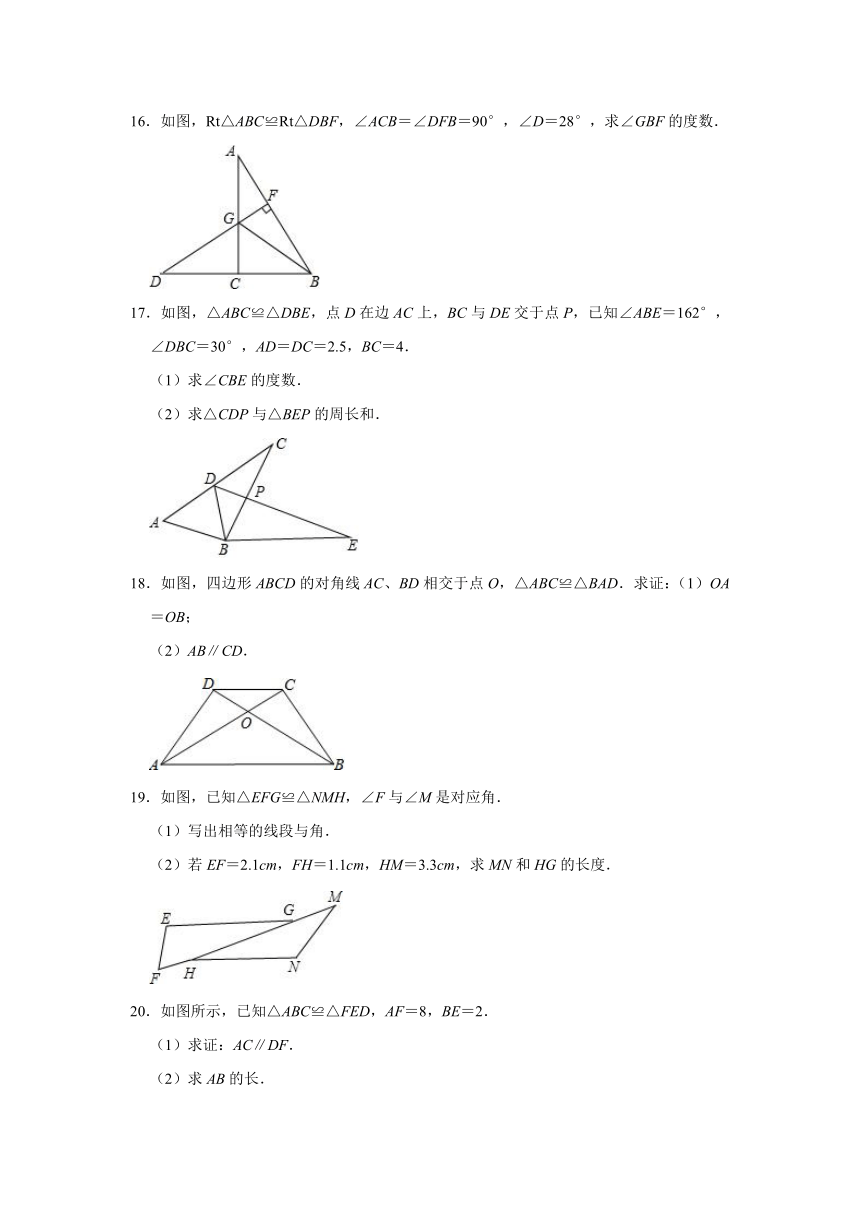
16.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.
17.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
18.如图,四边形ABCD的对角线AC、BD相交于点O,△ABC≌△BAD.求证:(1)OA=OB;
(2)AB∥CD.
19.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出相等的线段与角.
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
20.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF.
(2)求AB的长.
21.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
22.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
23.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
参考答案
一.选择题
1.解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
2.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
3.解:
由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
故选:B.
4.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选:D.
5.解:∵△ABC≌△AED,
∴∠AED=∠B,AE=AB,∠BAC=∠EAD,
∴∠1=∠BAE=40°,
∴△ABE中,∠B==70°,
∴∠AED=70°,
故选:A.
6.解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠1+∠3=90°,
又∵∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:B.
7.解:∵△ABC≌△CDA,BC=DA
∴AB=CD,∠1=∠2,AC=CA,∠B=∠D,
∴A,B,D是正确的,C、AB=AD是错误的.
故选:C.
8.解:∵△ABC≌△CDE,AB=CD
∴∠ACB=∠CED,AC=CE,∠BAC=∠ECD,∠B=∠D
∴第三个选项∠ACB=∠ECD是错的.
故选:C.
9.解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选:B.
10.解:∵,△ABC≌△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠ACD=90°﹣20°=70°,
∵点A,D,E在同一条直线上,
∴∠ADC+∠EDC=180°,
∵∠EDC+∠E+∠DCE=180°,
∴∠ADC=∠E+20°,
∵∠ACE=90°,AC=CE
∴∠DAC+∠E=90°,∠E=∠DAC=45°
在△ADC中,∠ADC+∠DAC+∠DCA=180°,
即45°+70°+∠ADC=180°,
解得:∠ADC=65°,
故选:C.
二.填空题
11.解:∵△ABC≌△ADE,
∴AE=AC,
∵AB=7,AC=3,
∴BE=AB﹣AE=AB﹣AC=7﹣3=4.
故答案为:4.
12.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
13.解:∵△ABC≌△DEF,
∴BC=EF
则EF=5.
故答案为:5.
14.解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
三.解答题
15.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
16.解:∵Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,
∴BC=BF,BD=BA,
∴CD=AF,
在△DGC和△AGF中,
,
∴△DGC≌△AGF,
∴GC=GF,又∠ACB=∠DFB=90°,
∴∠CBG=∠FBG,
∴∠GBF=(90°﹣28°)÷2=31°.
17.解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
18.证明:(1)∵△ABC≌△BAD,
∴∠CAB=∠DBA,
∴OA=OB.
(2)∵△ABC≌△BAD,
∴AC=BD,
又∵OA=OB,
∴AC﹣OA=BD﹣OB,
即:OC=OD,
∴∠OCD=∠ODC,
∵∠AOB=∠COD,∠CAB=,∠ACD=,
∴∠CAB=∠ACD,
∴AB∥CD.
19.解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
20.证明:(1)∵△ABC≌△FED,
∴∠A=∠F.
∴AC∥DF.
(2)∵△ABC≌△FED,
∴AB=EF.
∴AB﹣EB=EF﹣EB.
∴AE=BF.
∵AF=8,BE=2
∴AE+BF=8﹣2=6
∴AE=3
∴AB=AE+BE=3+2=5
21.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
22.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
23.解:(1)其他对应角为:∠BAF和∠DCE,∠AFB和∠CED;
其他对应边为:AB和CD是对应边,BF和DE是对应边;
(2)∵△ABF≌△CDE,∠B=30°,
∴∠D=∠B=30°,
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=30°+40°=70°;
(3)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,
∴DF=BE,
∵BD=10,EF=2,
∴DF=BE=4,
∴BF=BE+EF=4+2=6.
12.2
全等三角形
一、选择题
1.
如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D
B.∠C=∠E
C.∠1=∠2
D.∠3=∠4
2.
如图,已知∠1=∠2,欲证△ABD≌△ACD,还需从下列条件中补选一个,则错误的选项是( )
A.∠ADB=∠ADC
B.∠B=∠C
C.DB=DC
D.AB=AC
3.
(2019?临沂)如图,是上一点,交于点,,,若,,则的长是
A.0.5
B.1
C.1.5
D.2
4.
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
5.
如图所示,在△ABC和△ABD中,∠C=∠D=90°,要利用“HL”判定Rt△ABC≌Rt△ABD成立,还需要添加的条件是
( )
A.∠BAC=∠BAD
B.BC=BD或AC=AD
C.∠ABC=∠ABD
D.AC=BD
6.
如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
7.
如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
8.
如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c
B.b+c
C.a-b+c
D.a+b-c
9.
观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC
B.∠C=∠EAC
C.AE∥BC
D.∠DAE=∠B
10.
如图,AB⊥BC,BE⊥AC,垂足分别为B,E,∠1=∠2,AD=AB,则下列结论正确的是( )
A.∠1=∠EFD
B.BE=EC
C.BF=CD
D.FD∥BC
二、填空题
11.
要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
12.
如图K-10-10,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,ED与AB相交于点G.若∠ACD=40°,则∠AGD=________°.
13.
如图,小明和小丽为了测量池塘两端A,B两点之间的距离,先取一个可以直接到达点A和点B的点C,沿AC方向走到点D处,使CD=AC;再用同样的方法确定点E,使CE=BC.若量得DE的长为60米,则池塘两端A,B两点之间的距离是______米.
14.
如图,在中,,以顶点为圆心,适当长度为半径画弧,分别交于点,再分别以点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则__________.
15.
如图,在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,则AE=________cm.
三、解答题
16.
如图,AB=AD,BC=DC,点E在AC上.
求证:(1)AC平分∠BAD;
(2)BE=DE.
17.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
图① 图②
18.
(2019?桂林)如图,,点在上.
(1)求证:平分;
(2)求证:.
19.
如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
20.
如图①,若AD=CD,AB=CB,则四边形ABCD是筝形.
(1)在同一平面内,△ABC与△ADE按图②所示的方式放置,其中∠B=∠D=90°,AB=AD,BC与DE相交于点F,请你判断四边形ABFD是不是筝形,并说明理由;
(2)请你结合图①,写出筝形的一个判定方法(定义除外):在四边形ABCD中,若________________,则四边形ABCD是筝形.
人教版
八年级数学
12.2
全等三角形
针对训练
-答案
一、选择题
1.
【答案】C [解析]
还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
2.
【答案】C [解析]
当添加条件A时,可用“ASA”证明△ABD≌△ACD;当添加条件B时,可用“AAS”证明△ABD≌△ACD;当添加条件D时,可用“SAS”证明△ABD≌△ACD;当添加条件C时,不能证明△ABD≌△ACD.
3.
【答案】B
【解析】∵,∴,,
在和中,,∴,∴,
∵,∴.故选B.
4.
【答案】C [解析]
选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
5.
【答案】B [解析]
要添加的条件为BC=BD或AC=AD.理由:若添加的条件为BC=BD,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL).
6.
【答案】C [解析]
①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
7.
【答案】C [解析]
A.∠A=∠D,∠ABC=∠DCB,BC=BC,符合“AAS”,即能推出△ABC≌△DCB,故本选项不符合题意;
B.∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合“ASA”,即能推出△ABC≌△DCB,故本选项不符合题意;
C.∠ABC=∠DCB,AC=DB,BC=BC,不符合全等三角形的判定条件,即不能推出△ABC≌△DCB,故本选项符合题意;
D.AB=DC,∠ABC=∠DCB,BC=CB,符合“SAS”,即能推出△ABC≌△DCB,故本选项不符合题意.
故选C.
8.
【答案】D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠CED=∠AFB=90°,∠A=∠C.又∵AB=CD,∴△CED≌△AFB.∴AF=CE=a,DE=BF=b,DF=DE-EF=b-c.∴AD=AF+DF=a+b-c.故选D.
9.
【答案】A [解析]
根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
10.
【答案】D [解析]
在△AFD和△AFB中,
∴△AFD≌△AFB.
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
∴∠BEC=∠ABC=90°.
∴∠ABF+∠EBC=90°,∠C+∠EBC=90°.
∴∠ADF=∠ABF=∠C.
∴FD∥BC.
二、填空题
11.
【答案】20
12.
【答案】40 [解析]
在△ABC和△DEC中,
∴△ABC≌△DEC(SSS).
∴∠A=∠D.
又∵∠AFG=∠DFC,
∴∠AGD=∠ACD=40°.
13.
【答案】60 [解析]
在△ACB和△DCE中,
∴△ACB≌△DCE(SAS).∴DE=AB.
∵DE=60米,∴AB=60米.
14.
【答案】
【解析】由作法得平分,
∵,,∴,
∴,∴,
在中,,∴,
∴.故答案为:.
15.
【答案】3 [解析]
∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2
cm,EF=5
cm,
∴AE=5-2=3(cm).
三、解答题
16.
【答案】
证明:(1)在△ABC与△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC,
即AC平分∠BAD.
(2)由(1)知∠BAE=∠DAE.
在△BAE与△DAE中,
∴△BAE≌△DAE(SAS).
∴BE=DE.
17.
【答案】
(1)证明:如图①,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF,OB=OC,
解图①
∴Rt△OEB≌Rt△OFC,
∴∠B=∠C,从而AB=AC.
(2)证明:如图②,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF.
在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,
解图②
∴Rt△OEB≌Rt△OFC.
∴∠OBE=∠OCF,
又由OB=OC知∠OBC=∠OCB,
∴∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立.
(注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图③)
解图③
18.
【答案】
(1)在与中,,
∴,
∴,
即平分.
(2)由(1),
在与中,得,
∴,
∴.
19.
【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
20.
【答案】
解:(1)四边形ABFD是筝形.
理由:连接AF.
在Rt△AFB和Rt△AFD中,
∴Rt△AFB≌Rt△AFD(HL).∴BF=DF.
又∵AB=AD,∴四边形ABFD是筝形.
(2)答案不唯一,如AD=CD,∠ADB=∠CDB
12.3角平分线的性质
一.选择题
1.已知:在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=20,且BD:DC=3:2,则点D到AB边的距离为( )
A.8
B.12
C.10
D.15
2.如图已知OC平分∠AOB,P是距离是OC上一点,PH⊥OB于点H,若PH=5,则点
P到射线OA的距离是( )
A.6
B.5
C.4
D.3
3.如图,四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=8,BD=13,BC=12,则四边形ABCD的面积为( )
A.30
B.40
C.50
D.60
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15
B.12
C.10
D.14
5.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,∠CAB和∠ABC的平分线交于点O,OM⊥BC于点M,则OM的长为( )
A.1
B.2
C.3
D.4
6.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.1.5
C.2
D.2.5
7.如图,AD∥BC,BG,AG分别平分∠ABC与∠BAD,GH⊥AB,GH=5,则AD与BC之间的距离是( )
A.5
B.8
C.10
D.15
8.下列关于几何画图的语句,正确的是( )
A.延长射线AB到点C,使BC=2AB
B.点P在线段AB上,点Q在直线AB的反向延长线上
C.将射线OA绕点O旋转,当终止位置OB与起始位置OA成一条直线时形成平角
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b
9.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=5,AB=12,则△ABD的面积是( )
A.15
B.30
C.45
D.60
10.如图,点M在线段BC上,点E和N在线段AC上,EM∥AB,BE和MN分别平分∠ABC和∠EMC.下列结论中不正确的是( )
A.∠MBE=∠MEB
B.MN∥BE
C.S△BEM=S△BEN
D.∠MBN=∠MNB
二.填空题
11.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=5cm,BD:DC=3:2,则点D到AB的距离为
.
12.如图点D是△ABC的两外角平分线的交点,下列说法:
①AD=CD;
②AB=AC;
③D到AB、BC所在直线的距离相等;
@点D在∠B的平分线上;
其中正确的说法的序号是
.
13.已知如图,OP平分∠MON,PA⊥ON于点A,PA=4,点Q是射线OM上的一个动点,则线段PQ的最小值是
.
14.在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N中在∠AOB的平分线上是
点.
15.如图,已知△ABC的周长是16.MB和MC分别平分∠ABC和∠ACB.过点M作BC的垂线交BC于点D,且MD=4.则△ABC的面积是
.
三.解答题
16.如图,直线AC分别与射线DE交于A,与射线BF交于C,连接AB,连接DC,∠1+∠2=180°,AD=BC.若DC平分∠ACF,证明AB平分∠EAC.
17.如图,三角形ABC中,点D在AC上.
(1)请你过点D做DE平行BC,交AB于E.如果点E在∠C的平分线上,∠C=44°,那么∠DEC=
.
18.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
19.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
参考答案与试题解析
一.选择题
1.【解答】解:∵BC=20,BD:DC=3:2,
∴CD=8,
∵∠C=90°
AD平分∠BAC
∴D到边AB的距离=CD=8.
故选:A.
2.【解答】解:作PQ⊥OA于Q,如图,
∵OC为∠AOB的平分线,PH⊥OB,PQ⊥OA,
∴PQ=PH=5,
即点P到射线OA的距离为5.
故选:B.
3.【解答】解:
过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,
∵∠BCD=90°,BD平分∠ABC,
∴DE=DC,
在Rt△BCD中,由勾股定理得:CD===5,
∴DE=5,
在Rt△BED中,由勾股定理得:BE===12,
∵AB=8,
∴AE=BE﹣AB=12﹣8=4,
∴四边形ABCD的面积S=S△BCD+S△BED﹣S△AED
=+﹣
=+﹣
=50,
故选:C.
4.【解答】解:过点E作EF⊥AB于点F,如图:
∵BD是AC边上的高,
∴ED⊥AC,
又∵AE平分∠CAB,DE=3,
∴EF=3,
∵AB=8,
∴△ABE的面积为:8×3÷2=12.
故选:B.
5.【解答】解:过O作OD⊥AC于D,OE⊥AB于E,
∵AO平分∠CAB,OB平分∠ABC,
∴OD=OE=OM,
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,
∴S△ABC=ACBC=×ABOE+ACOD+BCOM,
∴=+OM+,
∴OM=2,
故选:B.
6.【解答】解:过点D作DE⊥BC于E,则DE即为DP的最小值,
∵∠BAD=∠BDC=90°,∠ADB=∠C,
∴∠ABD=∠CBD,
∵∠ABD=∠CBD,DA⊥AB,DE⊥BC,
∴DE=AD=2,
故选:C.
7.【解答】解:作GE⊥AD于E,EG的延长线交BC于F,如图,则∠DEG=90°,
∵AD∥BC,
∴∠BFG=∠DEG=90°,
∴EF⊥BC,
∵BG,AG分别平分∠ABC与∠BAD,
∴GE=GH=5,GF=GH=5,
∴EF=5+5=10,
即AD与BC之间的距离为10.
故选:C.
8.【解答】解:A.延长射线AB到点C,使BC=2AB,
因为射线不能延长,
所以A选项错误,不符合题意;
B.因为直线不能反向延长,
所以B选项错误,不符合题意;
C.将射线OA绕点O旋转,当终止位置OB与起始位置OA成一条直线时形成平角.
C选项正确,符号题意;
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b或=a﹣b.
所以D选项错误,不符合题意.
故选:C.
9.【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,
∴DC⊥AC,
∵DE⊥AB,DC⊥AC,
∴DE=DC=5,
∴△ABD的面积=×AB×DE=×12×5=30,
故选:B.
10.【解答】解:∵EM∥AB,BE和MN分别平分∠ABC和∠EMC,
∴∠MEB=∠ABE,∠ABC=∠EMC,∠ABE=∠MBE,∠EMN=∠NMC,
∴∠MEB=∠MBE(故A正确),∠EBM=∠NMC,
∴MN∥BE(故B正确),
∴MN和BE之间的距离处处相等,
∴S△BEM=S△BEN(故C正确),
∵∠MNB=∠EBN,而∠EBN和∠MBN的关系不知,
∴∠MBN和∠MNB的关系无法确定,故D错误,
故选:D.
二.填空题
11.【解答】解:作DE⊥AB于E,如图,
∵BC=5cm,BD:DC=3:2,
∴BD=3,CD=2,
∵AD是△ABC的角平分线,
∴DC=DE=2,
即点D到AB的距离为2.
故答案为2.
12.【解答】解:AD与CD不能确定相等,AB与AC也不能确定相等,所以①②错误;
作DE⊥BA于E,DF⊥BC于F,DH⊥AC于H,如图,
∵AD平分∠EAC,
∴DE=DH,
同理可得DH=DF,
∴DE=DF,
即D到AB、BC所在直线的距离相等,所以③正确;
∴点D在∠B的平分线上;所以④正确.
故答案为③④.
13.【解答】解:当PQ⊥OM时,PQ有最小值.
∵OP平分∠MON,PA⊥ON于点A,PA=4,
∴PQ=PA=4,
故答案为4.
14.【解答】解:点P、Q、M、N中在∠AOB的平分线上是Q点.
故答案为Q.
15.【解答】解:连接AM,过M作ME于E,MF⊥AC于F,
∵MD⊥BC,MB和MC分别平分∠ABC和∠ACB,MD=4,
∴ME=MD=4,MF=MD=4,
∵△ABC的周长是16,
∴AB+BC+AC=16,
∴△ABC的面积S=S△ABM+S△BCM+S△ACM
=+
=
=2AB+2BC+2AC
=2(AB+BC+AC)
=2×16
=32,
故答案为:32.
三.解答题
16.【解答】证明:∠1+∠2=180°,∠1+∠ACB=180°,
∴∠2=∠ACB,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD为平行四边形,
∴DC∥AB,
∴∠DCF=∠B,∠DCA=∠BAC,
∵DC平分∠ACF,
∴∠DCF=∠DCA,
∴∠B=∠BAC,
∵AD∥BC,
∴∠EAB=∠B,
∴∠BAC=∠EAB,即AB平分∠EAC.
17.【解答】解:(1)如图1所示:
作∠ADE=∠C交AB于E,DE即为所求;
(2)如图2所示:
∵DE∥BC,
∴∠DEC=∠BCE,
∵EC平分∠ACB,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DC=DE,
∴△DEC是等腰三角形,
∴∠DEC=∠C=22°;
故答案为:22°.
18.【解答】解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DFAC=×2×4=4.
19.【解答】解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×B
12.1
全等三角形
一.选择题
1.如图,△ABC≌△AEF,AB=AE,∠B=∠E,则对于结论①AC=AF,②∠FAB=∠EAB,③EF=BC,④∠EAB=∠FAC,其中正确结论的个数是( )
A.1个
B.2个
C.3个
D.4个
2.下列说法正确的是( )
A.形状相同的两个三角形全等
B.面积相等的两个三角形全等
C.完全重合的两个三角形全等
D.所有的等边三角形全等
3.如图是由4个相同的小正方形组成的网格图,其中∠1+∠2等于( )
A.150°
B.180°
C.210°
D.225°
4.如图,已知△ABE≌△ACD,∠1=∠2,∠B=∠C,不正确的等式是( )
A.AB=AC
B.∠BAE=∠CAD
C.BE=DC
D.AD=DE
5.如图,△ABC≌△AED,点E在线段BC上,∠1=40°,则∠AED的度数是( )
A.70°
B.68°
C.65°
D.60°
6.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=( )
A.90°
B.135°
C.150°
D.180°
7.如图,△ABC≌△CDA,并且BC=DA,那么下列结论错误的是( )
A.∠1=∠2
B.AC=CA
C.AB=AD
D.∠B=∠D
8.如图,已知△ABC≌△CDE,其中AB=CD,那么下列结论中,不正确的是( )
A.AC=CE
B.∠BAC=∠ECD
C.∠ACB=∠ECD
D.∠B=∠D
9.如图,△ABC≌△ADE,∠B=80°,∠C=30°,∠DAC=35°,则∠EAC的度数为( )
A.40°
B.35°
C.30°
D.25°
10.如图,△ABC≌△EDC,BC⊥CD,点A,D,E在同一条直线上,∠ACB=20°,则∠ADC的度数是( )
A.55°
B.60°
C.65°
D.70°
二.填空题
11.如图,已知△ABC≌△ADE,若AB=7,AC=3,则BE的值为
.
12.一个三角形的三边为2、5、x,另一个三角形的三边为y、2、6,若这两个三角形全等,则x+y=
.
13.如图,△ABC≌△DEF,则EF=
.
14.如图,D在BC边上,△ABC≌△ADE,∠EAC=40°,则∠B的度数为
.
三.解答题
15.如图,△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=120°,求∠DFB和∠DGB的度数.
16.如图,Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,∠D=28°,求∠GBF的度数.
17.如图,△ABC≌△DBE,点D在边AC上,BC与DE交于点P,已知∠ABE=162°,∠DBC=30°,AD=DC=2.5,BC=4.
(1)求∠CBE的度数.
(2)求△CDP与△BEP的周长和.
18.如图,四边形ABCD的对角线AC、BD相交于点O,△ABC≌△BAD.求证:(1)OA=OB;
(2)AB∥CD.
19.如图,已知△EFG≌△NMH,∠F与∠M是对应角.
(1)写出相等的线段与角.
(2)若EF=2.1cm,FH=1.1cm,HM=3.3cm,求MN和HG的长度.
20.如图所示,已知△ABC≌△FED,AF=8,BE=2.
(1)求证:AC∥DF.
(2)求AB的长.
21.如图,若△OAD≌△OBC,且∠0=65°,∠BEA=135°,求∠C的度数.
22.如图,已知△ABC≌△DEF,∠A=85°,∠B=60°,AB=8,EH=2.
(1)求角F的度数与DH的长;
(2)求证:AB∥DE.
23.如图,△ABF≌△CDE,∠B和∠D是对应角,AF和CE是对应边.
(1)写出△ABF和△CDE的其他对应角和对应边;
(2)若∠B=30°,∠DCF=40°,求∠EFC的度数;
(3)若BD=10,EF=2,求BF的长.
参考答案
一.选择题
1.解:∵△ABC≌△AEF,
∴AC=AF,故①正确;
∠EAF=∠BAC,
∴∠FAC=∠EAB≠∠FAB,故②错误;
EF=BC,故③正确;
∠EAB=∠FAC,故④正确;
综上所述,结论正确的是①③④共3个.
故选:C.
2.解:A、形状相同的两个三角形全等,说法错误,应该是形状相同且大小也相同的两个三角形全等;
B、面积相等的两个三角形全等,说法错误;
C、完全重合的两个三角形全等,说法正确;
D、所有的等边三角形全等,说法错误;
故选:C.
3.解:
由题意得:AB=ED,BC=DC,∠D=∠B=90°,
∴△ABC≌△EDC(SAS),
∴∠BAC=∠1,
∠1+∠2=180°.
故选:B.
4.解:∵△ABE≌△ACD,∠1=∠2,∠B=∠C,
∴AB=AC,∠BAE=∠CAD,BE=DC,AD=AE,
故A、B、C正确;
AD的对应边是AE而非DE,所以D错误.
故选:D.
5.解:∵△ABC≌△AED,
∴∠AED=∠B,AE=AB,∠BAC=∠EAD,
∴∠1=∠BAE=40°,
∴△ABE中,∠B==70°,
∴∠AED=70°,
故选:A.
6.解:如图,在△ABC和△DEA中,
,
∴△ABC≌△DEA(SAS),
∴∠1=∠4,
∵∠3+∠4=90°,
∴∠1+∠3=90°,
又∵∠2=45°,
∴∠1+∠2+∠3=90°+45°=135°.
故选:B.
7.解:∵△ABC≌△CDA,BC=DA
∴AB=CD,∠1=∠2,AC=CA,∠B=∠D,
∴A,B,D是正确的,C、AB=AD是错误的.
故选:C.
8.解:∵△ABC≌△CDE,AB=CD
∴∠ACB=∠CED,AC=CE,∠BAC=∠ECD,∠B=∠D
∴第三个选项∠ACB=∠ECD是错的.
故选:C.
9.解:∵∠B=80°,∠C=30°,
∴∠BAC=180°﹣80°﹣30°=70°,
∵△ABC≌△ADE,
∴∠DAE=∠BAC=70°,
∴∠EAC=∠DAE﹣∠DAC,
=70°﹣35°,
=35°.
故选:B.
10.解:∵,△ABC≌△EDC.
∴∠DCE=∠ACB=20°,∠BCD=∠ACE=90°,AC=CE,
∴∠ACD=90°﹣20°=70°,
∵点A,D,E在同一条直线上,
∴∠ADC+∠EDC=180°,
∵∠EDC+∠E+∠DCE=180°,
∴∠ADC=∠E+20°,
∵∠ACE=90°,AC=CE
∴∠DAC+∠E=90°,∠E=∠DAC=45°
在△ADC中,∠ADC+∠DAC+∠DCA=180°,
即45°+70°+∠ADC=180°,
解得:∠ADC=65°,
故选:C.
二.填空题
11.解:∵△ABC≌△ADE,
∴AE=AC,
∵AB=7,AC=3,
∴BE=AB﹣AE=AB﹣AC=7﹣3=4.
故答案为:4.
12.解:∵这两个三角形全等,两个三角形中都有2
∴长度为2的是对应边,x应是另一个三角形中的边6.同理可得y=5
∴x+y=11.
故答案为:11.
13.解:∵△ABC≌△DEF,
∴BC=EF
则EF=5.
故答案为:5.
14.解:∵△ABC≌△ADE,
∴AB=AD,∠BAC=∠DAE,
∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,
∴∠BAD=∠EAC,
∵∠EAC=40°,
∴∠BAD=40°,
∵AB=AD,
∴∠B=∠ADB=(180°﹣∠BAD)=70°,
故答案为:70°.
三.解答题
15.解:∵△ABC≌△ADE,
∴∠DAE=∠BAC=(∠EAB﹣∠CAD)=.
∴∠DFB=∠FAB+∠B=∠FAC+∠CAB+∠B=10°+55°+25°=90°
∠DGB=∠DFB﹣∠D=90°﹣25°=65°.
综上所述:∠DFB=90°,∠DGB=65°.
16.解:∵Rt△ABC≌Rt△DBF,∠ACB=∠DFB=90°,
∴BC=BF,BD=BA,
∴CD=AF,
在△DGC和△AGF中,
,
∴△DGC≌△AGF,
∴GC=GF,又∠ACB=∠DFB=90°,
∴∠CBG=∠FBG,
∴∠GBF=(90°﹣28°)÷2=31°.
17.解:(1)∵∠ABE=162°,∠DBC=30°,
∴∠ABD+∠CBE=132°,
∵△ABC≌△DBE,
∴∠ABC=∠DBE,
∴∠ABD=∠CBE=132°÷2=66°,
即∠CBE的度数为66°;
(2)∵△ABC≌△DBE,
∴DE=AC=AD+DC=5,BE=BC=4,
∴△CDP与△BEP的周长和=DC+DP+PC+BP+PE+BE=DC+DE+BC+BE=2.5+5+4+4=15.5.
18.证明:(1)∵△ABC≌△BAD,
∴∠CAB=∠DBA,
∴OA=OB.
(2)∵△ABC≌△BAD,
∴AC=BD,
又∵OA=OB,
∴AC﹣OA=BD﹣OB,
即:OC=OD,
∴∠OCD=∠ODC,
∵∠AOB=∠COD,∠CAB=,∠ACD=,
∴∠CAB=∠ACD,
∴AB∥CD.
19.解:(1)∵△EFG≌△NMH,∠F与∠M是对应角,
∴EF=NM,EG=NH,FG=MH,∠F=∠M,∠E=∠N,∠EGF=∠NHM,
∴FH=GM,∠EGM=∠NHF;
(2)∵EF=NM,EF=2.1cm,
∴MN=2.1cm;
∵FG=MH,FH+HG=FG,FH=1.1cm,HM=3.3cm,
∴HG=FG﹣FH=HM﹣FH=3.3﹣1.1=2.2cm.
20.证明:(1)∵△ABC≌△FED,
∴∠A=∠F.
∴AC∥DF.
(2)∵△ABC≌△FED,
∴AB=EF.
∴AB﹣EB=EF﹣EB.
∴AE=BF.
∵AF=8,BE=2
∴AE+BF=8﹣2=6
∴AE=3
∴AB=AE+BE=3+2=5
21.解:∵△OAD≌△OBC,
∴∠C=∠D,∠OBC=∠OAD,
∵∠0=65°,
∴∠OBC=180°﹣65°﹣∠C=115°﹣∠C,
在四边形AOBE中,∠O+∠OBC+∠BEA+∠OAD=360°,
∴65°+115°﹣∠C+135°+115°﹣∠C=360°,
解得∠C=35°.
22.解:(1)∵∠A=85°,∠B=60°,
∴∠ACB=180°﹣∠A﹣∠B=35°,
∵△ABC≌△DEF,AB=8,
∴∠F=∠ACB=35°,DE=AB=8,
∵EH=2,
∴DH=8﹣2=6;
(2)证明:∵△ABC≌△DEF,
∴∠DEF=∠B,
∴AB∥DE.
23.解:(1)其他对应角为:∠BAF和∠DCE,∠AFB和∠CED;
其他对应边为:AB和CD是对应边,BF和DE是对应边;
(2)∵△ABF≌△CDE,∠B=30°,
∴∠D=∠B=30°,
∵∠DCF=40°,
∴∠EFC=∠D+∠DCF=30°+40°=70°;
(3)∵△ABF≌△CDE,
∴BF=DE,
∴BF﹣EF=DE﹣EF,
∴DF=BE,
∵BD=10,EF=2,
∴DF=BE=4,
∴BF=BE+EF=4+2=6.
12.2
全等三角形
一、选择题
1.
如图,要用“SAS”证明△ABC≌△ADE,若已知AB=AD,AC=AE,则还需添加条件( )
A.∠B=∠D
B.∠C=∠E
C.∠1=∠2
D.∠3=∠4
2.
如图,已知∠1=∠2,欲证△ABD≌△ACD,还需从下列条件中补选一个,则错误的选项是( )
A.∠ADB=∠ADC
B.∠B=∠C
C.DB=DC
D.AB=AC
3.
(2019?临沂)如图,是上一点,交于点,,,若,,则的长是
A.0.5
B.1
C.1.5
D.2
4.
如图,点B,F,C,E在一条直线上,AB∥ED,AC∥FD,那么添加下列一个条件后,仍无法判定△ABC≌△DEF的是( )
A.AB=DE
B.AC=DF
C.∠A=∠D
D.BF=EC
5.
如图所示,在△ABC和△ABD中,∠C=∠D=90°,要利用“HL”判定Rt△ABC≌Rt△ABD成立,还需要添加的条件是
( )
A.∠BAC=∠BAD
B.BC=BD或AC=AD
C.∠ABC=∠ABD
D.AC=BD
6.
如图,BE⊥AC,CF⊥AB,垂足分别是E,F.若BE=CF,则图中全等三角形有( )
A.1对
B.2对
C.3对
D.4对
7.
如图,已知∠ABC=∠DCB,添加以下条件,不能判定△ABC≌△DCB的是( )
A.∠A=∠D
B.∠ACB=∠DBC
C.AC=DB
D.AB=DC
8.
如图,AB⊥CD,且AB=CD.E,F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
A.a+c
B.b+c
C.a-b+c
D.a+b-c
9.
观察图中的尺规作图痕迹,下列说法错误的是( )
A.∠DAE=∠EAC
B.∠C=∠EAC
C.AE∥BC
D.∠DAE=∠B
10.
如图,AB⊥BC,BE⊥AC,垂足分别为B,E,∠1=∠2,AD=AB,则下列结论正确的是( )
A.∠1=∠EFD
B.BE=EC
C.BF=CD
D.FD∥BC
二、填空题
11.
要测量河岸相对两点A,B之间的距离,已知AB垂直于河岸BF,先在BF上取两点C,D,使CD=CB,再过点D作BF的垂线段DE,使点A,C,E在一条直线上,如图,测出DE=20米,则AB的长是________米.
12.
如图K-10-10,CA=CD,AB=DE,BC=EC,AC与DE相交于点F,ED与AB相交于点G.若∠ACD=40°,则∠AGD=________°.
13.
如图,小明和小丽为了测量池塘两端A,B两点之间的距离,先取一个可以直接到达点A和点B的点C,沿AC方向走到点D处,使CD=AC;再用同样的方法确定点E,使CE=BC.若量得DE的长为60米,则池塘两端A,B两点之间的距离是______米.
14.
如图,在中,,以顶点为圆心,适当长度为半径画弧,分别交于点,再分别以点为圆心,大于的长为半径画弧,两弧交于点,作射线交于点.若,则__________.
15.
如图,在Rt△ABC中,∠ACB=90°,BC=2
cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F.若EF=5
cm,则AE=________cm.
三、解答题
16.
如图,AB=AD,BC=DC,点E在AC上.
求证:(1)AC平分∠BAD;
(2)BE=DE.
17.
已知:点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图①,若点O在边BC上,求证:AB=AC;
(2)如图②,若点O在△ABC的内部,求证:AB=AC;
(3)若点O在△ABC的外部,AB=AC成立吗?请画图表示.
图① 图②
18.
(2019?桂林)如图,,点在上.
(1)求证:平分;
(2)求证:.
19.
如图,点A,E,F,B在直线l上,AE=BF,AC∥BD,且AC=BD.求证:CF=DE.
20.
如图①,若AD=CD,AB=CB,则四边形ABCD是筝形.
(1)在同一平面内,△ABC与△ADE按图②所示的方式放置,其中∠B=∠D=90°,AB=AD,BC与DE相交于点F,请你判断四边形ABFD是不是筝形,并说明理由;
(2)请你结合图①,写出筝形的一个判定方法(定义除外):在四边形ABCD中,若________________,则四边形ABCD是筝形.
人教版
八年级数学
12.2
全等三角形
针对训练
-答案
一、选择题
1.
【答案】C [解析]
还需添加条件∠1=∠2.
理由:∵∠1=∠2,∴∠1+∠EAC=∠2+∠EAC,即∠BAC=∠DAE.
在△ABC和△ADE中,
∴△ABC≌△ADE(SAS).
2.
【答案】C [解析]
当添加条件A时,可用“ASA”证明△ABD≌△ACD;当添加条件B时,可用“AAS”证明△ABD≌△ACD;当添加条件D时,可用“SAS”证明△ABD≌△ACD;当添加条件C时,不能证明△ABD≌△ACD.
3.
【答案】B
【解析】∵,∴,,
在和中,,∴,∴,
∵,∴.故选B.
4.
【答案】C [解析]
选项A中添加AB=DE可用“AAS”进行判定,故本选项不符合题意;
选项B中添加AC=DF可用“AAS”进行判定,故本选项不符合题意;
选项C中添加∠A=∠D不能判定△ABC≌△DEF,故本选项符合题意;
选项D中添加BF=EC可得出BC=EF,然后可用“ASA”进行判定,故本选项不符合题意.
故选C.
5.
【答案】B [解析]
要添加的条件为BC=BD或AC=AD.理由:若添加的条件为BC=BD,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL);
若添加的条件为AC=AD,
在Rt△ABC和Rt△ABD中,
∴Rt△ABC≌Rt△ABD(HL).
6.
【答案】C [解析]
①∵BE⊥AC,CF⊥AB,
∴∠CFB=∠BEC=90°.
在Rt△BCF和Rt△CBE中,
∴Rt△BCF≌Rt△CBE(HL).
②∵BE⊥AC,CF⊥AB,∴∠AFC=∠AEB=90°.在△ABE和△ACF中,
∴△ABE≌△ACF(AAS).
③设BE与CF相交于点O.
∵BE⊥AC,CF⊥AB,
∴∠OFB=∠OEC=90°.
∵△ABE≌△ACF,∴AB=AC,AE=AF.
∴BF=CE.
在△BOF和△COE中,
∴△BOF≌△COE(AAS).
7.
【答案】C [解析]
A.∠A=∠D,∠ABC=∠DCB,BC=BC,符合“AAS”,即能推出△ABC≌△DCB,故本选项不符合题意;
B.∠ABC=∠DCB,BC=CB,∠ACB=∠DBC,符合“ASA”,即能推出△ABC≌△DCB,故本选项不符合题意;
C.∠ABC=∠DCB,AC=DB,BC=BC,不符合全等三角形的判定条件,即不能推出△ABC≌△DCB,故本选项符合题意;
D.AB=DC,∠ABC=∠DCB,BC=CB,符合“SAS”,即能推出△ABC≌△DCB,故本选项不符合题意.
故选C.
8.
【答案】D [解析]
∵AB⊥CD,CE⊥AD,BF⊥AD,∴∠CED=∠AFB=90°,∠A=∠C.又∵AB=CD,∴△CED≌△AFB.∴AF=CE=a,DE=BF=b,DF=DE-EF=b-c.∴AD=AF+DF=a+b-c.故选D.
9.
【答案】A [解析]
根据图中尺规作图的痕迹,可得∠DAE=∠B,故D选项正确,∴AE∥BC,故C选项正确.∴∠EAC=∠C,故B选项正确.
∵∠DAE=∠B,∠EAC=∠C,而∠C与∠B的大小关系不确定,所以∠DAE与∠EAC的大小关系不确定.故选A.
10.
【答案】D [解析]
在△AFD和△AFB中,
∴△AFD≌△AFB.
∴∠ADF=∠ABF.
∵AB⊥BC,BE⊥AC,
∴∠BEC=∠ABC=90°.
∴∠ABF+∠EBC=90°,∠C+∠EBC=90°.
∴∠ADF=∠ABF=∠C.
∴FD∥BC.
二、填空题
11.
【答案】20
12.
【答案】40 [解析]
在△ABC和△DEC中,
∴△ABC≌△DEC(SSS).
∴∠A=∠D.
又∵∠AFG=∠DFC,
∴∠AGD=∠ACD=40°.
13.
【答案】60 [解析]
在△ACB和△DCE中,
∴△ACB≌△DCE(SAS).∴DE=AB.
∵DE=60米,∴AB=60米.
14.
【答案】
【解析】由作法得平分,
∵,,∴,
∴,∴,
在中,,∴,
∴.故答案为:.
15.
【答案】3 [解析]
∵∠ACB=90°,∴∠ECF+∠BCD=90°.∵CD⊥AB,∴∠BCD+∠B=90°.
∴∠ECF=∠B.
在△ABC和△FCE中,
∴△ABC≌△FCE(ASA).∴AC=FE.
∵AE=AC-CE,BC=2
cm,EF=5
cm,
∴AE=5-2=3(cm).
三、解答题
16.
【答案】
证明:(1)在△ABC与△ADC中,
∴△ABC≌△ADC(SSS).
∴∠BAC=∠DAC,
即AC平分∠BAD.
(2)由(1)知∠BAE=∠DAE.
在△BAE与△DAE中,
∴△BAE≌△DAE(SAS).
∴BE=DE.
17.
【答案】
(1)证明:如图①,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF,OB=OC,
解图①
∴Rt△OEB≌Rt△OFC,
∴∠B=∠C,从而AB=AC.
(2)证明:如图②,过点O分别作OE⊥AB,OF⊥AC,E、F分别是垂足,由题意知,OE=OF.
在Rt△OEB和Rt△OFC中,
∵OE=OF,OB=OC,
解图②
∴Rt△OEB≌Rt△OFC.
∴∠OBE=∠OCF,
又由OB=OC知∠OBC=∠OCB,
∴∠ABC=∠ACB.
∴AB=AC.
(3)解:不一定成立.
(注:当∠A的平分线所在直线与边BC的垂直平分线重合时,有AB=AC;否则,AB≠AC,如示例图③)
解图③
18.
【答案】
(1)在与中,,
∴,
∴,
即平分.
(2)由(1),
在与中,得,
∴,
∴.
19.
【答案】
证明:∵AE=BF,∴AE+EF=BF+EF,
即AF=BE.
∵AC∥BD,∴∠CAF=∠DBE.
在△ACF和△BDE中,
∴△ACF≌△BDE(SAS).
∴CF=DE.
20.
【答案】
解:(1)四边形ABFD是筝形.
理由:连接AF.
在Rt△AFB和Rt△AFD中,
∴Rt△AFB≌Rt△AFD(HL).∴BF=DF.
又∵AB=AD,∴四边形ABFD是筝形.
(2)答案不唯一,如AD=CD,∠ADB=∠CDB
12.3角平分线的性质
一.选择题
1.已知:在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于D,若BC=20,且BD:DC=3:2,则点D到AB边的距离为( )
A.8
B.12
C.10
D.15
2.如图已知OC平分∠AOB,P是距离是OC上一点,PH⊥OB于点H,若PH=5,则点
P到射线OA的距离是( )
A.6
B.5
C.4
D.3
3.如图,四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=8,BD=13,BC=12,则四边形ABCD的面积为( )
A.30
B.40
C.50
D.60
4.如图,在△ABC中,BD是AC边上的高,AE平分∠CAB,交BD于点E,AB=8,DE=3,则△ABE的面积等于( )
A.15
B.12
C.10
D.14
5.如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,∠CAB和∠ABC的平分线交于点O,OM⊥BC于点M,则OM的长为( )
A.1
B.2
C.3
D.4
6.如图,四边形ABCD中,∠A=90°,AD=2,连接BD,BD⊥CD,垂足是D且∠ADB=∠C,点P是边BC上的一动点,则DP的最小值是( )
A.1
B.1.5
C.2
D.2.5
7.如图,AD∥BC,BG,AG分别平分∠ABC与∠BAD,GH⊥AB,GH=5,则AD与BC之间的距离是( )
A.5
B.8
C.10
D.15
8.下列关于几何画图的语句,正确的是( )
A.延长射线AB到点C,使BC=2AB
B.点P在线段AB上,点Q在直线AB的反向延长线上
C.将射线OA绕点O旋转,当终止位置OB与起始位置OA成一条直线时形成平角
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b
9.如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M,N,再分别以点M,N为圆心,大于MN的长为半径画弧,两弧交于点P,作射线AP交边BC于点D,若CD=5,AB=12,则△ABD的面积是( )
A.15
B.30
C.45
D.60
10.如图,点M在线段BC上,点E和N在线段AC上,EM∥AB,BE和MN分别平分∠ABC和∠EMC.下列结论中不正确的是( )
A.∠MBE=∠MEB
B.MN∥BE
C.S△BEM=S△BEN
D.∠MBN=∠MNB
二.填空题
11.如图,在△ABC中,∠ACB=90°,AD是△ABC的角平分线,BC=5cm,BD:DC=3:2,则点D到AB的距离为
.
12.如图点D是△ABC的两外角平分线的交点,下列说法:
①AD=CD;
②AB=AC;
③D到AB、BC所在直线的距离相等;
@点D在∠B的平分线上;
其中正确的说法的序号是
.
13.已知如图,OP平分∠MON,PA⊥ON于点A,PA=4,点Q是射线OM上的一个动点,则线段PQ的最小值是
.
14.在正方形网格中,∠AOB的位置如图所示,则点P、Q、M、N中在∠AOB的平分线上是
点.
15.如图,已知△ABC的周长是16.MB和MC分别平分∠ABC和∠ACB.过点M作BC的垂线交BC于点D,且MD=4.则△ABC的面积是
.
三.解答题
16.如图,直线AC分别与射线DE交于A,与射线BF交于C,连接AB,连接DC,∠1+∠2=180°,AD=BC.若DC平分∠ACF,证明AB平分∠EAC.
17.如图,三角形ABC中,点D在AC上.
(1)请你过点D做DE平行BC,交AB于E.如果点E在∠C的平分线上,∠C=44°,那么∠DEC=
.
18.已知:在△ABC中,∠ABC=60°,∠ACB=40°,BD平分∠ABC,CD平分∠ACB,
(1)如图1,求∠BDC的度数;
(2)如图2,连接AD,作DE⊥AB,DE=2,AC=4,求△ADC的面积.
19.在△ABC中,∠ABC和∠ACB的平分线相交于点O,
(1)若∠ABC=60°,∠ACB=40°,求∠BOC的度数;
(2)若∠ABC=60°,OB=4,且△ABC的周长为16,求△ABC的面积.
参考答案与试题解析
一.选择题
1.【解答】解:∵BC=20,BD:DC=3:2,
∴CD=8,
∵∠C=90°
AD平分∠BAC
∴D到边AB的距离=CD=8.
故选:A.
2.【解答】解:作PQ⊥OA于Q,如图,
∵OC为∠AOB的平分线,PH⊥OB,PQ⊥OA,
∴PQ=PH=5,
即点P到射线OA的距离为5.
故选:B.
3.【解答】解:
过D作DE⊥AB,交BA的延长线于E,则∠E=∠C=90°,
∵∠BCD=90°,BD平分∠ABC,
∴DE=DC,
在Rt△BCD中,由勾股定理得:CD===5,
∴DE=5,
在Rt△BED中,由勾股定理得:BE===12,
∵AB=8,
∴AE=BE﹣AB=12﹣8=4,
∴四边形ABCD的面积S=S△BCD+S△BED﹣S△AED
=+﹣
=+﹣
=50,
故选:C.
4.【解答】解:过点E作EF⊥AB于点F,如图:
∵BD是AC边上的高,
∴ED⊥AC,
又∵AE平分∠CAB,DE=3,
∴EF=3,
∵AB=8,
∴△ABE的面积为:8×3÷2=12.
故选:B.
5.【解答】解:过O作OD⊥AC于D,OE⊥AB于E,
∵AO平分∠CAB,OB平分∠ABC,
∴OD=OE=OM,
∵在Rt△ABC中,∠C=90°,AC=8,BC=6,AB=10,
∴S△ABC=ACBC=×ABOE+ACOD+BCOM,
∴=+OM+,
∴OM=2,
故选:B.
6.【解答】解:过点D作DE⊥BC于E,则DE即为DP的最小值,
∵∠BAD=∠BDC=90°,∠ADB=∠C,
∴∠ABD=∠CBD,
∵∠ABD=∠CBD,DA⊥AB,DE⊥BC,
∴DE=AD=2,
故选:C.
7.【解答】解:作GE⊥AD于E,EG的延长线交BC于F,如图,则∠DEG=90°,
∵AD∥BC,
∴∠BFG=∠DEG=90°,
∴EF⊥BC,
∵BG,AG分别平分∠ABC与∠BAD,
∴GE=GH=5,GF=GH=5,
∴EF=5+5=10,
即AD与BC之间的距离为10.
故选:C.
8.【解答】解:A.延长射线AB到点C,使BC=2AB,
因为射线不能延长,
所以A选项错误,不符合题意;
B.因为直线不能反向延长,
所以B选项错误,不符合题意;
C.将射线OA绕点O旋转,当终止位置OB与起始位置OA成一条直线时形成平角.
C选项正确,符号题意;
D.已知线段a、b,若在同一直线上作线段AB=a,BC=b,则线段AC=a+b或=a﹣b.
所以D选项错误,不符合题意.
故选:C.
9.【解答】解:作DE⊥AB于E,
由基本尺规作图可知,AD是△ABC的角平分线,
∵∠C=90°,
∴DC⊥AC,
∵DE⊥AB,DC⊥AC,
∴DE=DC=5,
∴△ABD的面积=×AB×DE=×12×5=30,
故选:B.
10.【解答】解:∵EM∥AB,BE和MN分别平分∠ABC和∠EMC,
∴∠MEB=∠ABE,∠ABC=∠EMC,∠ABE=∠MBE,∠EMN=∠NMC,
∴∠MEB=∠MBE(故A正确),∠EBM=∠NMC,
∴MN∥BE(故B正确),
∴MN和BE之间的距离处处相等,
∴S△BEM=S△BEN(故C正确),
∵∠MNB=∠EBN,而∠EBN和∠MBN的关系不知,
∴∠MBN和∠MNB的关系无法确定,故D错误,
故选:D.
二.填空题
11.【解答】解:作DE⊥AB于E,如图,
∵BC=5cm,BD:DC=3:2,
∴BD=3,CD=2,
∵AD是△ABC的角平分线,
∴DC=DE=2,
即点D到AB的距离为2.
故答案为2.
12.【解答】解:AD与CD不能确定相等,AB与AC也不能确定相等,所以①②错误;
作DE⊥BA于E,DF⊥BC于F,DH⊥AC于H,如图,
∵AD平分∠EAC,
∴DE=DH,
同理可得DH=DF,
∴DE=DF,
即D到AB、BC所在直线的距离相等,所以③正确;
∴点D在∠B的平分线上;所以④正确.
故答案为③④.
13.【解答】解:当PQ⊥OM时,PQ有最小值.
∵OP平分∠MON,PA⊥ON于点A,PA=4,
∴PQ=PA=4,
故答案为4.
14.【解答】解:点P、Q、M、N中在∠AOB的平分线上是Q点.
故答案为Q.
15.【解答】解:连接AM,过M作ME于E,MF⊥AC于F,
∵MD⊥BC,MB和MC分别平分∠ABC和∠ACB,MD=4,
∴ME=MD=4,MF=MD=4,
∵△ABC的周长是16,
∴AB+BC+AC=16,
∴△ABC的面积S=S△ABM+S△BCM+S△ACM
=+
=
=2AB+2BC+2AC
=2(AB+BC+AC)
=2×16
=32,
故答案为:32.
三.解答题
16.【解答】证明:∠1+∠2=180°,∠1+∠ACB=180°,
∴∠2=∠ACB,
∴AD∥BC,
又∵AD=BC,
∴四边形ABCD为平行四边形,
∴DC∥AB,
∴∠DCF=∠B,∠DCA=∠BAC,
∵DC平分∠ACF,
∴∠DCF=∠DCA,
∴∠B=∠BAC,
∵AD∥BC,
∴∠EAB=∠B,
∴∠BAC=∠EAB,即AB平分∠EAC.
17.【解答】解:(1)如图1所示:
作∠ADE=∠C交AB于E,DE即为所求;
(2)如图2所示:
∵DE∥BC,
∴∠DEC=∠BCE,
∵EC平分∠ACB,
∴∠DCE=∠BCE,
∴∠DEC=∠DCE,
∴DC=DE,
∴△DEC是等腰三角形,
∴∠DEC=∠C=22°;
故答案为:22°.
18.【解答】解:(1)∵BD平分∠ABC,
∴∠DBC=∠ABC=×60°=30°,
∵CD平分∠ACB,
∴∠DCB=∠ACB=×40°=20°,
∴∠BDC=180°﹣∠DBC﹣∠DCB
=180°﹣30°﹣20°
=130°;
(2)作DF⊥AC于F,DH⊥BC于H,如图2,
∵BD平分∠ABC,DE⊥AB,DH⊥BC,
∴DH=DE=2,
∵CD平分∠ACB,DF⊥AC,DH⊥BC,
∴DF=DH=2,
∴△ADC的面积=DFAC=×2×4=4.
19.【解答】解:(1)∵BO、CO分别平分∠ABC和∠ACB,
∵∠ABC=60°,∠ACB=40°
∴∠OBC=30°,∠OCB=20°,
∴∠COB=180°﹣(30°+20°)=130°;
(2)过O作OD⊥AB于D点,OE⊥AC于E,OF⊥BC于F,连接AO,如图,
∵∠ABC=60°,OB=4
∴∠OBD=30°,
∴OD=OB=2,
∵∠ABC和∠ACB的平分线相交于点O,
∴OE=OF=2,
∵S△ABC=S△AOB+S△AOC+S△BOC
=×2×AB+×2×AC+×2×B
