人教版_选修1-1_二、电场课件41张PPT
文档属性
| 名称 | 人教版_选修1-1_二、电场课件41张PPT |

|
|
| 格式 | ppt | ||
| 文件大小 | 694.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2020-12-15 22:45:29 | ||
图片预览










文档简介
单击此处编辑母版标题样式
单击此处编辑母版副标题样式
*
*
*
学案 电 场
知识回顾
1.库仑定律:真空中两个静止点电荷之间的相互作用,与它们的电荷量的乘积成 ,与它们的距离的二次方成反比,作用力的方向在 .即:F=k ,其中k为静电力常量,大小为9.0×
109 N·m2/C2.
成立条件:① (空气中也近似成立);
正比
它们的连线上
真空中
② ——即带电体的形状和大小对相互作用力的影响可以忽略不计.对带电导体球,距离近了以后,电荷会重新分布,不能再用球心间距代替r.
点电荷
2.电场的最基本的性质是对放入其中的电荷 .电场强度E是描述电场的力的性质的物理量.
3.对电场强度的三个公式的理解
(1)E= 是电场强度的 式,适用于 电场.电场中某点的场强是确定值,其大小和方向与试探电荷q无关.试探电荷q充当“测量工具”的作用.
有力的
作用
定义
任何
(2)E=k 是真空中点电荷所形成的电场的决定式.E由场源电荷Q和场源电荷到某点的距离r决定.
(3)E= 是场强与电势差的关系式,只适用于 ,注意式中d为两点间沿电场方向的距离.
4.电势:φA=UAO=φA-φO= (其中φO=0),可由等势面形象描绘.
电势高低的判别:
(1)电场线法,顺着电场线电势越来越 ;
(2)电场力做功法,正电荷仅在电场力作用下移动,电场力做 功,电荷由 处移向 处;
匀强
电场
低
正
高电势
低电势
(3)电势能法,正电荷在高电势处电势能 ,负电荷在低电势处电势能 .
5.电势差: ,UAB、WAB、q都有正负号,但含义不同,UAB的正负反映了A、B两点电势的高低;WAB的正负反映了是电场力做正功还是克服电场力做功;q的正负反映电荷的电性.
6.电势能: .
电势能大小的比较:
(1)做功法:电场力做正功,电势能减小;克服电场力做功,电势能增加.即 .
大
大
UAB= =φA-φB
Ep=qφ
W电场=Ep1-Ep2=-ΔEp
(2)电场线法:正电荷顺着电场线移动,电势能越来越小;负电荷顺着电场线移动,电势能越来越大.
(3)正电荷:电势能的正负跟电势的正负相同;
负电荷:电势能的正负跟电势的正负相反.
方法点拨
带电粒子在匀强电场中的运动
1.加速——带电粒子的受力与运动方向共线.
处理方法:
(1)牛顿定律和运动学方程相结合.
(2)功能关系: .
qU= mv22- mv12
2.偏转——带电粒子以初速度v0垂直于电场线方向进入匀强电场.
处理方法:类似平抛运动的分析方法.
沿初速度方向的匀速直线运动:x= ,沿电场力方向的初速度为零的匀加速直线运动:y= = · ·t2
偏转角tan θ= = .
v0t
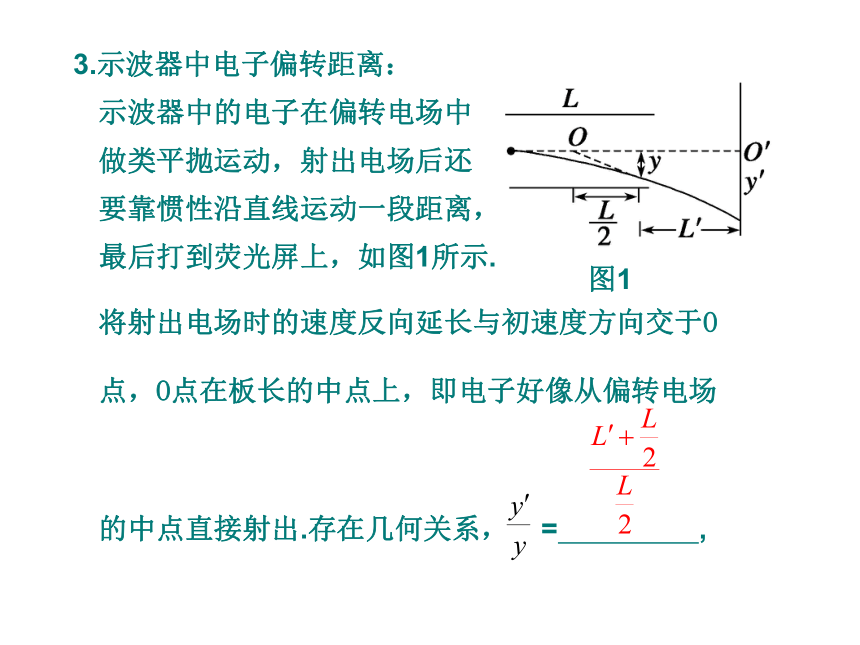
3.示波器中电子偏转距离:
示波器中的电子在偏转电场中
做类平抛运动,射出电场后还
要靠惯性沿直线运动一段距离,
最后打到荧光屏上,如图1所示.
将射出电场时的速度反向延长与初速度方向交于O点,O点在板长的中点上,即电子好像从偏转电场
的中点直接射出.存在几何关系, = ,
图1
得y′= ,又y= at2= ,L=v0t
所以,y′= .
注意 是否需要考虑带电体的重力?
(1)基本粒子:如电子、α粒子、离子等,除有说明或暗示以外,一般都不考虑重力.
(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或暗示以外,一般都需要考虑重力.
类型一 电场的基本性质
例1 (2009·全国卷Ⅰ·18)如图2所示,
一电场的电场线分布关于y轴(沿竖直
方向)对称,O、M、N是y轴上的三个
点,且OM=MN.P点在y轴右侧,MP⊥
ON.则 ( )
A.M点的电势比P点的电势高
B.将负电荷由O点移动到P点,电场力做正功
C.M、N两点间的电势差大于O、M两点间的电势差
D.在O点静止释放一带正电粒子,该粒子将沿y轴
做直线运动
图2
解析 根据等势线与电场线的关系,分别作出过M点和P点的等势线,M与P不在一条等势线上,因沿电场线方向电势降低,所以M点的电势高于P点的电势,即选项A正确.O点电势高于P点电势,移动负电荷由O点移动到P点,电场力做负功,故选项B错误.从O到N电场线越来越稀,表明从O到N电场强度越来越小,而OM=MN,所以M、N两点间的电势差低于O、M两点间的电势差,故C选项错误.沿y轴的电场强度的方向沿y轴的正方向,从O点释放一静止的带正电粒子,所受电场力的方向沿y轴正方向,因此带电粒子将沿y轴正方向做直线运动,故D对.
答案 AD
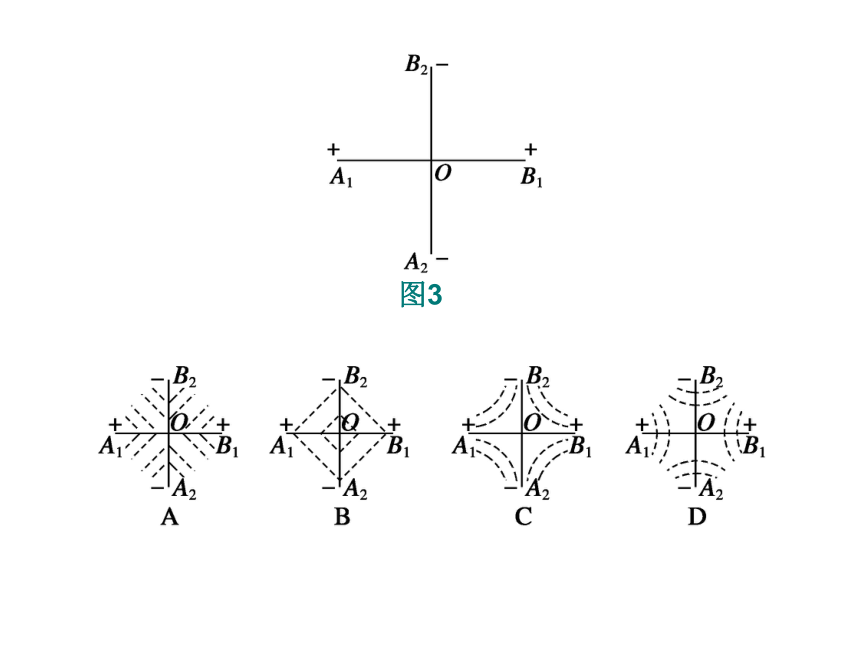
预测1 研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场.现有两块无限大的均匀绝缘带电平面,一块带正电,一块带负电,把它们放置(如图3)所示,单位面积所带电荷的数值相等.图3中直线A1B1和A2B2分别为带正电和带负电的平面与纸面正交的交线,O为两交线的交点,两平面间绝缘,则下面四个选项中能正确反映等势面分布情况的是 ( )
图3
解析 带正电的平面A1B1在平面上方产生的匀强电场方向向上,在平面下方产生的匀强电场方向向下;带负电的平面A2B2在平面左边产生的电场方向向右,在平面右边产生的电场方向向左;空间电场为两电场的矢量和,在各象限内的电场如图所示,由电场线与等势面处垂直可知,A图正确.
答案 A
解题归纳 电场的描述一般从两个方面展开:
(1)力的性质E= ;(2)能的性质φ=
类型二 带电粒子在电场中的加速和偏转
例2 如图4所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界是边长为L的正方形(不计电子所受重力).
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置;
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置;
(3)若将左侧电场Ⅱ整体水平向右移动L/n(n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场Ⅰ区域内由静止释放电子的所有位置.
图4
解析 (1)设电子的质量为m,电量为e,电子在电场Ⅰ中做匀加速直线运动,出区域Ⅰ时的速度为v0,此后在电场Ⅱ内做类平抛运动,假设电子从CD边射出,出射点的纵坐标为y,有eEL= mv02; -y
= at2=
解得y= L,所以原假设成立,即电子离开ABCD区域的位置坐标为(-2L, L)
(2)设释放点在电场区域Ⅰ中,其坐标为(x,y),在电场Ⅰ中电子被加速到v1,然后进入电场Ⅱ做类平抛运动,并从D点离开,有
eEx= mv12
y= at2=
解得xy= ,即在电场Ⅰ区域内满足方程的点即为所求位置.
(3)设电子从(x,y)点释放,在电场Ⅰ中加速到v2,进入电场Ⅱ后做类平抛运动,在高度为y′处离开电场Ⅱ时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有
eEx= mv22
y-y′= at2=
vy=at= ,y′=vy
解得xy=L2 ,即在电场Ⅰ区域内满足方程的点即为所求位置.
答案 (1)(-2L, )(2)xy=
(3)xy=
解题归纳 本题考查了考生对牛顿第二定律、动能定理、运动学基本规律、平抛运动及其分析处理方法的理解.着重考查了考生的理解能力、推理能力和分析综合能力,题目难度较大,搞清楚带电粒子在不同过程的衔接点即中间转折状态是解题的关键.
预测2 静电喷漆技术具有效率高,浪
费少,质量好,有利于工人健康等
优点,其装置如图5所示.A、B为两
块平行金属板,间距d=0.40 m,两板
间有方向由B指向A,大小为E=1.0×103 N/C的匀强电场.在A板中央放置一个安全接地的静电油漆喷枪P,油漆喷呛的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的初速度大小均为v0=2.0 m/s,质量m=5.0×10-15 kg,电荷量为q=-2.0×10-16C.微粒的重力和所受空气阻力均不计,油漆微粒最后都落在金属板B上.试求:
图5
(1)电场力对每个微粒所做的功;
(2)微粒打在B板上的速度;
(3)微粒最后落在B板上所形成的图形及其面积的大小.
解析 (1)由电场力做功可知W=qEd=8.0×10-14J.
(2)由动能定理可得W= mv2- mv02,得v=6.0 m/s.
(3)微粒最后落在B板上所形成的图形为圆形
微粒运动的加速度a= ,而d= at12,R=v0t1,所以圆的面积S=πR2,综合以上各式并代入数据可得
S=0.25 m2.
答案 (1)8.0×10-14J (2)6.0 m/s (3)圆形0.25 m2
解题归纳 忽略带电粒子的重力和空气阻力,速度方向沿竖直方向的粒子的运动为类平抛运动,研究的方法和平抛运动类似,但要注意克服思维定势,要具体分析物体的初速度方向和受力方向,不要总认为水平方向匀速,竖直方向匀变速.还要注意类平抛运动和平抛运动的区别:所有平抛运动的加速度都是重力加速度,而带电粒子的类平抛运动的加速度a= ,
要具体问题具体分析,并且加速度可能会随着两板间距离的变化、电势差的变化而变化.
类型三 带电粒子在交变电场中的运动
例3 如图6甲所示,水平放置的平行金属板A和B的距离为d,它们的右端安放着垂直于金属板的靶MN,现在A、B板上加上如图乙所示的方波电压,电压的正向值为U0,反向电压值U0/2,且每隔T/2换向一次.现有质量为m、带正电且电荷量为q的粒子组成的粒子束从A、B的中点O沿平行于金属板方向OO′射入,设粒子能全部打在靶上且所有粒子在A、B间的飞行时间均为T.不计重力的影响,试求在靶MN上距其中心O′点多远的范围内有粒子击中?
图6
解析 若粒子在正向电压开始射入平行金属板A、B间.在前T/2时间内,粒子向下偏转,粒子沿电场方向的加速度大小a1=
竖直位移x1= a1t2=
T/2末的竖直分速度v1=a1·
在后T/2时间内,粒子沿电场方向的加速度大小
a2=
竖直位移x2=v1
粒子打在O′点正下方的最大位移为x=x1+x2=
若粒子在反向电压开始时射入平行金属板A、B间.在前T/2时间内,粒子向上偏转,粒子沿电场方向的加速度大小a1′=
T/2末的竖直分速度v1′=a1′·
竖直位移x1′= a1′t2=
在后T/2时间内,粒子沿电场方向的加速度大小
a2′=
竖直位移x2′=v1′T/2- a2′t2= · · -
· =0
粒子打在O′点正上方的最大位移为x′=x1′+x2′=
所以,在靶MN上O′点正上方 处与O′点正下方 处之间的范围内有粒子击中.
答案 见解析
类型四 电场综合应用
例4 如图7甲所示,在场强大小为E、方向竖直向下的匀强电场内存在一个半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最高点,B点是圆形区域最右侧的点.在A点由放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电荷量为q,不计电荷的重力.
图7
(1)正电荷以多大的速率发射,才能经过图中的P点(图甲中∠POA′=θ为已知)?
(2)在问题(1)中,正电荷经过P点的动能是多大?
(3)若在圆形区域的边缘有一接收屏CBD,其中C、D分别为接收屏上最边缘的两点(如图乙所示),且∠COB=∠BOD=30?;则该屏上接收到的正电荷的最大动能是多少?
解析 (1)正电荷做类平抛运动,则
a= ①
Rsin θ=v0t ②
R+Rcos θ= at2 ③
由以上三式解得v0= ④
(2)由④式可得正电荷从A点出发时的动能为
Ek0= mv02= ,则经过P点时的动能为Ek=qE(R+Rcos θ)+ mv02= qER(5+3cos θ) ⑤
(3)从⑤式可以看出,当θ从0?到180?变化过程中,接收屏上正电荷的动能逐渐减小,即θ越小接收的正电荷动能越大,因此D点接收到的正电荷的末动能最大.最大动能为:
EkD= qER(5+3 cos 60?)= qER.
答案 (1)
(2) qER(5+3cos θ)
(3) qER
解题归纳 正电荷在电场中受到电场力作用,电场力与初速度方向垂直且恒定,因此正电荷做类平抛运动,用正交分解法分析即可确定经过P点正电荷的初速度,再由动能定理即可求出正电荷经过P点时的动能;正电荷的动能是一个关于角θ的函数,利用数学方法可求出CBD屏上接收到的正电荷的动能的最大值.
1.(2009·徐州模拟)如图所示的真空空间中,仅在正方体中的黑点处存在着电荷量大小相等的点电荷,则图中a、b两点电场强度和电势均相同的是 ( )
解析 根据场强叠加的矢量性,及等量异种电荷、等量同种电荷中线上场强分析规律可判断C选项正确.
C
2. (2009·大连模拟)如图8所示,三个同心圆是点电荷Q周围的三个等势面,已知这三个圆的半径成等差数列,A、B、C分别是这三个等势面上的点,且这三点在同一条电场线上.将电量为q=+1.6×10-6C的电荷从A点移到C点,电势能减少1.92×10-5J,若取C点为电势零点(φ=0),则B点的电势是( )
A.一定等于6 V B.一定低于6 V
C.一定高于6 V D.无法确定
图8
解析 UAC= =12 V
由于从A→C场强逐渐减小,所以UAB>UBC.若选φC=0,则φB<6 V.
答案 B
3.(2009·上海质检)研究发现,某类微观带电粒子
之间的相互作用力F与它们之间的距离r的关系为:
式中F0为大于零的常量,负号表示引力.用U表示这类微观带电粒子间的势能,令U0=F0(r2-r1),取无穷远为势能零点,下列U-r图象正确的是 ( )
解析 当r>r2时,F=0,电场力不做功,电势能不变,即为0;当r1≤r≤r2时,电场力为-F0,所以从r2→r1电势能减小;当rB
4.(2009·海南卷·10)如图9所示,
两等量异号的点电荷相距为a.M
与两点电荷共线,N位于两点电
荷连线的中垂线上,两点电荷连
线中点到M和N的距离都为L,且
L?a.略去(a/L)n(n≥2) 项的
贡献,则两点电荷的合电场在M和N点的强度
( )
A.大小之比为2,方向相反
B.大小之比为1,方向相反
C.大小均与a成正比,方向相反
D.大小均与L的平方成反比,方向相互垂直
图9
解析 如下图所示,合电场在M和N点的强度分别为
E1= ,E2= ,E1∶E2=2;又N点处强场方向由+q指向-q,在M点的场强表现+q的点电荷、由-q指向+q.
答案 AC
5. (2009·上海虹口区)如图10所示,
一竖直固定且光滑绝缘的直圆筒底
部放置一可视为点电荷的 场源电荷
A,其电荷量Q=+4×10-3C,场源电
荷A形成的电场中各点的电势表达式
为φ= ,其中k为静电力恒量,r
为空间某点到A的距离.现有一个质量
为m=0.1 kg的带正电的小球B,它与A球间的距离为a=0.4 m,此时小球B处于平衡状态,且小球B在场源电荷A形成的电场中具有电势能表达式为?= ,其中r为q与Q之间的距离.另一质量也为m的
图10
不带电绝缘小球C从距离B的上方H=0.8 m处自由下
落,落在小球B上立刻与小球B粘在一起以2 m/s向
下运动,它们到达最低点后又向上运动,向上运动
到达的最高点为P0(取g=10 m/s2,k=9×109 N·m2/C2),
求:
(1)小球C与小球B碰撞前的速度大小v0为多少?
(2)小球B的带电量q为多少?
(3)P点与小球A之间的距离为多大?
(4)当小球B和C一起向下运动与场源电荷A距离多远时,其速度最大?速度的最大值为多少?
解析 (1)小球C自由下落H距离的速度
v0= =4 m/s
(2)小球B在碰撞前处于平衡状态,对B球进行受力分析知:mg=k
代入数据得q = ×10-8C
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒,设P与A之间的距离为x,由能量守恒得
代入数据得x=0.68 m或x=(0.4+ )m
(4)当C和B向下运动的速度最大时,与A之间的距离为y,对C和B整体受力分析有:2mg=k ,
代入数据有y=0.28 m(或y= m)
由能量守恒得
·2mv2+k = ·2mvm2-2mg(a-y)+k
代入数据得vm=2.16 m/s(或vm= m/s)
答案 (1)4 m/s (2) ×10-8C (3)0.68 m
(4)0.28 m 2.16 m/s
返回
单击此处编辑母版副标题样式
*
*
*
学案 电 场
知识回顾
1.库仑定律:真空中两个静止点电荷之间的相互作用,与它们的电荷量的乘积成 ,与它们的距离的二次方成反比,作用力的方向在 .即:F=k ,其中k为静电力常量,大小为9.0×
109 N·m2/C2.
成立条件:① (空气中也近似成立);
正比
它们的连线上
真空中
② ——即带电体的形状和大小对相互作用力的影响可以忽略不计.对带电导体球,距离近了以后,电荷会重新分布,不能再用球心间距代替r.
点电荷
2.电场的最基本的性质是对放入其中的电荷 .电场强度E是描述电场的力的性质的物理量.
3.对电场强度的三个公式的理解
(1)E= 是电场强度的 式,适用于 电场.电场中某点的场强是确定值,其大小和方向与试探电荷q无关.试探电荷q充当“测量工具”的作用.
有力的
作用
定义
任何
(2)E=k 是真空中点电荷所形成的电场的决定式.E由场源电荷Q和场源电荷到某点的距离r决定.
(3)E= 是场强与电势差的关系式,只适用于 ,注意式中d为两点间沿电场方向的距离.
4.电势:φA=UAO=φA-φO= (其中φO=0),可由等势面形象描绘.
电势高低的判别:
(1)电场线法,顺着电场线电势越来越 ;
(2)电场力做功法,正电荷仅在电场力作用下移动,电场力做 功,电荷由 处移向 处;
匀强
电场
低
正
高电势
低电势
(3)电势能法,正电荷在高电势处电势能 ,负电荷在低电势处电势能 .
5.电势差: ,UAB、WAB、q都有正负号,但含义不同,UAB的正负反映了A、B两点电势的高低;WAB的正负反映了是电场力做正功还是克服电场力做功;q的正负反映电荷的电性.
6.电势能: .
电势能大小的比较:
(1)做功法:电场力做正功,电势能减小;克服电场力做功,电势能增加.即 .
大
大
UAB= =φA-φB
Ep=qφ
W电场=Ep1-Ep2=-ΔEp
(2)电场线法:正电荷顺着电场线移动,电势能越来越小;负电荷顺着电场线移动,电势能越来越大.
(3)正电荷:电势能的正负跟电势的正负相同;
负电荷:电势能的正负跟电势的正负相反.
方法点拨
带电粒子在匀强电场中的运动
1.加速——带电粒子的受力与运动方向共线.
处理方法:
(1)牛顿定律和运动学方程相结合.
(2)功能关系: .
qU= mv22- mv12
2.偏转——带电粒子以初速度v0垂直于电场线方向进入匀强电场.
处理方法:类似平抛运动的分析方法.
沿初速度方向的匀速直线运动:x= ,沿电场力方向的初速度为零的匀加速直线运动:y= = · ·t2
偏转角tan θ= = .
v0t
3.示波器中电子偏转距离:
示波器中的电子在偏转电场中
做类平抛运动,射出电场后还
要靠惯性沿直线运动一段距离,
最后打到荧光屏上,如图1所示.
将射出电场时的速度反向延长与初速度方向交于O点,O点在板长的中点上,即电子好像从偏转电场
的中点直接射出.存在几何关系, = ,
图1
得y′= ,又y= at2= ,L=v0t
所以,y′= .
注意 是否需要考虑带电体的重力?
(1)基本粒子:如电子、α粒子、离子等,除有说明或暗示以外,一般都不考虑重力.
(2)带电颗粒:如液滴、油滴、尘埃、小球等,除有说明或暗示以外,一般都需要考虑重力.
类型一 电场的基本性质
例1 (2009·全国卷Ⅰ·18)如图2所示,
一电场的电场线分布关于y轴(沿竖直
方向)对称,O、M、N是y轴上的三个
点,且OM=MN.P点在y轴右侧,MP⊥
ON.则 ( )
A.M点的电势比P点的电势高
B.将负电荷由O点移动到P点,电场力做正功
C.M、N两点间的电势差大于O、M两点间的电势差
D.在O点静止释放一带正电粒子,该粒子将沿y轴
做直线运动
图2
解析 根据等势线与电场线的关系,分别作出过M点和P点的等势线,M与P不在一条等势线上,因沿电场线方向电势降低,所以M点的电势高于P点的电势,即选项A正确.O点电势高于P点电势,移动负电荷由O点移动到P点,电场力做负功,故选项B错误.从O到N电场线越来越稀,表明从O到N电场强度越来越小,而OM=MN,所以M、N两点间的电势差低于O、M两点间的电势差,故C选项错误.沿y轴的电场强度的方向沿y轴的正方向,从O点释放一静止的带正电粒子,所受电场力的方向沿y轴正方向,因此带电粒子将沿y轴正方向做直线运动,故D对.
答案 AD
预测1 研究表明,无限大的均匀带电平面在周围空间会形成与平面垂直的匀强电场.现有两块无限大的均匀绝缘带电平面,一块带正电,一块带负电,把它们放置(如图3)所示,单位面积所带电荷的数值相等.图3中直线A1B1和A2B2分别为带正电和带负电的平面与纸面正交的交线,O为两交线的交点,两平面间绝缘,则下面四个选项中能正确反映等势面分布情况的是 ( )
图3
解析 带正电的平面A1B1在平面上方产生的匀强电场方向向上,在平面下方产生的匀强电场方向向下;带负电的平面A2B2在平面左边产生的电场方向向右,在平面右边产生的电场方向向左;空间电场为两电场的矢量和,在各象限内的电场如图所示,由电场线与等势面处垂直可知,A图正确.
答案 A
解题归纳 电场的描述一般从两个方面展开:
(1)力的性质E= ;(2)能的性质φ=
类型二 带电粒子在电场中的加速和偏转
例2 如图4所示为研究电子枪中电子在电场中运动的简化模型示意图.在Oxy平面的ABCD区域内,存在两个场强大小均为E的匀强电场Ⅰ和Ⅱ,两电场的边界是边长为L的正方形(不计电子所受重力).
(1)在该区域AB边的中点处由静止释放电子,求电子离开ABCD区域的位置;
(2)在电场Ⅰ区域内适当位置由静止释放电子,电子恰能从ABCD区域左下角D处离开,求所有释放点的位置;
(3)若将左侧电场Ⅱ整体水平向右移动L/n(n≥1),仍使电子从ABCD区域左下角D处离开(D不随电场移动),求在电场Ⅰ区域内由静止释放电子的所有位置.
图4
解析 (1)设电子的质量为m,电量为e,电子在电场Ⅰ中做匀加速直线运动,出区域Ⅰ时的速度为v0,此后在电场Ⅱ内做类平抛运动,假设电子从CD边射出,出射点的纵坐标为y,有eEL= mv02; -y
= at2=
解得y= L,所以原假设成立,即电子离开ABCD区域的位置坐标为(-2L, L)
(2)设释放点在电场区域Ⅰ中,其坐标为(x,y),在电场Ⅰ中电子被加速到v1,然后进入电场Ⅱ做类平抛运动,并从D点离开,有
eEx= mv12
y= at2=
解得xy= ,即在电场Ⅰ区域内满足方程的点即为所求位置.
(3)设电子从(x,y)点释放,在电场Ⅰ中加速到v2,进入电场Ⅱ后做类平抛运动,在高度为y′处离开电场Ⅱ时的情景与(2)中类似,然后电子做匀速直线运动,经过D点,则有
eEx= mv22
y-y′= at2=
vy=at= ,y′=vy
解得xy=L2 ,即在电场Ⅰ区域内满足方程的点即为所求位置.
答案 (1)(-2L, )(2)xy=
(3)xy=
解题归纳 本题考查了考生对牛顿第二定律、动能定理、运动学基本规律、平抛运动及其分析处理方法的理解.着重考查了考生的理解能力、推理能力和分析综合能力,题目难度较大,搞清楚带电粒子在不同过程的衔接点即中间转折状态是解题的关键.
预测2 静电喷漆技术具有效率高,浪
费少,质量好,有利于工人健康等
优点,其装置如图5所示.A、B为两
块平行金属板,间距d=0.40 m,两板
间有方向由B指向A,大小为E=1.0×103 N/C的匀强电场.在A板中央放置一个安全接地的静电油漆喷枪P,油漆喷呛的半圆形喷嘴可向各个方向均匀地喷出带电油漆微粒,油漆微粒的初速度大小均为v0=2.0 m/s,质量m=5.0×10-15 kg,电荷量为q=-2.0×10-16C.微粒的重力和所受空气阻力均不计,油漆微粒最后都落在金属板B上.试求:
图5
(1)电场力对每个微粒所做的功;
(2)微粒打在B板上的速度;
(3)微粒最后落在B板上所形成的图形及其面积的大小.
解析 (1)由电场力做功可知W=qEd=8.0×10-14J.
(2)由动能定理可得W= mv2- mv02,得v=6.0 m/s.
(3)微粒最后落在B板上所形成的图形为圆形
微粒运动的加速度a= ,而d= at12,R=v0t1,所以圆的面积S=πR2,综合以上各式并代入数据可得
S=0.25 m2.
答案 (1)8.0×10-14J (2)6.0 m/s (3)圆形0.25 m2
解题归纳 忽略带电粒子的重力和空气阻力,速度方向沿竖直方向的粒子的运动为类平抛运动,研究的方法和平抛运动类似,但要注意克服思维定势,要具体分析物体的初速度方向和受力方向,不要总认为水平方向匀速,竖直方向匀变速.还要注意类平抛运动和平抛运动的区别:所有平抛运动的加速度都是重力加速度,而带电粒子的类平抛运动的加速度a= ,
要具体问题具体分析,并且加速度可能会随着两板间距离的变化、电势差的变化而变化.
类型三 带电粒子在交变电场中的运动
例3 如图6甲所示,水平放置的平行金属板A和B的距离为d,它们的右端安放着垂直于金属板的靶MN,现在A、B板上加上如图乙所示的方波电压,电压的正向值为U0,反向电压值U0/2,且每隔T/2换向一次.现有质量为m、带正电且电荷量为q的粒子组成的粒子束从A、B的中点O沿平行于金属板方向OO′射入,设粒子能全部打在靶上且所有粒子在A、B间的飞行时间均为T.不计重力的影响,试求在靶MN上距其中心O′点多远的范围内有粒子击中?
图6
解析 若粒子在正向电压开始射入平行金属板A、B间.在前T/2时间内,粒子向下偏转,粒子沿电场方向的加速度大小a1=
竖直位移x1= a1t2=
T/2末的竖直分速度v1=a1·
在后T/2时间内,粒子沿电场方向的加速度大小
a2=
竖直位移x2=v1
粒子打在O′点正下方的最大位移为x=x1+x2=
若粒子在反向电压开始时射入平行金属板A、B间.在前T/2时间内,粒子向上偏转,粒子沿电场方向的加速度大小a1′=
T/2末的竖直分速度v1′=a1′·
竖直位移x1′= a1′t2=
在后T/2时间内,粒子沿电场方向的加速度大小
a2′=
竖直位移x2′=v1′T/2- a2′t2= · · -
· =0
粒子打在O′点正上方的最大位移为x′=x1′+x2′=
所以,在靶MN上O′点正上方 处与O′点正下方 处之间的范围内有粒子击中.
答案 见解析
类型四 电场综合应用
例4 如图7甲所示,在场强大小为E、方向竖直向下的匀强电场内存在一个半径为R的圆形区域,O点为该圆形区域的圆心,A点是圆形区域的最高点,B点是圆形区域最右侧的点.在A点由放射源释放出初速度大小不同、方向均垂直于场强向右的正电荷,电荷的质量为m,电荷量为q,不计电荷的重力.
图7
(1)正电荷以多大的速率发射,才能经过图中的P点(图甲中∠POA′=θ为已知)?
(2)在问题(1)中,正电荷经过P点的动能是多大?
(3)若在圆形区域的边缘有一接收屏CBD,其中C、D分别为接收屏上最边缘的两点(如图乙所示),且∠COB=∠BOD=30?;则该屏上接收到的正电荷的最大动能是多少?
解析 (1)正电荷做类平抛运动,则
a= ①
Rsin θ=v0t ②
R+Rcos θ= at2 ③
由以上三式解得v0= ④
(2)由④式可得正电荷从A点出发时的动能为
Ek0= mv02= ,则经过P点时的动能为Ek=qE(R+Rcos θ)+ mv02= qER(5+3cos θ) ⑤
(3)从⑤式可以看出,当θ从0?到180?变化过程中,接收屏上正电荷的动能逐渐减小,即θ越小接收的正电荷动能越大,因此D点接收到的正电荷的末动能最大.最大动能为:
EkD= qER(5+3 cos 60?)= qER.
答案 (1)
(2) qER(5+3cos θ)
(3) qER
解题归纳 正电荷在电场中受到电场力作用,电场力与初速度方向垂直且恒定,因此正电荷做类平抛运动,用正交分解法分析即可确定经过P点正电荷的初速度,再由动能定理即可求出正电荷经过P点时的动能;正电荷的动能是一个关于角θ的函数,利用数学方法可求出CBD屏上接收到的正电荷的动能的最大值.
1.(2009·徐州模拟)如图所示的真空空间中,仅在正方体中的黑点处存在着电荷量大小相等的点电荷,则图中a、b两点电场强度和电势均相同的是 ( )
解析 根据场强叠加的矢量性,及等量异种电荷、等量同种电荷中线上场强分析规律可判断C选项正确.
C
2. (2009·大连模拟)如图8所示,三个同心圆是点电荷Q周围的三个等势面,已知这三个圆的半径成等差数列,A、B、C分别是这三个等势面上的点,且这三点在同一条电场线上.将电量为q=+1.6×10-6C的电荷从A点移到C点,电势能减少1.92×10-5J,若取C点为电势零点(φ=0),则B点的电势是( )
A.一定等于6 V B.一定低于6 V
C.一定高于6 V D.无法确定
图8
解析 UAC= =12 V
由于从A→C场强逐渐减小,所以UAB>UBC.若选φC=0,则φB<6 V.
答案 B
3.(2009·上海质检)研究发现,某类微观带电粒子
之间的相互作用力F与它们之间的距离r的关系为:
式中F0为大于零的常量,负号表示引力.用U表示这类微观带电粒子间的势能,令U0=F0(r2-r1),取无穷远为势能零点,下列U-r图象正确的是 ( )
解析 当r>r2时,F=0,电场力不做功,电势能不变,即为0;当r1≤r≤r2时,电场力为-F0,所以从r2→r1电势能减小;当r
4.(2009·海南卷·10)如图9所示,
两等量异号的点电荷相距为a.M
与两点电荷共线,N位于两点电
荷连线的中垂线上,两点电荷连
线中点到M和N的距离都为L,且
L?a.略去(a/L)n(n≥2) 项的
贡献,则两点电荷的合电场在M和N点的强度
( )
A.大小之比为2,方向相反
B.大小之比为1,方向相反
C.大小均与a成正比,方向相反
D.大小均与L的平方成反比,方向相互垂直
图9
解析 如下图所示,合电场在M和N点的强度分别为
E1= ,E2= ,E1∶E2=2;又N点处强场方向由+q指向-q,在M点的场强表现+q的点电荷、由-q指向+q.
答案 AC
5. (2009·上海虹口区)如图10所示,
一竖直固定且光滑绝缘的直圆筒底
部放置一可视为点电荷的 场源电荷
A,其电荷量Q=+4×10-3C,场源电
荷A形成的电场中各点的电势表达式
为φ= ,其中k为静电力恒量,r
为空间某点到A的距离.现有一个质量
为m=0.1 kg的带正电的小球B,它与A球间的距离为a=0.4 m,此时小球B处于平衡状态,且小球B在场源电荷A形成的电场中具有电势能表达式为?= ,其中r为q与Q之间的距离.另一质量也为m的
图10
不带电绝缘小球C从距离B的上方H=0.8 m处自由下
落,落在小球B上立刻与小球B粘在一起以2 m/s向
下运动,它们到达最低点后又向上运动,向上运动
到达的最高点为P0(取g=10 m/s2,k=9×109 N·m2/C2),
求:
(1)小球C与小球B碰撞前的速度大小v0为多少?
(2)小球B的带电量q为多少?
(3)P点与小球A之间的距离为多大?
(4)当小球B和C一起向下运动与场源电荷A距离多远时,其速度最大?速度的最大值为多少?
解析 (1)小球C自由下落H距离的速度
v0= =4 m/s
(2)小球B在碰撞前处于平衡状态,对B球进行受力分析知:mg=k
代入数据得q = ×10-8C
(3)C和B向下运动到最低点后又向上运动到P点,运动过程中系统能量守恒,设P与A之间的距离为x,由能量守恒得
代入数据得x=0.68 m或x=(0.4+ )m
(4)当C和B向下运动的速度最大时,与A之间的距离为y,对C和B整体受力分析有:2mg=k ,
代入数据有y=0.28 m(或y= m)
由能量守恒得
·2mv2+k = ·2mvm2-2mg(a-y)+k
代入数据得vm=2.16 m/s(或vm= m/s)
答案 (1)4 m/s (2) ×10-8C (3)0.68 m
(4)0.28 m 2.16 m/s
返回
