人教版数学九年级下册 27.2相似三角形1学案
文档属性
| 名称 | 人教版数学九年级下册 27.2相似三角形1学案 |
|
|
| 格式 | zip | ||
| 文件大小 | 62.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 00:00:00 | ||
图片预览

文档简介
27.2相似三角形
【学习目标】
1.通过一些具体的情境和应用,深化对三角形的理解和认识.
2.能利用相似三角形的性质,分析和解决有关实际问题.
【基础知识精讲】
1.相似三角形的定义
对应角相等,对应边成比例的三角形叫做相似三角形.
2.能根据相似三角形的定义,判断两个三角形是否相似.要判断是否相似,必须满足两个条件:①所有的对应边成比例;②所有的对应角相等.如两个等腰三角形未必相似.
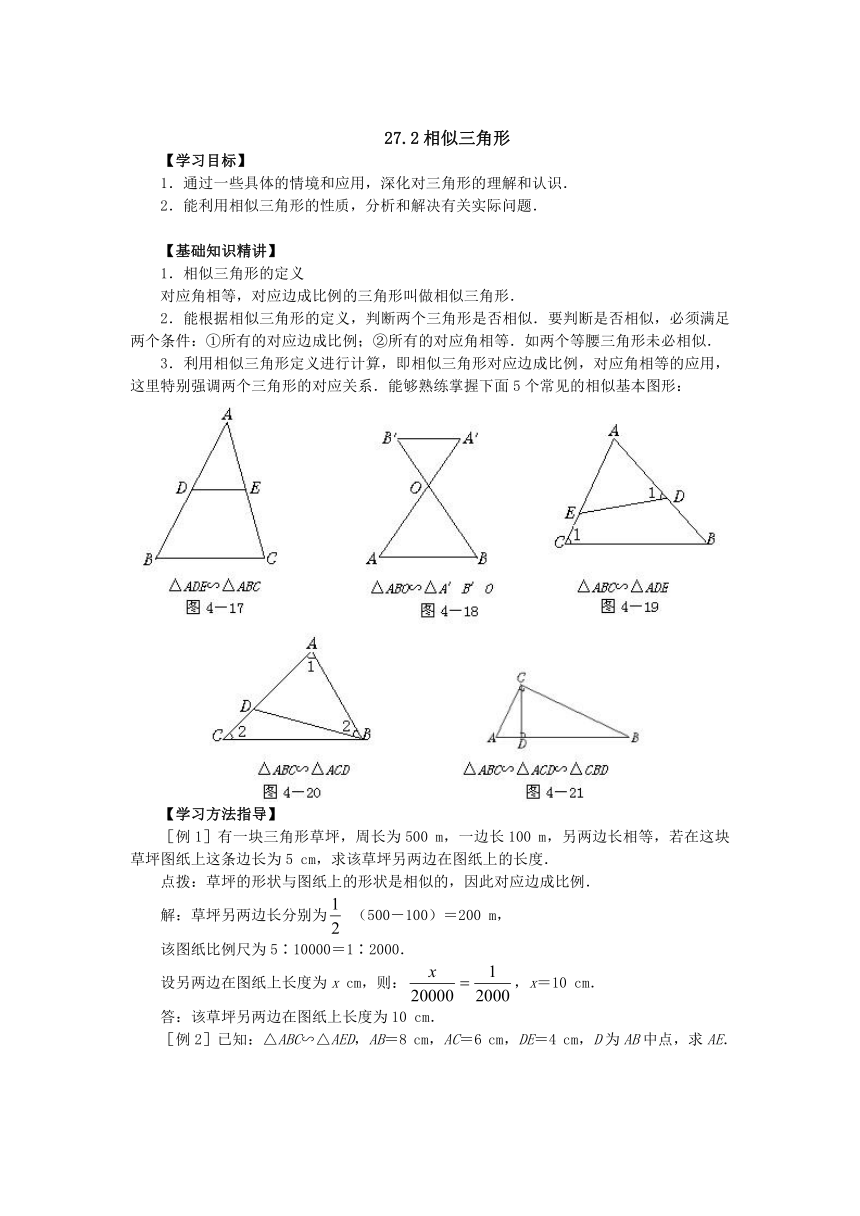
3.利用相似三角形定义进行计算,即相似三角形对应边成比例,对应角相等的应用,这里特别强调两个三角形的对应关系.能够熟练掌握下面5个常见的相似基本图形:
【学习方法指导】
[例1]有一块三角形草坪,周长为500
m,一边长100
m,另两边长相等,若在这块草坪图纸上这条边长为5
cm,求该草坪另两边在图纸上的长度.
点拨:草坪的形状与图纸上的形状是相似的,因此对应边成比例.
解:草坪另两边长分别为
(500-100)=200
m,
该图纸比例尺为5∶10000=1∶2000.
设另两边在图纸上长度为x
cm,则:,x=10
cm.
答:该草坪另两边在图纸上长度为10
cm.
[例2]已知:△ABC∽△AED,AB=8
cm,AC=6
cm,DE=4
cm,D为AB中点,求AE.
图4-22
点拨:利用中点定义,先求AD的大小,再由相似三角形性质,列比例等式计算.
解:∵AB=8
cm,D为AB中点,
∴AD=×8=4
cm.
又∵△ABC∽△AED,∴.
∵AC=6
cm,AB=8
cm,∴,
∴AE=
cm.
[例3]已知:Rt△ABC∽Rt△ADC,若AC=3,BC=4,求AD.
点拨:由Rt△ABC∽Rt△ACD可得:
,但此式中,AB、AD却不知道,要求AD,必须先求AB,已知的AC、BC,通过勾股定理求出AB,即可解决.
解:∵在Rt△ABC中,AC=3,BC=4,.
∴AB=5.
又∵Rt△ABC∽Rt△ACD,
∴,,∴AD=.
【拓展训练】
迁移
你能用本节课的知识解决下面问题吗?
1.若△ABC∽△A′B′C′,且△ABC三边之比为2∶3∶4,而△A′B′C′的最大边为12
cm,那么△A′B′C′的周长多大?
点拨:已知条件中的“△ABC三边之比为2∶3∶4”,由于△ABC∽△A′B′C′,因此△A′B′C′三边之比为2∶3∶4.
解:∵△ABC∽△A′B′C′,且△ABC三边之比为2∶3∶4.
∴△A′B′C′三边之比为2∶3∶4,
设△A′B′C′的边长分别为x、y,则,
∴x=6,y=9,∴△A′B′C′周长为6+9+12=27(cm).
2.两个相似三角形的一对对应边长分别为35
cm和14
cm,它们的周长相差60
cm,求这两个三角形的周长?
点拨:相似三角形的周长比等于相似比.
解:设较小三角形周长为x
cm,
∵两个三角形相似,∴
35x=14(x+60)
35x=14x+840
21x=840
x=40
较大三角形周长为40+60=100
cm.
答:两个三角形周长分别为40
cm和100
cm.
3.小明要做两个形状相同的三角形框架,其中一个框架三边为30
cm、40
cm、50
cm,而另一个三角形框架现在只有一条60
cm的木条,小明应该再找两根多长的木条呢?
点拨:此题的关键是弄清60
cm的木条和已知框架三边中的哪条边是对应边,因此有三种可能性,应分别讨论.
解:设另两条木条分别长x
cm,y
cm,
①若60
cm和30
cm木条为对应边时,
则,
x=80
cm,y=100
cm.
②若60
cm和40
cm木条为对应边时,
则,
x=45
cm,y=75
cm.
③若60
cm和50
cm木条为对应边时,
则=,
x=36
cm,y=48
cm.
发散
本节课会用到下列知识
1.相似三角形的对应边成比例.
2.相似三角形的周长之比等于相似比.
3.勾股定理.
【学习目标】
1.通过一些具体的情境和应用,深化对三角形的理解和认识.
2.能利用相似三角形的性质,分析和解决有关实际问题.
【基础知识精讲】
1.相似三角形的定义
对应角相等,对应边成比例的三角形叫做相似三角形.
2.能根据相似三角形的定义,判断两个三角形是否相似.要判断是否相似,必须满足两个条件:①所有的对应边成比例;②所有的对应角相等.如两个等腰三角形未必相似.
3.利用相似三角形定义进行计算,即相似三角形对应边成比例,对应角相等的应用,这里特别强调两个三角形的对应关系.能够熟练掌握下面5个常见的相似基本图形:
【学习方法指导】
[例1]有一块三角形草坪,周长为500
m,一边长100
m,另两边长相等,若在这块草坪图纸上这条边长为5
cm,求该草坪另两边在图纸上的长度.
点拨:草坪的形状与图纸上的形状是相似的,因此对应边成比例.
解:草坪另两边长分别为
(500-100)=200
m,
该图纸比例尺为5∶10000=1∶2000.
设另两边在图纸上长度为x
cm,则:,x=10
cm.
答:该草坪另两边在图纸上长度为10
cm.
[例2]已知:△ABC∽△AED,AB=8
cm,AC=6
cm,DE=4
cm,D为AB中点,求AE.
图4-22
点拨:利用中点定义,先求AD的大小,再由相似三角形性质,列比例等式计算.
解:∵AB=8
cm,D为AB中点,
∴AD=×8=4
cm.
又∵△ABC∽△AED,∴.
∵AC=6
cm,AB=8
cm,∴,
∴AE=
cm.
[例3]已知:Rt△ABC∽Rt△ADC,若AC=3,BC=4,求AD.
点拨:由Rt△ABC∽Rt△ACD可得:
,但此式中,AB、AD却不知道,要求AD,必须先求AB,已知的AC、BC,通过勾股定理求出AB,即可解决.
解:∵在Rt△ABC中,AC=3,BC=4,.
∴AB=5.
又∵Rt△ABC∽Rt△ACD,
∴,,∴AD=.
【拓展训练】
迁移
你能用本节课的知识解决下面问题吗?
1.若△ABC∽△A′B′C′,且△ABC三边之比为2∶3∶4,而△A′B′C′的最大边为12
cm,那么△A′B′C′的周长多大?
点拨:已知条件中的“△ABC三边之比为2∶3∶4”,由于△ABC∽△A′B′C′,因此△A′B′C′三边之比为2∶3∶4.
解:∵△ABC∽△A′B′C′,且△ABC三边之比为2∶3∶4.
∴△A′B′C′三边之比为2∶3∶4,
设△A′B′C′的边长分别为x、y,则,
∴x=6,y=9,∴△A′B′C′周长为6+9+12=27(cm).
2.两个相似三角形的一对对应边长分别为35
cm和14
cm,它们的周长相差60
cm,求这两个三角形的周长?
点拨:相似三角形的周长比等于相似比.
解:设较小三角形周长为x
cm,
∵两个三角形相似,∴
35x=14(x+60)
35x=14x+840
21x=840
x=40
较大三角形周长为40+60=100
cm.
答:两个三角形周长分别为40
cm和100
cm.
3.小明要做两个形状相同的三角形框架,其中一个框架三边为30
cm、40
cm、50
cm,而另一个三角形框架现在只有一条60
cm的木条,小明应该再找两根多长的木条呢?
点拨:此题的关键是弄清60
cm的木条和已知框架三边中的哪条边是对应边,因此有三种可能性,应分别讨论.
解:设另两条木条分别长x
cm,y
cm,
①若60
cm和30
cm木条为对应边时,
则,
x=80
cm,y=100
cm.
②若60
cm和40
cm木条为对应边时,
则,
x=45
cm,y=75
cm.
③若60
cm和50
cm木条为对应边时,
则=,
x=36
cm,y=48
cm.
发散
本节课会用到下列知识
1.相似三角形的对应边成比例.
2.相似三角形的周长之比等于相似比.
3.勾股定理.
