2020年秋人教版数学九年级上《弧长与扇形的面积》夯基练习卷 (word版含答案)
文档属性
| 名称 | 2020年秋人教版数学九年级上《弧长与扇形的面积》夯基练习卷 (word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 246.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 10:39:59 | ||
图片预览


文档简介
2020年人教版数学九上《弧长与扇形的面积》夯基练习卷
一、选择题
有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为(
)
A.
B.π
C.2π
D.3π
如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则弧CD的长为(
)
A.2π
B.4π
C.
D.
如图,在半径为5的⊙O中,将劣弧AB沿弦AB翻折,使折叠后的弧AB恰好与OA、OB相切,则劣弧AB的长为(
)
A.
B.
C.
D.
一个扇形的圆心角是60°,半径是6cm,那么这个扇形的面积是(
)
A.3πcm2
B.πcm2
C.6πcm2
D.9πcm2
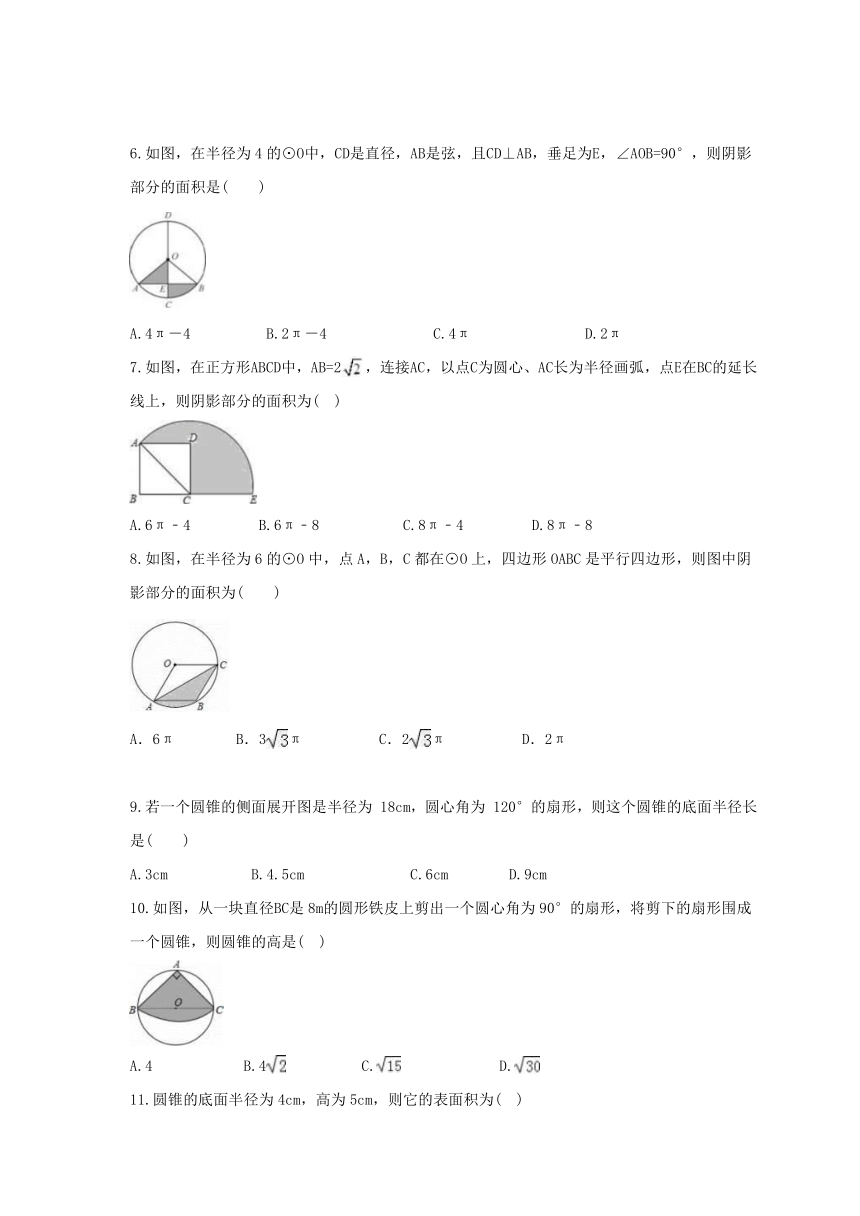
如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是(
)
A.4π-4
B.2π-4
C.4π
D.2π
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为(
)
A.6π﹣4
B.6π﹣8
C.8π﹣4
D.8π﹣8
如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π??
?
B.3π???
?
C.2π???
?
D.2π
若一个圆锥的侧面展开图是半径为
18cm,圆心角为
120°的扇形,则这个圆锥的底面半径长是(
)
A.3cm
B.4.5cm
C.6cm
D.9cm
如图,从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,则圆锥的高是(
)
A.4
B.4
C.
D.
圆锥的底面半径为4cm,高为5cm,则它的表面积为(
)
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
如图,正三角形ABC的边长为4cm,D,E,F分别为BC,AC,AB的中点,以A,B,C三点为圆心,2cm为半径作圆.则图中阴影部分面积为(
)
A.(2-π)cm2
B.(π-)cm2
C.(4-2π)cm2
D.(2π-2)cm2
二、填空题
如图,折扇的骨柄长为27cm,折扇张开的角度为120°,图中的长为 ?
cm(结果保留π).
如图,小正方形的边长均为1,点B、O都在格点上,以O为圆心,OB为半径画弧,如图所示,则劣弧BC的长是 .
已知圆锥的底面圆的半径是2.5,母线长是9,其侧面展开图的圆心角是________度.
如图,圆锥的母线长为10,侧面展开图的面积为60π,则圆锥主视图面积为__________.
如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,则阴影部分的面积为___________(结果保留π.
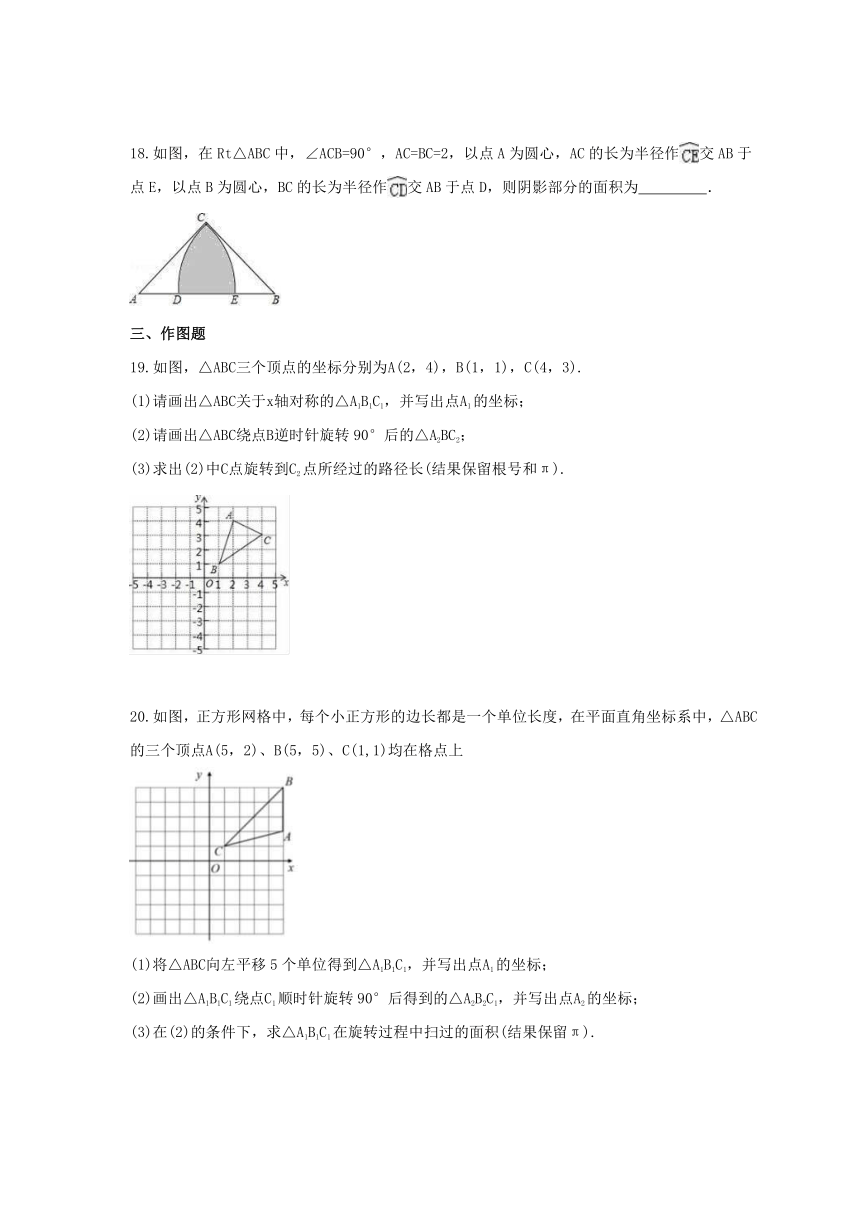
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作交AB于点E,以点B为圆心,BC的长为半径作交AB于点D,则阴影部分的面积为 ??
.
三、作图题
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上
(1)将△ABC向左平移5个单位得到△A1B1C1,并写出点A1的坐标;
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1,并写出点A2的坐标;
(3)在(2)的条件下,求△A1B1C1在旋转过程中扫过的面积(结果保留π).
四、解答题
如图,AB是⊙O的直径,点C是圆上一点,连接CA、CB,过点O作弦BC的垂线,交于点D,连接AD.
(1)求证:∠CAD=∠BAD;
(2)若⊙O的半径为1,∠B=50°,求的长.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠CAE=∠B=60°.
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
如图,已知AB是⊙O的直径,点C.答案为:D;在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.
如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,
=1.4,
=1.7).
参考答案
答案为:C;
答案为:A;
答案为:D;
答案为:B;
答案为:C;
答案为:D;
答案为:A;
答案为:A.
答案为:C;
答案为:D;.
答案为:D;
答案为:C;
答案为:18π.
答案为:π.
答案为:100.
答案为:48
答案为:π-2.
答案为:π﹣2.
解:
解:
(1)如图所示,;
(2)如图所示,
(3)
(1)证明:∵点O是圆心,OD⊥BC,
∴,
∴∠CAD=∠BAD;
(2)连接CO,
∵∠B=50°,
∴∠AOC=100°,
∴的长为:L=.
解:
(1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)略.
解:由题意可知:
=6π,
=4π,设∠AOB=n,AO=R,则CO=R﹣8,
由弧长公式得:
=4π,
∴,解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R﹣8=16,
∴S扇形OCD=0.5×4π×16=32π(cm2),S扇形OAB=0.5×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=72π﹣32π=40π(cm2),
纸杯底面积=π?22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
解:(1)连接OC,
∵∠D和∠AOC分别是弧AC所对的圆周角和圆心角,∠D=60°,
∴∠AOC=2∠D=120°,
∵OE⊥AC,
∴∠AOE=∠COE=0.5∠AOC=60°,∠OAE=30°.
∵AB是⊙O的直径,AB=6,
∴OA=3,
∴OE=0.5OA=1.5;
(2)∵OE=0.5OA,∴EF=OE.
∵OE⊥AC,
∴∠AEF=∠CEO=90°,AE=CE.
∴△AEF≌△CEO.
∴S阴影=S扇形COF=1.5π.
证明:(1)∵CD∥AB,∴∠CDA=∠BAD,
又∵OA=OD,∴∠ADO=∠BAD,∴∠ADO=∠CDA,∴DA平分∠CDO.
(2)如图,连接BD,∵AB是直径,∴∠ADB=90°,
∵AC=CD,∴∠CAD=∠CDA,又∵CD∥AB,∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,∴==,
又∵∠AOB=180°,∴∠DOB=60°,
∵OD=OB,∴△DOB是等边三角形,∴BD=OB=AB=6,
∵=,∴AC=BD=6,∵BE切⊙O于B,∴BE⊥AB,∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,∴BE⊥CE,∴DE=BD=3,BE=BD×cos∠DBE=6×=3,
∴的长==2π,
∴图中阴影部分周长之和为2=4π+9+3=4×3.1+9+3×1.7=26.5.
一、选择题
有一条弧的长为2πcm,半径为2cm,则这条弧所对的圆心角的度数是(
)
A.90°
B.120°
C.180°
D.135°
如图,在4×4的正方形网格中,每个小正方形的边长都为1,△AOB的三个顶点都在格点上,现将△AOB绕点O逆时针旋转90°后得到对应的△COD,则点A经过的路径弧AC的长为(
)
A.
B.π
C.2π
D.3π
如图,AB是⊙O的直径,CD是弦,点C,D在直径AB的两侧.若∠AOC:∠AOD:∠DOB=2:7:11,CD=4,则弧CD的长为(
)
A.2π
B.4π
C.
D.
如图,在半径为5的⊙O中,将劣弧AB沿弦AB翻折,使折叠后的弧AB恰好与OA、OB相切,则劣弧AB的长为(
)
A.
B.
C.
D.
一个扇形的圆心角是60°,半径是6cm,那么这个扇形的面积是(
)
A.3πcm2
B.πcm2
C.6πcm2
D.9πcm2
如图,在半径为4的⊙O中,CD是直径,AB是弦,且CD⊥AB,垂足为E,∠AOB=90°,则阴影部分的面积是(
)
A.4π-4
B.2π-4
C.4π
D.2π
如图,在正方形ABCD中,AB=2,连接AC,以点C为圆心、AC长为半径画弧,点E在BC的延长线上,则阴影部分的面积为(
)
A.6π﹣4
B.6π﹣8
C.8π﹣4
D.8π﹣8
如图,在半径为6的⊙O中,点A,B,C都在⊙O上,四边形OABC是平行四边形,则图中阴影部分的面积为( )
A.6π??
?
B.3π???
?
C.2π???
?
D.2π
若一个圆锥的侧面展开图是半径为
18cm,圆心角为
120°的扇形,则这个圆锥的底面半径长是(
)
A.3cm
B.4.5cm
C.6cm
D.9cm
如图,从一块直径BC是8m的圆形铁皮上剪出一个圆心角为90°的扇形,将剪下的扇形围成一个圆锥,则圆锥的高是(
)
A.4
B.4
C.
D.
圆锥的底面半径为4cm,高为5cm,则它的表面积为(
)
A.12πcm2
B.26πcm2
C.πcm2
D.(4+16)πcm2
如图,正三角形ABC的边长为4cm,D,E,F分别为BC,AC,AB的中点,以A,B,C三点为圆心,2cm为半径作圆.则图中阴影部分面积为(
)
A.(2-π)cm2
B.(π-)cm2
C.(4-2π)cm2
D.(2π-2)cm2
二、填空题
如图,折扇的骨柄长为27cm,折扇张开的角度为120°,图中的长为 ?
cm(结果保留π).
如图,小正方形的边长均为1,点B、O都在格点上,以O为圆心,OB为半径画弧,如图所示,则劣弧BC的长是 .
已知圆锥的底面圆的半径是2.5,母线长是9,其侧面展开图的圆心角是________度.
如图,圆锥的母线长为10,侧面展开图的面积为60π,则圆锥主视图面积为__________.
如图,在△ABC中,∠ABC=90°,AB=BC=2,以点C为圆心,线段CA的长为半径作弧AD,交CB的延长线于点D,则阴影部分的面积为___________(结果保留π.
如图,在Rt△ABC中,∠ACB=90°,AC=BC=2,以点A为圆心,AC的长为半径作交AB于点E,以点B为圆心,BC的长为半径作交AB于点D,则阴影部分的面积为 ??
.
三、作图题
如图,△ABC三个顶点的坐标分别为A(2,4),B(1,1),C(4,3).
(1)请画出△ABC关于x轴对称的△A1B1C1,并写出点A1的坐标;
(2)请画出△ABC绕点B逆时针旋转90°后的△A2BC2;
(3)求出(2)中C点旋转到C2点所经过的路径长(结果保留根号和π).
如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,△ABC的三个顶点A(5,2)、B(5,5)、C(1,1)均在格点上
(1)将△ABC向左平移5个单位得到△A1B1C1,并写出点A1的坐标;
(2)画出△A1B1C1绕点C1顺时针旋转90°后得到的△A2B2C1,并写出点A2的坐标;
(3)在(2)的条件下,求△A1B1C1在旋转过程中扫过的面积(结果保留π).
四、解答题
如图,AB是⊙O的直径,点C是圆上一点,连接CA、CB,过点O作弦BC的垂线,交于点D,连接AD.
(1)求证:∠CAD=∠BAD;
(2)若⊙O的半径为1,∠B=50°,求的长.
如图,已知AB是⊙O的直径,点C,D在⊙O上,点E在⊙O外,∠CAE=∠B=60°.
(1)求∠ADC的度数;
(2)求证:AE是⊙O的切线;
(3)当BC=4时,求劣弧AC的长.
下图是一纸杯,它的母线AC和EF延长后形成的立体图形是圆锥.该圆锥的侧面展开图形是扇形OAB.经测量,纸杯上开口圆的直径为6cm,下底面直径为4cm,母线长EF=8cm.求扇形OAB的圆心角及这个纸杯的表面积.(面积计算结果用π表示).
如图,已知AB是⊙O的直径,点C.答案为:D;在⊙O上,∠D=60°且AB=6,过O点作OE⊥AC,垂足为E.
(1)求OE的长;
(2)若OE的延长线交⊙O于点F,求弦AF、AC和弧CF围成的图形(阴影部分)的面积.
如图,CD是⊙O的弦,AB是直径,且CD∥AB,连接AC、AD、OD,其中AC=CD,过点B的切线交CD的延长线于E.
(1)求证:DA平分∠CDO;
(2)若AB=12,求图中阴影部分的周长之和(参考数据:π=3.1,
=1.4,
=1.7).
参考答案
答案为:C;
答案为:A;
答案为:D;
答案为:B;
答案为:C;
答案为:D;
答案为:A;
答案为:A.
答案为:C;
答案为:D;.
答案为:D;
答案为:C;
答案为:18π.
答案为:π.
答案为:100.
答案为:48
答案为:π-2.
答案为:π﹣2.
解:
解:
(1)如图所示,;
(2)如图所示,
(3)
(1)证明:∵点O是圆心,OD⊥BC,
∴,
∴∠CAD=∠BAD;
(2)连接CO,
∵∠B=50°,
∴∠AOC=100°,
∴的长为:L=.
解:
(1)∵∠ABC与∠ADC都是弧AC所对的圆周角,
∴∠ADC=∠B=60°.
(2)∵AB是⊙O的直径,
∴∠ACB=90°,
∴∠BAC=30°.
∴∠BAE=∠BAC+∠EAC=30°+60°=90°,即?BA⊥AE.
∴AE是⊙O的切线.
(3)略.
解:由题意可知:
=6π,
=4π,设∠AOB=n,AO=R,则CO=R﹣8,
由弧长公式得:
=4π,
∴,解得:n=45,R=24,
故扇形OAB的圆心角是45度.
∵R=24,R﹣8=16,
∴S扇形OCD=0.5×4π×16=32π(cm2),S扇形OAB=0.5×6π×24=72π(cm2),
纸杯侧面积=S扇形OAB﹣S扇形OCD=72π﹣32π=40π(cm2),
纸杯底面积=π?22=4π(cm2)
纸杯表面积=40π+4π=44π(cm2).
解:(1)连接OC,
∵∠D和∠AOC分别是弧AC所对的圆周角和圆心角,∠D=60°,
∴∠AOC=2∠D=120°,
∵OE⊥AC,
∴∠AOE=∠COE=0.5∠AOC=60°,∠OAE=30°.
∵AB是⊙O的直径,AB=6,
∴OA=3,
∴OE=0.5OA=1.5;
(2)∵OE=0.5OA,∴EF=OE.
∵OE⊥AC,
∴∠AEF=∠CEO=90°,AE=CE.
∴△AEF≌△CEO.
∴S阴影=S扇形COF=1.5π.
证明:(1)∵CD∥AB,∴∠CDA=∠BAD,
又∵OA=OD,∴∠ADO=∠BAD,∴∠ADO=∠CDA,∴DA平分∠CDO.
(2)如图,连接BD,∵AB是直径,∴∠ADB=90°,
∵AC=CD,∴∠CAD=∠CDA,又∵CD∥AB,∴∠CDA=∠BAD,
∴∠CDA=∠BAD=∠CAD,∴==,
又∵∠AOB=180°,∴∠DOB=60°,
∵OD=OB,∴△DOB是等边三角形,∴BD=OB=AB=6,
∵=,∴AC=BD=6,∵BE切⊙O于B,∴BE⊥AB,∴∠DBE=∠ABE﹣∠ABD=30°,
∵CD∥AB,∴BE⊥CE,∴DE=BD=3,BE=BD×cos∠DBE=6×=3,
∴的长==2π,
∴图中阴影部分周长之和为2=4π+9+3=4×3.1+9+3×1.7=26.5.
同课章节目录
