1.6利用三角函数测高-北师大版九年级数学下册同步测试(Word版 含答案)
文档属性
| 名称 | 1.6利用三角函数测高-北师大版九年级数学下册同步测试(Word版 含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 226.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-16 22:25:38 | ||
图片预览



文档简介
北师大版九年级数学下册第一章1.6利用三角函数测高 同步测试
一.选择题
1.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
2.在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
3.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btanα B.a+bsinα C.a+ D.a+
4.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4km B.(2+false)km C.2falsekm D.(4-false)km
5.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
6.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100false B.200 C.100 D.200false
7.如图,为测量一根与地面垂直的旗杆AH的高度,在距离旗杆底端H10米的B处测得旗杆顶端A的仰角∠ABH=α,则旗杆AH的高度为( )
A.10sinα米 B.10cosα米 C.米 D.10tanα米
8.如图,一艘轮船在A处测得灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶40海里到达B处,测得灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.海里 B.海里 C.80海里 D.海里
9.温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10false千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
A.5 B.6 C.8 D.10
10.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里 C.6sin55°海里 D.6tan55°海里
11.如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan70°米 B.米 C.200sin 70°米 D.米
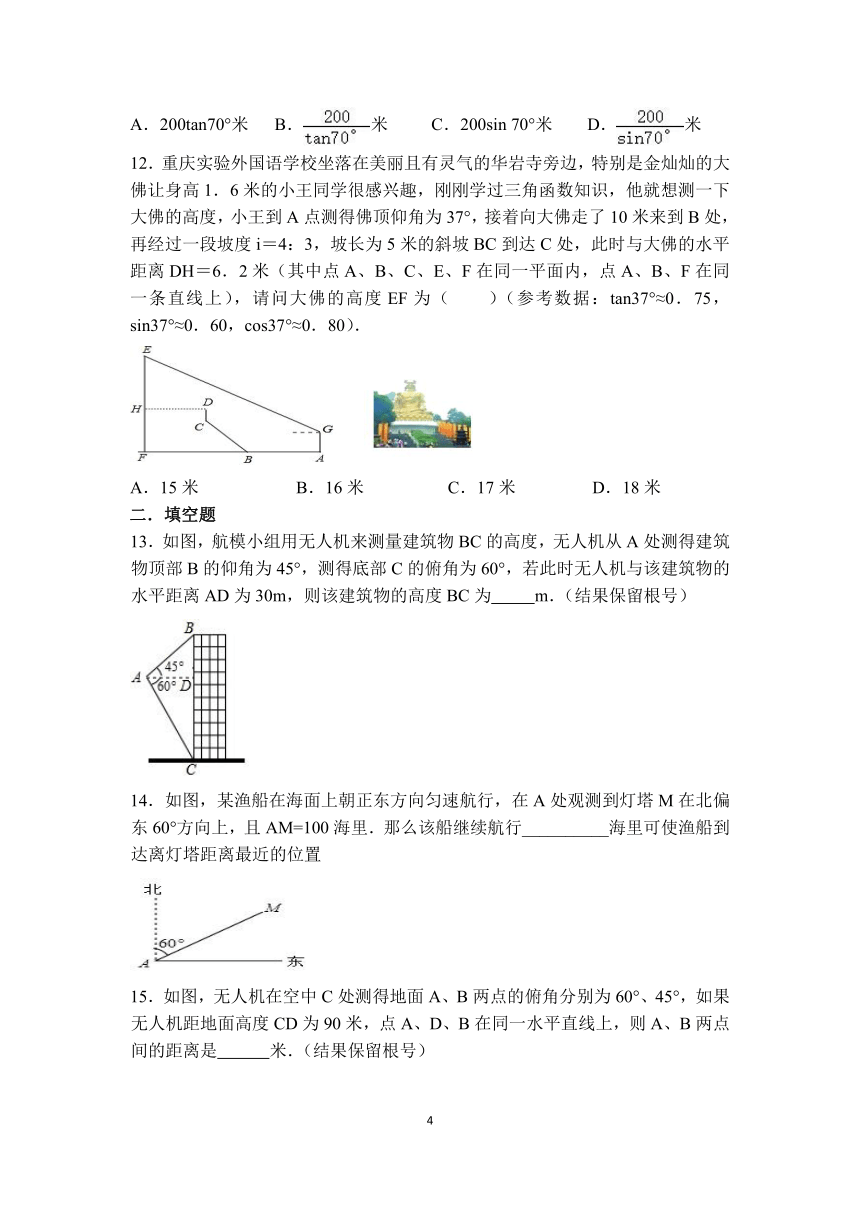
12.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
A.15米 B.16米 C.17米 D.18米
二.填空题
13.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为 m.(结果保留根号)
14.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行__________海里可使渔船到达离灯塔距离最近的位置
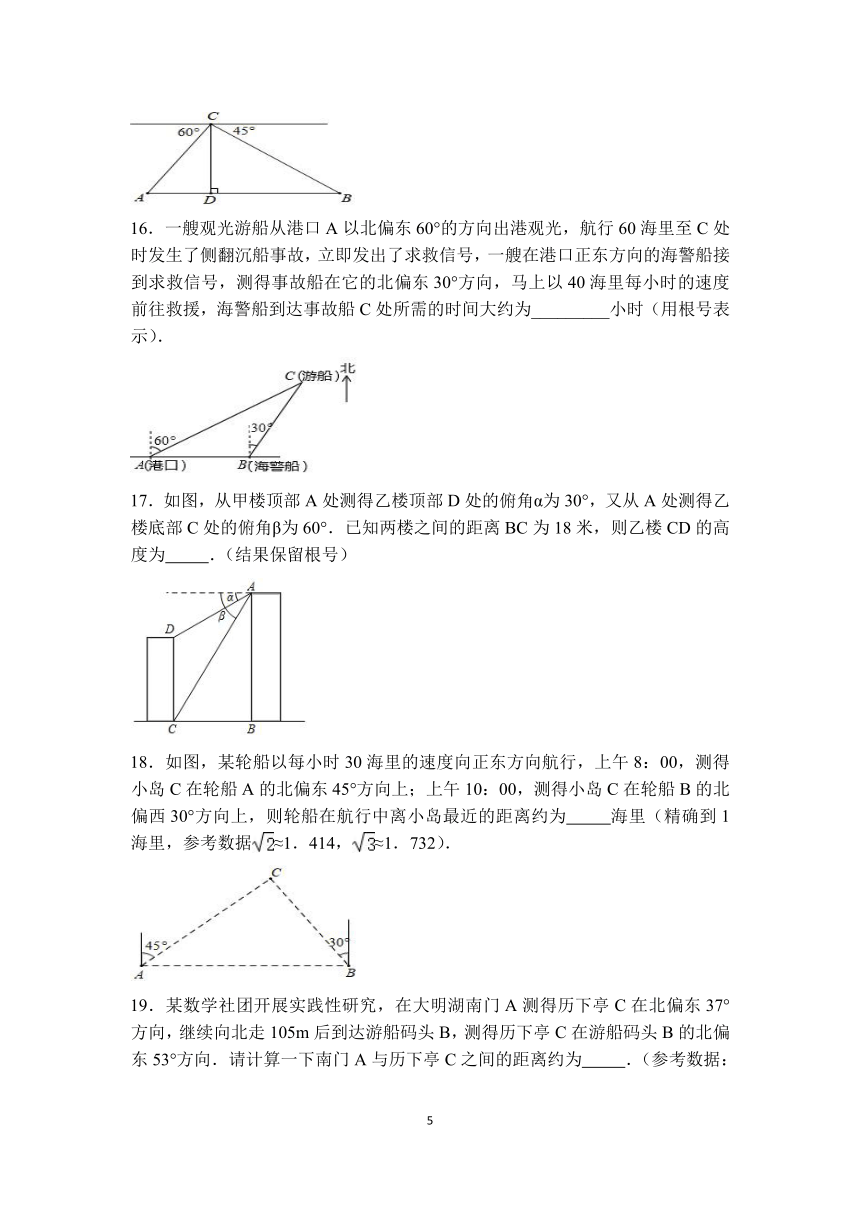
15.如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为90米,点A、D、B在同一水平直线上,则A、B两点间的距离是 米.(结果保留根号)
16.一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为_________小时(用根号表示).
17.如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°.已知两楼之间的距离BC为18米,则乙楼CD的高度为 .(结果保留根号)
18.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为 海里(精确到1海里,参考数据≈1.414,≈1.732).
19.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为 .(参考数据:tan37°≈,tan53°≈)
20.如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过几分钟后到达哨所东北方向的B处,此时该船距哨所的距离(OB)为 米.
三.解答题
21.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:false≈1.732)
22.某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号)
23.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
24.如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=5:12,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
25.游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
26.如图,小岛C和D都在码头O的正北方向上,它们之间距离为6.4km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28km/h,经过0.2h,渔船行驶到了B处,测得∠DBO=49°,求渔船在B处时距离码头O有多远?(结果精确到0.1km)
(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15)
答案提示
1.C.2.B.3.A.4.B.5.C.6.B.7.D.8.B.9.D.10.B.11.B.12.B.
13.(30+30). 14.false 15.(30+90) 16.false
17.12米. 18.38. 19.300m. 20.250.
21.解:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°-∠CAF=30°,
∴∠C=180°-∠CBA-∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°-∠CBE=60°,
∴CD=BC?sin∠CBD=20×false≈17(海里).
22.解:由题意得∠CAO=60°,∠CBO=45°,
∵OA=1800×tan30°=1800×=600,OB=OC=1800,
∴AB=(1800﹣600)(m).
答:隧道AB的长为(1800﹣600)m.
23.解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°-45°=45°,∠PAM=90°-60°=30°,AP=20海里,
∴PM=false AP=10海里,AM=cos30°AP=10false海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10false)海里,
∴BP=PM false=10false海里,
即小船到B码头的距离是10false海里,A、B两个码头间的距离是(10+10false)海里.
24.解:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5:12,
∴=,
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得,x=1,
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米;
(2)∵tan64°=,tan45°=,DE=5米,CE=12米,
∴2=,1=,
解得,AB=34米,AC=17米,
即大楼AB的高度是34米.
25.解:方法一:
过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
方法二:
由题意得:OB=12千米,∠AOB=30°,∠ABO=60°,
则∠OAB=90°,
故AB=OB=6(千米),
答:此时游艇与灯塔的距离AB为6千米.
26.解:设B处距离码头O有xkm,
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴CO=AO?tan∠CAO=(28×0.2+x)?tan26.5°≈2.8+0.5x(km),
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO?tan∠DBO=x?tan49°≈1.15x(km),
∵DC=DO﹣CO,
∴6.4=1.15x﹣(2.8+0.5x),
∴x≈14.2(km).
因此,B处距离码头O大约14.2km.
一.选择题
1.如图,在地面上的点A处测得树顶B的仰角为α度,AC=7m,则树高BC为(用含α的代数式表示)( )
A.7sinα B.7cosα C.7tanα D.
2.在一次夏令营活动中,小霞同学从营地A点出发,要到距离A点10千米的C地去,先沿北偏东70°方向走了8千米到达B地,然后再从B地走了6千米到达目的地C,此时小霞在B地的( )
A.北偏东20°方向上 B.北偏西20°方向上
C.北偏西30°方向上 D.北偏西40°方向上
3.如图,小明想要测量学校操场上旗杆AB的高度,他作了如下操作:(1)在点C处放置测角仪,测得旗杆顶的仰角∠ACE=α;
(2)量得测角仪的高度CD=a;
(3)量得测角仪到旗杆的水平距离DB=b.
利用锐角三角函数解直角三角形的知识,旗杆的高度可表示为( )
A.a+btanα B.a+bsinα C.a+ D.a+
4.如图,在一笔直的海岸线l上有A、B两个观测站,AB=2km、从A测得船C在北偏东45°的方向,从B测得船C在北偏东22.5°的方向,则船C离海岸线l的距离(即CD的长)为( )
A.4km B.(2+false)km C.2falsekm D.(4-false)km
5.如图,某校教学楼AB后方有一斜坡,斜坡与教学楼剖面在同一平面内,已知斜坡CD的长为6m,坡度i=1:0.75,教学楼底部到斜坡底部的水平距离AC=8m,在教学楼顶部B点测得斜坡顶部D点的俯角为46°,则教学楼的高度约为( )
(参考数据:sin46°≈0.72,cos46°≈0.69,tan46°≈1.04)
A.12.1m B.13.3m C.16.9m D.18.1m
6.如图,杭州市郊外一景区内有一条笔直的公路a经过两个景点A,B,景区管委会又开发了风景优美的景点C,经测量景点C位于景点A的北偏东60°方向,又位于景点B的北偏东30°方向,且景点A、B相距200m,则景点B、C相距的路程为( )
A.100false B.200 C.100 D.200false
7.如图,为测量一根与地面垂直的旗杆AH的高度,在距离旗杆底端H10米的B处测得旗杆顶端A的仰角∠ABH=α,则旗杆AH的高度为( )
A.10sinα米 B.10cosα米 C.米 D.10tanα米
8.如图,一艘轮船在A处测得灯塔C在北偏西15°的方向上,该轮船又从A处向正东方向行驶40海里到达B处,测得灯塔C在北偏西60°的方向上,则轮船在B处时与灯塔C之间的距离(即BC的长)为( )
A.海里 B.海里 C.80海里 D.海里
9.温州市处于东南沿海,夏季经常遭受台风袭击.一次,温州气象局测得台风中心在温州市A的正西方向300千米的B处(如图),以每小时10false千米的速度向东偏南30°的BC方向移动,并检测到台风中心在移动过程中,温州市A将受到影响,且距台风中心200千米的范围是受台风严重影响的区域.则影响温州市A的时间会持续多长?( )
A.5 B.6 C.8 D.10
10.如图,一艘海轮位于灯塔P的北偏东55°方向的A处,已知PA=6海里,如果海轮沿正南方向航行到灯塔的正东方向,则海轮航行的距离AB的长是( )
A.6海里 B.6cos55°海里 C.6sin55°海里 D.6tan55°海里
11.如图,为了测量一条河流的宽度,一测量员在河岸边相距200米的P、Q两点分别测定对岸一棵树T的位置,T在P的正北方向,且T在Q的北偏西70°方向,则河宽(PT的长)可以表示为( )
A.200tan70°米 B.米 C.200sin 70°米 D.米
12.重庆实验外国语学校坐落在美丽且有灵气的华岩寺旁边,特别是金灿灿的大佛让身高1.6米的小王同学很感兴趣,刚刚学过三角函数知识,他就想测一下大佛的高度,小王到A点测得佛顶仰角为37°,接着向大佛走了10米来到B处,再经过一段坡度i=4:3,坡长为5米的斜坡BC到达C处,此时与大佛的水平距离DH=6.2米(其中点A、B、C、E、F在同一平面内,点A、B、F在同一条直线上),请问大佛的高度EF为( )(参考数据:tan37°≈0.75,sin37°≈0.60,cos37°≈0.80).
A.15米 B.16米 C.17米 D.18米
二.填空题
13.如图,航模小组用无人机来测量建筑物BC的高度,无人机从A处测得建筑物顶部B的仰角为45°,测得底部C的俯角为60°,若此时无人机与该建筑物的水平距离AD为30m,则该建筑物的高度BC为 m.(结果保留根号)
14.如图,某渔船在海面上朝正东方向匀速航行,在A处观测到灯塔M在北偏东60°方向上,且AM=100海里.那么该船继续航行__________海里可使渔船到达离灯塔距离最近的位置
15.如图,无人机在空中C处测得地面A、B两点的俯角分别为60°、45°,如果无人机距地面高度CD为90米,点A、D、B在同一水平直线上,则A、B两点间的距离是 米.(结果保留根号)
16.一艘观光游船从港口A以北偏东60°的方向出港观光,航行60海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东30°方向,马上以40海里每小时的速度前往救援,海警船到达事故船C处所需的时间大约为_________小时(用根号表示).
17.如图,从甲楼顶部A处测得乙楼顶部D处的俯角α为30°,又从A处测得乙楼底部C处的俯角β为60°.已知两楼之间的距离BC为18米,则乙楼CD的高度为 .(结果保留根号)
18.如图,某轮船以每小时30海里的速度向正东方向航行,上午8:00,测得小岛C在轮船A的北偏东45°方向上;上午10:00,测得小岛C在轮船B的北偏西30°方向上,则轮船在航行中离小岛最近的距离约为 海里(精确到1海里,参考数据≈1.414,≈1.732).
19.某数学社团开展实践性研究,在大明湖南门A测得历下亭C在北偏东37°方向,继续向北走105m后到达游船码头B,测得历下亭C在游船码头B的北偏东53°方向.请计算一下南门A与历下亭C之间的距离约为 .(参考数据:tan37°≈,tan53°≈)
20.如图,某海防哨所(O)发现在它的北偏西30°,距离为500m的A处有一艘船,该船向正东方向航行,经过几分钟后到达哨所东北方向的B处,此时该船距哨所的距离(OB)为 米.
三.解答题
21.如图,某渔船在海面上朝正西方向以20海里/时匀速航行,在A处观测到灯塔C在北偏西60°方向上,航行1小时到达B处,此时观察到灯塔C在北偏西30°方向上,若该船继续向西航行至离灯塔距离最近的位置,求此时渔船到灯塔的距离(结果精确到1海里,参考数据:false≈1.732)
22.某高速公路建设中,需要确定隧道AB的长度.已知在离地面1800m高度C处的飞机上,测量人员测得正前方A,B两点处的俯角分别为60°和45°(即∠DCA=60°,∠DCB=45°).求隧道AB的长.(结果保留根号)
23.如图,在一笔直的海岸线l上有A、B两个码头,A在B的正东方向,一艘小船从A码头沿它的北偏西60°的方向行驶了20海里到达点P处,此时从B码头测得小船在它的北偏东45°的方向.求此时小船到B码头的距离(即BP的长)和A、B两个码头间的距离(结果都保留根号).
24.如图,在大楼AB的正前方有一斜坡CD,CD=13米,坡比DE:EC=5:12,高为DE,在斜坡下的点C处测得楼顶B的仰角为64°,在斜坡上的点D处测得楼顶B的仰角为45°,其中A、C、E在同一直线上.
(1)求斜坡CD的高度DE;
(2)求大楼AB的高度;(参考数据:sin64°≈0.9,tan64°≈2).
25.游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
26.如图,小岛C和D都在码头O的正北方向上,它们之间距离为6.4km,一艘渔船自西向东匀速航行,行驶到位于码头O的正西方向A处时,测得∠CAO=26.5°,渔船速度为28km/h,经过0.2h,渔船行驶到了B处,测得∠DBO=49°,求渔船在B处时距离码头O有多远?(结果精确到0.1km)
(参考数据:sin26.5°≈0.45,cos26.5°≈0.89,tan26.5°≈0.50,sin49°≈0.75,cos49°≈0.66,tan49°≈1.15)
答案提示
1.C.2.B.3.A.4.B.5.C.6.B.7.D.8.B.9.D.10.B.11.B.12.B.
13.(30+30). 14.false 15.(30+90) 16.false
17.12米. 18.38. 19.300m. 20.250.
21.解:如图,过点C作CD⊥AB于点D,
AB=20×1=20(海里),
∵∠CAF=60°,∠CBE=30°,
∴∠CBA=∠CBE+∠EBA=120°,∠CAB=90°-∠CAF=30°,
∴∠C=180°-∠CBA-∠CAB=30°,
∴∠C=∠CAB,
∴BC=BA=20(海里),
∠CBD=90°-∠CBE=60°,
∴CD=BC?sin∠CBD=20×false≈17(海里).
22.解:由题意得∠CAO=60°,∠CBO=45°,
∵OA=1800×tan30°=1800×=600,OB=OC=1800,
∴AB=(1800﹣600)(m).
答:隧道AB的长为(1800﹣600)m.
23.解:如图:
过P作PM⊥AB于M,
则∠PMB=∠PMA=90°,
∵∠PBM=90°-45°=45°,∠PAM=90°-60°=30°,AP=20海里,
∴PM=false AP=10海里,AM=cos30°AP=10false海里,
∴∠BPM=∠PBM=45°,
∴PM=BM=10海里,
∴AB=AM+BM=(10+10false)海里,
∴BP=PM false=10false海里,
即小船到B码头的距离是10false海里,A、B两个码头间的距离是(10+10false)海里.
24.解:(1)∵在大楼AB的正前方有一斜坡CD,CD=13米,坡度为5:12,
∴=,
设DE=5x米,则EC=12x米,
∴(5x)2+(12x)2=132,
解得,x=1,
∴5x=5,12x=12,
即DE=5米,EC=12米,
故斜坡CD的高度DE是5米;
(2)∵tan64°=,tan45°=,DE=5米,CE=12米,
∴2=,1=,
解得,AB=34米,AC=17米,
即大楼AB的高度是34米.
25.解:方法一:
过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=,tan60°=,
则OC=x,BC=x,
而OC+CB=x+x=12,
解得:x=3.
故AB===6(千米),
答:此时游艇与灯塔的距离AB为6千米.
方法二:
由题意得:OB=12千米,∠AOB=30°,∠ABO=60°,
则∠OAB=90°,
故AB=OB=6(千米),
答:此时游艇与灯塔的距离AB为6千米.
26.解:设B处距离码头O有xkm,
在Rt△CAO中,∠CAO=26.5°,
∵tan∠CAO=,
∴CO=AO?tan∠CAO=(28×0.2+x)?tan26.5°≈2.8+0.5x(km),
在Rt△DBO中,∠DBO=49°,
∵tan∠DBO=,
∴DO=BO?tan∠DBO=x?tan49°≈1.15x(km),
∵DC=DO﹣CO,
∴6.4=1.15x﹣(2.8+0.5x),
∴x≈14.2(km).
因此,B处距离码头O大约14.2km.
