北师大版七年级数学上册 第一章 丰富的图形世界 单元测试题(Word版 有答案)
文档属性
| 名称 | 北师大版七年级数学上册 第一章 丰富的图形世界 单元测试题(Word版 有答案) |  | |
| 格式 | docx | ||
| 文件大小 | 166.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 23:45:59 | ||
图片预览

文档简介
1049020010693400123190000第一章 丰富的图形世界 单元测试题
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
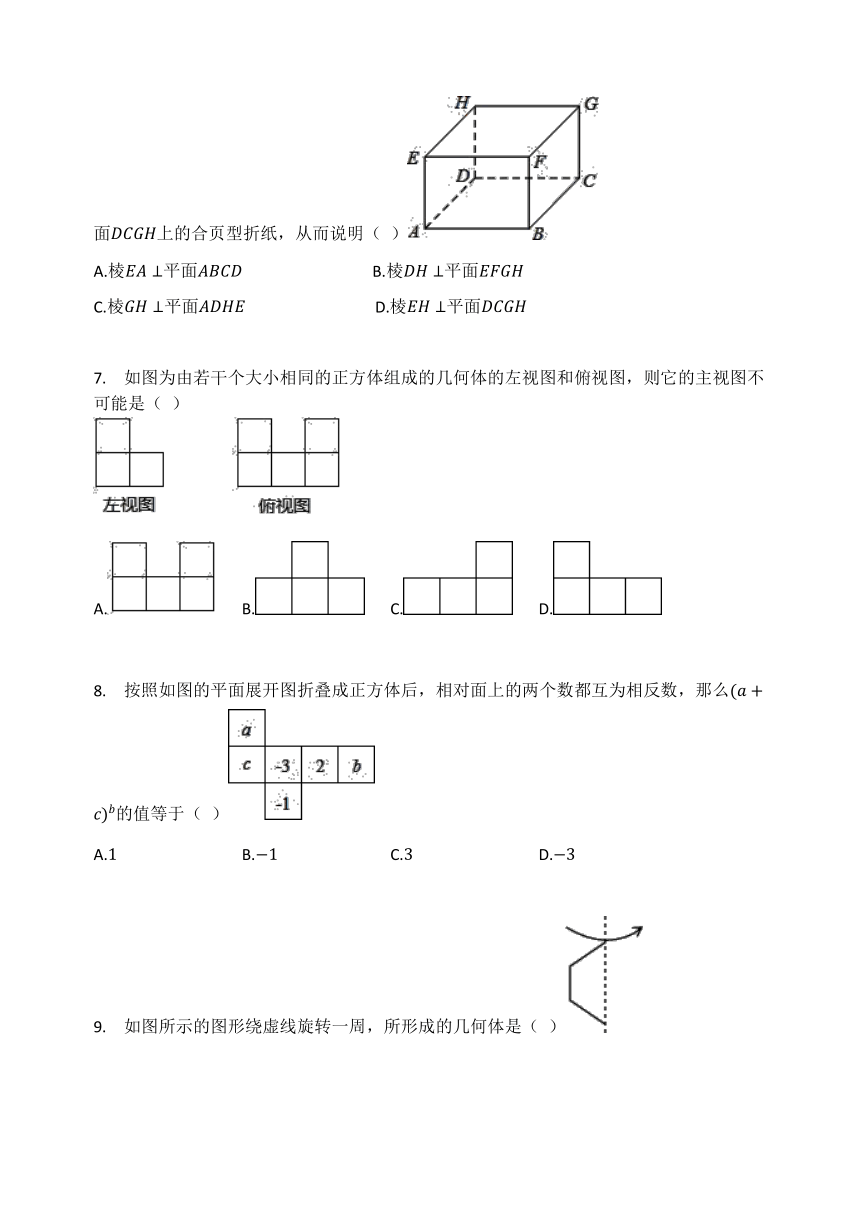
?1. 下列立体图形中,有六个面的是(? ? ? ? )
A.三棱柱 B.圆锥 C.四棱柱 D.圆柱
?
2. 夜里将点燃的蚊香迅速绕一圈,可划出一个曲线,这是因为( )
A.面对成体 B.线动成面 C.点动成线 D.面面相交成线
?
3. 下列平面图形不能够围成正方体的是( )
A. B. C. D.
?
4. 小明用若干个相同的小正方体搭成的一个几何体的三视图如图所示,由此可知,搭成这个几何体的小正方体最多有(? ? ? ? )
A.13个 B.12个 C.11个 D.10个
?
5. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
A.幸 B.福 C.扬 D.州
?6. 如图,在长方体ABCD-EFGH中,可以把面EFGH与面ADHE组成的图形看作直立于面DCGH上的合页型折纸,从而说明( )
A.棱EA⊥平面ABCD B.棱DH⊥平面EFGH
C.棱GH⊥平面ADHE D.棱EH⊥平面DCGH
?
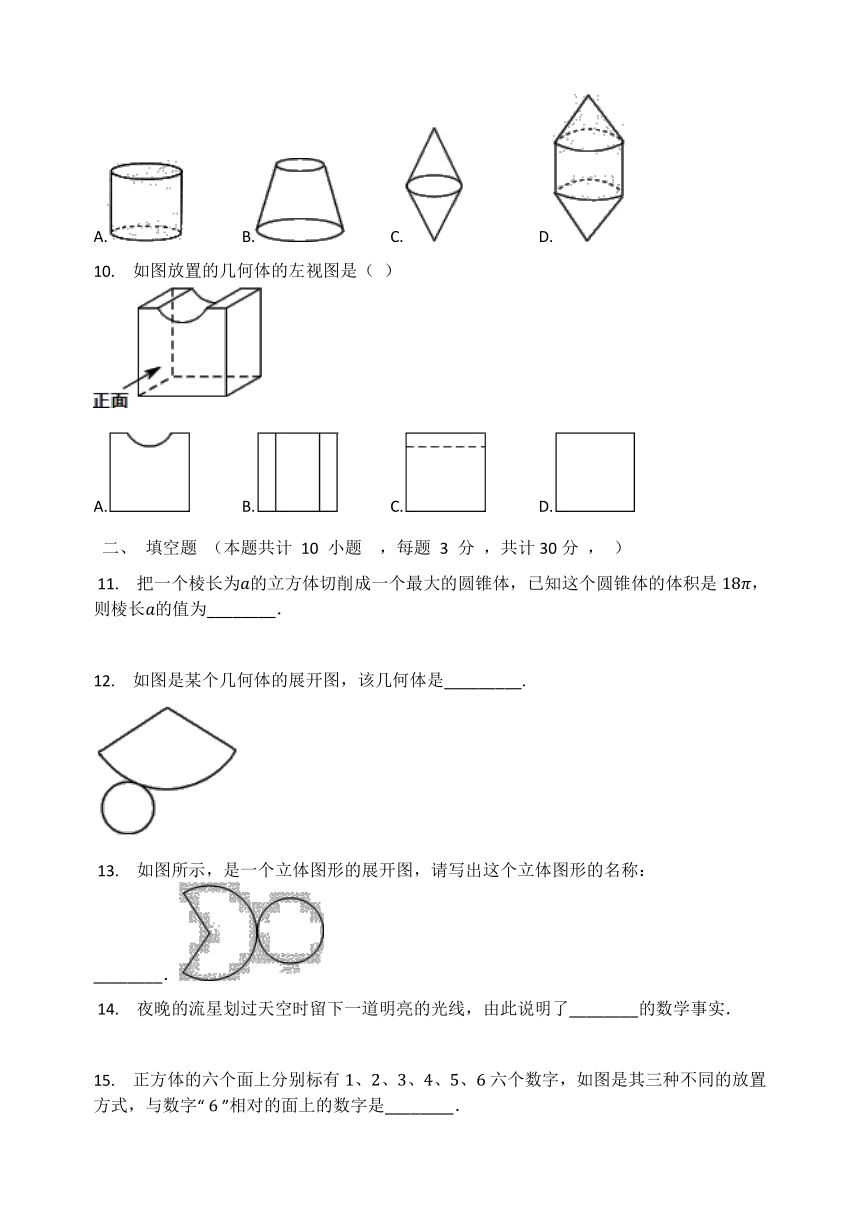
7. 如图为由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( )
A. B. C. D.
?
8. 按照如图的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么(a+c)b的值等于( )
A.1 B.-1 C.3 D.-3
?
9. 如图所示的图形绕虚线旋转一周,所形成的几何体是( )
A. B. C. D.?
10. 如图放置的几何体的左视图是( )
A. B. C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?11. 把一个棱长为a的立方体切削成一个最大的圆锥体,已知这个圆锥体的体积是18π,则棱长a的值为________.
?
12. 如图是某个几何体的展开图,该几何体是_________.
?13. 如图所示,是一个立体图形的展开图,请写出这个立体图形的名称:________.
?14. 夜晚的流星划过天空时留下一道明亮的光线,由此说明了________的数学事实.
?
15. 正方体的六个面上分别标有1、2、3、4、5、6六个数字,如图是其三种不同的放置方式,与数字“?6?”相对的面上的数字是________.
?
16. 用一个平面去截圆锥,截面不可能是三角形.________.
?
17. 一张桌子上重叠摆放了若干枚面值一元的硬币,从三个不同方向看它得到的平面图形如图所示,那么桌上共有________枚硬币.
?
18. 在朱自清的《春》中有描写春雨的语句“像牛毛,像细丝,密密地斜织着”这里把雨滴看成了点,请用数学知识解释这一现象________.
?
19. 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,则根据三视图一共有货物________箱.
?
20. 桌上放着一个长方体和一个圆柱体,说出下面三幅图分别是从哪个方向看到的?
________________________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,直角三角形ABC的两条直角边AB和BC分别长4厘米和3厘米,现在以斜边AC为轴旋转一周.求所形成的立体图形的体积.
?
22. 如图是某几何体的三视图.
(1)说出这个几何体的名称;
(2)画出它的立体图形和表面展开图;
(3)根据有关数据计算几何体的表面积和体积.
?23. 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.
(1)画出两种弥补的设计图;
(2)你还有其他的弥补方法吗?尝试画一画.
?
24. 如图,是一个正方体纸盒展开图,请在三个正方形内分别填适当的数,使得折成正方体后相对面上的两个数是互为相反数,你能做到吗?若能,请直接在小正方形内填入数字,若不能,请说明理由.
?
25. 如图所示,长方形ABCD的长AB为10cm,宽AD为6cm,把长方形ABCD绕AB边所在的直线旋转一周,然后用平面沿AB方向去截所得的几何体,求截面的最大面积.
?
26. 如图(1)是一个正方体,不考虑边长的大小,它的平面展开图为图(2),四边形APQC是切正方体的一个截面.问截面的四条线段AC、CQ、QP、PA以分别在展开图的什么位置上?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A,三棱柱有五个面,故此选项错误;
B,圆锥有一个曲面和一个平面组成,故此选项错误;
C,四棱柱有六个面组成,故此选项正确;
D,圆柱有一个曲面和两个平面组成,故此选项错误.
故选C.
2.
【答案】
C
【解答】
解:夜里将点燃的蚊香迅速绕一圈,可划出一个曲线是因为点动成线,
故选C.
3.
【答案】
B
【解答】
解:根据正方体展开图的特点可判断A,D属于“1,4,1”格式,能围成正方体,
C属于“2,2,2”的格式也能围成正方体,B不能围成正方体.
故选B.
4.
【答案】
A
【解答】
解:综合三视图,我们可以得出,这个几何模型的底层有6个小正方体,第二最多5个小正方形,第三层有2个小正方体,
因此搭成这个几何体模型所用的小正方体的个数最多是6+5+2=13个.
故选A.
5.
【答案】
D
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“设”与“福”是相对面,
“建”与“州”是相对面,
“幸”与“扬”是相对面.
故选D.
6.
【答案】
D
【解答】
解:把面EFGH与面ADHE组成的图形看作直立于面DCGH上的合页型折纸,从而说明棱EH⊥平面DCGH,
故选:D.
7.
【答案】
B
【解答】
由俯视图可得此几何体底面有5个小正方形分为3列2排,根据左视图可得这个几何体的主视图中间1列不可能有2层高.
8.
【答案】
B
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“a”与“-1”是相对面,
“b”与“-3”是相对面,
“c”与“2”是相对面,
∵ 相对面上的两个数都互为相反数,
∴ a=1,b=3,c=-2,
∴ (a+c)b=(1-2)3=-1.
故选B.
9.
【答案】
D
【解答】
解:将梯形绕虚线旋转一周,形成的图形是上面和下面分别是圆锥,中间是一个圆柱的组合体.
故选:D.
10.
【答案】
C
【解答】
左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
6
【解答】
解:∵ 把一个棱长为a的立方体切削成一个最大的圆锥体,已知这个圆锥体的体积是18π,
∴ 圆锥体的高为a,底面的直径为a.
∴ 13π(a2)2×a=18π,解得a=6.
故答案为:6.
12.
【答案】
圆锥
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个几何体是圆锥.
故答案为:圆锥.
13.
【答案】
圆锥
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个立体图形是圆锥.
故填:圆锥.
14.
【答案】
点动成线
【解答】
解:夜晚的流星划过天空时留下一道明亮的光线,由此说明了点动成线.
故答案为:点动成线.
15.
【答案】
5
【解答】
解:由三个图形可看出与3相邻的数字有2,4,5,6,所以与3相对的数字是1,
由第二个图和第三个图可看出与6相邻的数是5.
故答案为:5.
16.
【答案】
错误
【解答】
解:如果用平面取截圆锥,平面过圆锥顶点时得到的截面图形是一个三角形,
故用一个平面去截圆锥,截面不可能是三角形,错误.
故答案为:错误.
17.
【答案】
12
【解答】
解:三摞硬币的个数相加得:5+5+2=12.
∴ 桌上共有12枚硬币.
故答案为:12.
18.
【答案】
点动成线
【解答】
“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
19.
【答案】
8
【解答】
解:根据三视图一共有货物8箱,如图:
.
故答案为:8.
20.
【答案】
从左面,从上面,从正面
【解答】
解:
从左面从上面从正面.
故答案为:从左面,从上面,从正面.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:过B作BD⊥AC,
∵ 直角边AB和BC分别长4厘米和3厘米,
∴ AC=32+42=5(厘米),
斜边上的高为“3×4÷2=6(厘米),
所形成的立体图形的体积:
13×π×2.42×5,
=9.6π(立方厘米).
【解答】
解:过B作BD⊥AC,
∵ 直角边AB和BC分别长4厘米和3厘米,
∴ AC=32+42=5(厘米),
斜边上的高为“3×4÷2=6(厘米),
所形成的立体图形的体积:
13×π×2.42×5,
=9.6π(立方厘米).
22.
【答案】
解:(1)这个几何体为三棱柱.
(2)它的立体图形和表面展开图如图所示;
(3)它的表面积为:2×12×3×4+(3+4+5)×10=132(cm2);
它的体积为:12×3×4×10=60(cm3).
【解答】
解:(1)这个几何体为三棱柱.
(2)它的立体图形和表面展开图如图所示;
(3)它的表面积为:2×12×3×4+(3+4+5)×10=132(cm2);
它的体积为:12×3×4×10=60(cm3).
23.
【答案】
解:(1)如图1所示:
(2)有.
如图2所示:
【解答】
解:(1)如图1所示:
(2)有.
如图2所示:
24.
【答案】
解:根据相反数的定义将-2,-0.5,3分别填到2,0.5,-3的对面:
【解答】
解:根据相反数的定义将-2,-0.5,3分别填到2,0.5,-3的对面:
25.
【答案】
由题可得,把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,
圆柱的底面半径为6cm,高为10cm,
∴ 截面的最大面积为6×2×10=120(cm2).
【解答】
由题可得,把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,
圆柱的底面半径为6cm,高为10cm,
∴ 截面的最大面积为6×2×10=120(cm2).
26.
【答案】
解:(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:A-A,C-C,P在EF边上,Q在GF边上.边AC在ABCD面上,AP在ABFE面上,QC在BCGF面上,PQ在EFGH面上.
(3)将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
【解答】
解:(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:A-A,C-C,P在EF边上,Q在GF边上.边AC在ABCD面上,AP在ABFE面上,QC在BCGF面上,PQ在EFGH面上.
(3)将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
.
(满分120分;时间:120分钟)
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?1. 下列立体图形中,有六个面的是(? ? ? ? )
A.三棱柱 B.圆锥 C.四棱柱 D.圆柱
?
2. 夜里将点燃的蚊香迅速绕一圈,可划出一个曲线,这是因为( )
A.面对成体 B.线动成面 C.点动成线 D.面面相交成线
?
3. 下列平面图形不能够围成正方体的是( )
A. B. C. D.
?
4. 小明用若干个相同的小正方体搭成的一个几何体的三视图如图所示,由此可知,搭成这个几何体的小正方体最多有(? ? ? ? )
A.13个 B.12个 C.11个 D.10个
?
5. 如图是一个正方体的表面展开图,则原正方体中与“建”字所在的面相对的面上标的字是( )
A.幸 B.福 C.扬 D.州
?6. 如图,在长方体ABCD-EFGH中,可以把面EFGH与面ADHE组成的图形看作直立于面DCGH上的合页型折纸,从而说明( )
A.棱EA⊥平面ABCD B.棱DH⊥平面EFGH
C.棱GH⊥平面ADHE D.棱EH⊥平面DCGH
?
7. 如图为由若干个大小相同的正方体组成的几何体的左视图和俯视图,则它的主视图不可能是( )
A. B. C. D.
?
8. 按照如图的平面展开图折叠成正方体后,相对面上的两个数都互为相反数,那么(a+c)b的值等于( )
A.1 B.-1 C.3 D.-3
?
9. 如图所示的图形绕虚线旋转一周,所形成的几何体是( )
A. B. C. D.?
10. 如图放置的几何体的左视图是( )
A. B. C. D.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 , )
?11. 把一个棱长为a的立方体切削成一个最大的圆锥体,已知这个圆锥体的体积是18π,则棱长a的值为________.
?
12. 如图是某个几何体的展开图,该几何体是_________.
?13. 如图所示,是一个立体图形的展开图,请写出这个立体图形的名称:________.
?14. 夜晚的流星划过天空时留下一道明亮的光线,由此说明了________的数学事实.
?
15. 正方体的六个面上分别标有1、2、3、4、5、6六个数字,如图是其三种不同的放置方式,与数字“?6?”相对的面上的数字是________.
?
16. 用一个平面去截圆锥,截面不可能是三角形.________.
?
17. 一张桌子上重叠摆放了若干枚面值一元的硬币,从三个不同方向看它得到的平面图形如图所示,那么桌上共有________枚硬币.
?
18. 在朱自清的《春》中有描写春雨的语句“像牛毛,像细丝,密密地斜织着”这里把雨滴看成了点,请用数学知识解释这一现象________.
?
19. 在一个仓库里堆积着正方体的货箱若干,要搬运这些箱子很困难,可是仓库管理员要落实一下箱子的数量,于是就想出一个办法:将这堆货物的三种视图画了出来,则根据三视图一共有货物________箱.
?
20. 桌上放着一个长方体和一个圆柱体,说出下面三幅图分别是从哪个方向看到的?
________________________.
三、 解答题 (本题共计 6 小题 ,共计60分 , ) ?
21. 如图,直角三角形ABC的两条直角边AB和BC分别长4厘米和3厘米,现在以斜边AC为轴旋转一周.求所形成的立体图形的体积.
?
22. 如图是某几何体的三视图.
(1)说出这个几何体的名称;
(2)画出它的立体图形和表面展开图;
(3)根据有关数据计算几何体的表面积和体积.
?23. 如图,小马虎设计了某个产品的包装盒,由于粗心少设计了其中的一部分,请你帮他补上,使该图形能折成一个密封的正方形盒子.
(1)画出两种弥补的设计图;
(2)你还有其他的弥补方法吗?尝试画一画.
?
24. 如图,是一个正方体纸盒展开图,请在三个正方形内分别填适当的数,使得折成正方体后相对面上的两个数是互为相反数,你能做到吗?若能,请直接在小正方形内填入数字,若不能,请说明理由.
?
25. 如图所示,长方形ABCD的长AB为10cm,宽AD为6cm,把长方形ABCD绕AB边所在的直线旋转一周,然后用平面沿AB方向去截所得的几何体,求截面的最大面积.
?
26. 如图(1)是一个正方体,不考虑边长的大小,它的平面展开图为图(2),四边形APQC是切正方体的一个截面.问截面的四条线段AC、CQ、QP、PA以分别在展开图的什么位置上?
参考答案
一、 选择题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
1.
【答案】
C
【解答】
解:A,三棱柱有五个面,故此选项错误;
B,圆锥有一个曲面和一个平面组成,故此选项错误;
C,四棱柱有六个面组成,故此选项正确;
D,圆柱有一个曲面和两个平面组成,故此选项错误.
故选C.
2.
【答案】
C
【解答】
解:夜里将点燃的蚊香迅速绕一圈,可划出一个曲线是因为点动成线,
故选C.
3.
【答案】
B
【解答】
解:根据正方体展开图的特点可判断A,D属于“1,4,1”格式,能围成正方体,
C属于“2,2,2”的格式也能围成正方体,B不能围成正方体.
故选B.
4.
【答案】
A
【解答】
解:综合三视图,我们可以得出,这个几何模型的底层有6个小正方体,第二最多5个小正方形,第三层有2个小正方体,
因此搭成这个几何体模型所用的小正方体的个数最多是6+5+2=13个.
故选A.
5.
【答案】
D
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“设”与“福”是相对面,
“建”与“州”是相对面,
“幸”与“扬”是相对面.
故选D.
6.
【答案】
D
【解答】
解:把面EFGH与面ADHE组成的图形看作直立于面DCGH上的合页型折纸,从而说明棱EH⊥平面DCGH,
故选:D.
7.
【答案】
B
【解答】
由俯视图可得此几何体底面有5个小正方形分为3列2排,根据左视图可得这个几何体的主视图中间1列不可能有2层高.
8.
【答案】
B
【解答】
解:正方体的表面展开图,相对的面之间一定相隔一个正方形,
“a”与“-1”是相对面,
“b”与“-3”是相对面,
“c”与“2”是相对面,
∵ 相对面上的两个数都互为相反数,
∴ a=1,b=3,c=-2,
∴ (a+c)b=(1-2)3=-1.
故选B.
9.
【答案】
D
【解答】
解:将梯形绕虚线旋转一周,形成的图形是上面和下面分别是圆锥,中间是一个圆柱的组合体.
故选:D.
10.
【答案】
C
【解答】
左视图可得一个正方形,上半部分有条看不到的线,用虚线表示.
二、 填空题 (本题共计 10 小题 ,每题 3 分 ,共计30分 )
11.
【答案】
6
【解答】
解:∵ 把一个棱长为a的立方体切削成一个最大的圆锥体,已知这个圆锥体的体积是18π,
∴ 圆锥体的高为a,底面的直径为a.
∴ 13π(a2)2×a=18π,解得a=6.
故答案为:6.
12.
【答案】
圆锥
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个几何体是圆锥.
故答案为:圆锥.
13.
【答案】
圆锥
【解答】
解:因为圆锥的展开图为一个扇形和一个圆形,故这个立体图形是圆锥.
故填:圆锥.
14.
【答案】
点动成线
【解答】
解:夜晚的流星划过天空时留下一道明亮的光线,由此说明了点动成线.
故答案为:点动成线.
15.
【答案】
5
【解答】
解:由三个图形可看出与3相邻的数字有2,4,5,6,所以与3相对的数字是1,
由第二个图和第三个图可看出与6相邻的数是5.
故答案为:5.
16.
【答案】
错误
【解答】
解:如果用平面取截圆锥,平面过圆锥顶点时得到的截面图形是一个三角形,
故用一个平面去截圆锥,截面不可能是三角形,错误.
故答案为:错误.
17.
【答案】
12
【解答】
解:三摞硬币的个数相加得:5+5+2=12.
∴ 桌上共有12枚硬币.
故答案为:12.
18.
【答案】
点动成线
【解答】
“像牛毛,像细丝,密密地斜织着”的语句,这里把雨看成了线,这说明点动成线.
19.
【答案】
8
【解答】
解:根据三视图一共有货物8箱,如图:
.
故答案为:8.
20.
【答案】
从左面,从上面,从正面
【解答】
解:
从左面从上面从正面.
故答案为:从左面,从上面,从正面.
三、 解答题 (本题共计 6 小题 ,每题 10 分 ,共计60分 )
21.
【答案】
解:过B作BD⊥AC,
∵ 直角边AB和BC分别长4厘米和3厘米,
∴ AC=32+42=5(厘米),
斜边上的高为“3×4÷2=6(厘米),
所形成的立体图形的体积:
13×π×2.42×5,
=9.6π(立方厘米).
【解答】
解:过B作BD⊥AC,
∵ 直角边AB和BC分别长4厘米和3厘米,
∴ AC=32+42=5(厘米),
斜边上的高为“3×4÷2=6(厘米),
所形成的立体图形的体积:
13×π×2.42×5,
=9.6π(立方厘米).
22.
【答案】
解:(1)这个几何体为三棱柱.
(2)它的立体图形和表面展开图如图所示;
(3)它的表面积为:2×12×3×4+(3+4+5)×10=132(cm2);
它的体积为:12×3×4×10=60(cm3).
【解答】
解:(1)这个几何体为三棱柱.
(2)它的立体图形和表面展开图如图所示;
(3)它的表面积为:2×12×3×4+(3+4+5)×10=132(cm2);
它的体积为:12×3×4×10=60(cm3).
23.
【答案】
解:(1)如图1所示:
(2)有.
如图2所示:
【解答】
解:(1)如图1所示:
(2)有.
如图2所示:
24.
【答案】
解:根据相反数的定义将-2,-0.5,3分别填到2,0.5,-3的对面:
【解答】
解:根据相反数的定义将-2,-0.5,3分别填到2,0.5,-3的对面:
25.
【答案】
由题可得,把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,
圆柱的底面半径为6cm,高为10cm,
∴ 截面的最大面积为6×2×10=120(cm2).
【解答】
由题可得,把长方形ABCD绕AB边所在的直线旋转一周,得到的几何体为圆柱,
圆柱的底面半径为6cm,高为10cm,
∴ 截面的最大面积为6×2×10=120(cm2).
26.
【答案】
解:(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:A-A,C-C,P在EF边上,Q在GF边上.边AC在ABCD面上,AP在ABFE面上,QC在BCGF面上,PQ在EFGH面上.
(3)将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
【解答】
解:(1)考虑到展开图上有六个顶点没有标出,可想象将展开图折成立体形,并在顶点上标出对应的符号,见图.
(2)根据四边形所在立体图形上的位置,确定其顶点所在的点和棱,以及四条边所在的平面:
顶点:A-A,C-C,P在EF边上,Q在GF边上.边AC在ABCD面上,AP在ABFE面上,QC在BCGF面上,PQ在EFGH面上.
(3)将上面确定的位置标在展开图上,并在对应平面上连线.需要注意的是,立体图上的A,C点在展开图上有三个,B,D点在展开图上有二个,所以在标点连线时必须注意连线所在的平面,连好线的图形如图.
.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
