北师大版数学八年级上册强化限时练: 第5章《二元一次方程组》实际应用题(二)(Word版 含解析)
文档属性
| 名称 | 北师大版数学八年级上册强化限时练: 第5章《二元一次方程组》实际应用题(二)(Word版 含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 58.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2020-12-15 23:47:35 | ||
图片预览



文档简介
1250950011061700八年级上册强化限时练:
第5章《二元一次方程组》实际应用题(二)
满分:100分 限时60分钟
练习一:每题10分,共50分
1.为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学用33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒;甲,乙两种口罩的数量分别是20个/盒,25个/盒.
(1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教育局的要求?
2.在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,把B型口罩的售价调整为进价的15%,求B型口罩降价的百分率.
3.某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的,试求的值.
4.某公园的门票价格如下表:
购票人数
1﹣50人
51﹣100人
100人以上
每人门票价
13元
11元
9元
实验学校初二(1)、二(2)两个班的学生共104人去公园游玩,其中二(1)班的人数不到50人,二(2)班的人数有50多人,经估算,如果两个班都以班为单位分别购票,则一共应付1240元,如果两班联合起来,作为一个团体购票,则可节省不少钱,你能否求出两个班各有多少名学生?联合起来购票能省多少钱?
5.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号电视机的方案中,为使销售利润最多,你选择哪一种进货方案?
练习二:每题10分,共50分
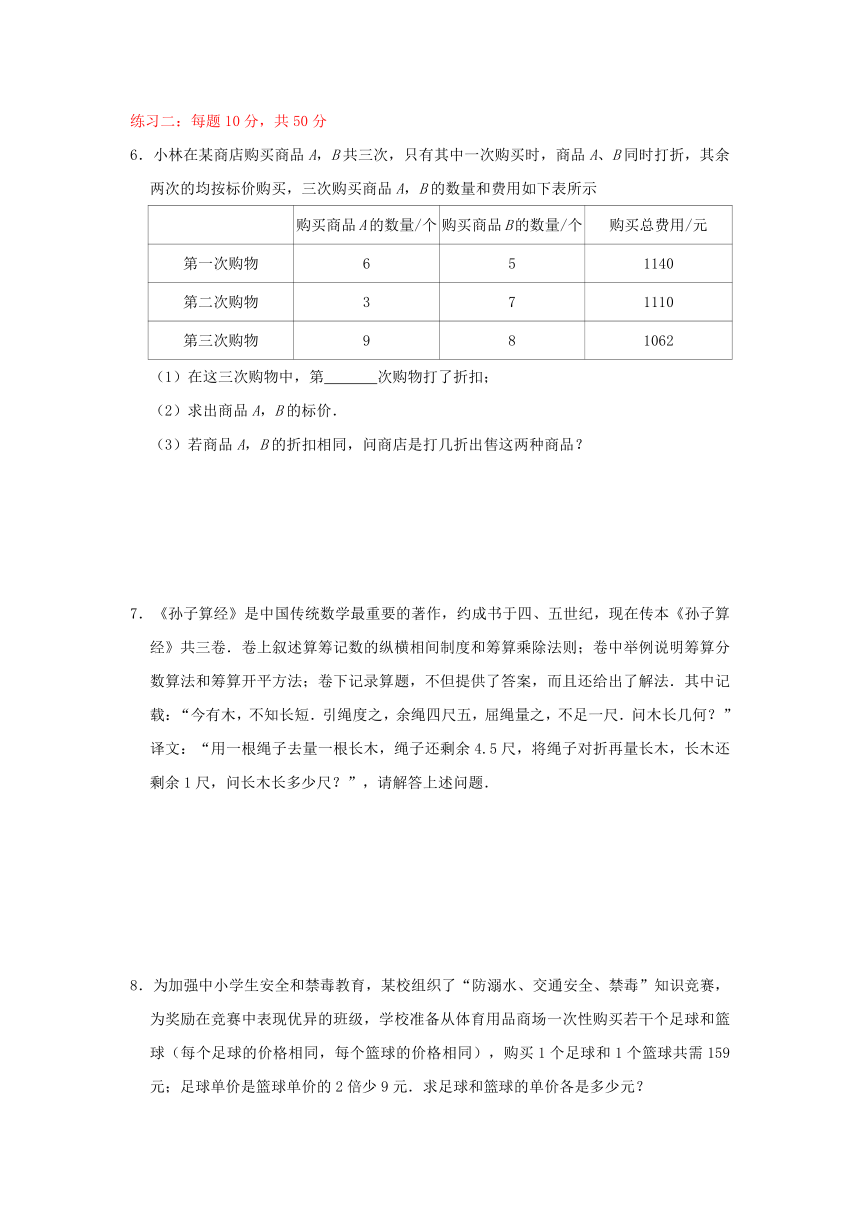
6.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A、B同时打折,其余两次的均按标价购买,三次购买商品A,B的数量和费用如下表所示
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A,B的标价.
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品?
7.《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪,现在传本《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”,请解答上述问题.
8.为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.求足球和篮球的单价各是多少元?
9.某一天,蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子,到菜市场去卖,黄瓜和茄子当天的批发价与零售价如下表所示:
品名
黄瓜
茄子
批发价(元/千克)
3
4
零售价(元/千克)
4
7
当天他卖完这些黄瓜和茄子共赚了90元,这天他批发的黄瓜和茄子分别是多少千克?
10.某物流公司承接A、B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
参考答案
1.解:(1)设新希望中学购进甲种口罩x盒,购进乙种口罩y盒,
依题意,得:,
解得:.
答:新希望中学购进甲种口罩400盒,购进乙种口罩600盒.
(2)购买的口罩总数为:400×20+600×25=23000(个),
全校师生两周需要的用量为:800×2×7×2=22400(个).
∵23000>22400,
∴购买的口罩数量能满足教育局的要求.
2.解:(1)设每只A型口罩的销售利润为x元,每只B型口罩的销售利润为y元,
依题意,得:,
解得:.
答:每只A型口罩的销售利润为0.15元,每只B型口罩的销售利润为0.2元.
(2)设B型口罩降价的百分率为m,
依题意,得(1+100%)(1﹣m)=1×15%,
解得:x=0.925=92.5%.
答:B型口罩降价的百分率为92.5%.
3.解:(1)设小长方形的长和宽分别为x米、y米,
,得,
答:小长方形的长和宽分别为20米、5米;
(2)①,
①+②,得
3(x+y)=a+b,
∴,
∴1个小长方形周长与大长方形周长之比是:,
即1个小长方形周长与大长方形周长之比是1:3;
②∵作品展览区域(阴影部分)面积占展厅面积的,
∴,
∴,
∴(2x+y)(x+2y)=9xy,
化简,得
(x﹣y)2=0,
∴x﹣y=0,
∴x=y,
∴=1.
4.解:设二(1)班有x人,二(2)班有y人
则:
解得:
节省钱数为1240﹣104×9=304元.
答:两个班各有48人和56人,学生联合起来购票能省304元.
5.解:(1)解分三种情况计算:
①设购甲种电视机x台,乙种电视机y台.
解得.
②设购甲种电视机x台,丙种电视机z台.
则,
解得:.
③设购乙种电视机y台,丙种电视机z台.
则
解得:(不合题意,舍去);
(2)方案一:25×150+25×200=8750.
方案二:35×150+15×250=9000元.
答:购甲种电视机25台,乙种电视机25台;或购甲种电视机35台,丙种电视机15台.
购买甲种电视机35台,丙种电视机15台获利最多.
6.解:(1)观察表格中的数据,可知:第三次购物,购进的数量更多,总价更低,
∴第三次购物打了折扣.
故答案为:三.
(2)设商品A的标价为x元,商品B的标价为y元,
依题意,得:,
解得:.
答:商品A的标价为90元,商品B的标价为120元.
(3)设商店是打m折出售这两种商品,
依题意,得:(90×9+120×8)×=1062,
解得:m=6.
答:商店是打6折出售这两种商品.
7.解:设绳子长x尺,长木长y尺,
依题意,得:,
解得:.
答:长木长6.5尺.
8.解:设足球的单价为x元/个、篮球的单价为y元/个,
根据题意得:,
解得:.
答:足球的单价为103元/个,篮球的单价为56元/个.
9.解:设批发的黄瓜是x千克,茄子是y千克,由题意得
解得
答:这天他批发的黄瓜15千克,茄子是25千克.
10.解:(1)设A种货物运输了x吨,设B种货物运输了y吨,
依题意得:,
解之得:.
答:物流公司月运输A种货物100吨,B种货物150吨.
(2)设A种货物为a吨,则B种货物为(330﹣a)吨,
依题意得:a≤(330﹣a)×2,
解得:a≤220,
设获得的利润为W元,则W=70a+40(330﹣a)=30a+13200,
根据一次函数的性质,可知W随着a的增大而增大
当W取最大值时a=220,
即W=19800元.
所以该物流公司7月份最多将收到19800元运输费.
第5章《二元一次方程组》实际应用题(二)
满分:100分 限时60分钟
练习一:每题10分,共50分
1.为了抗击新冠病毒,保护学生和教师的生命安全,新希望中学用33000元购进甲、乙两种医用口罩共计1000盒,甲,乙两种口罩的售价分别是30元/盒,35元/盒;甲,乙两种口罩的数量分别是20个/盒,25个/盒.
(1)求新希望中学甲、乙两种口罩各购进了多少盒?
(2)按照教育局要求,学校必须储备两周的用量,新希望中学师生共计800人,每人每天2个口罩,问购买的口罩数量是否能满足教育局的要求?
2.在近期“抗疫”期间,某药店销售A、B两种型号的口罩,已知销售800只A型和450只B型的利润为210元,销售400只A型和600只B型的利润为180元.
(1)求每只A型口罩和B型口罩的销售利润;
(2)在销售时,该药店开始时将B型口罩提价100%,当收回成本后,为了让利给消费者,把B型口罩的售价调整为进价的15%,求B型口罩降价的百分率.
3.某校举办“迎亚运“学生书画展览,现要在长方形展厅中划出3个形状、大小完全一样的小长方形(图中阴影部分)区域摆放作品.
(1)如图1,若大长方形的长和宽分别为45米和30米,求小长方形的长和宽.
(2)如图2,若大长方形的长和宽分别为a和b
①直接写出1个小长方形周长与大长方形周长之比;
②若作品展览区域(阴影部分)面积占展厅面积的,试求的值.
4.某公园的门票价格如下表:
购票人数
1﹣50人
51﹣100人
100人以上
每人门票价
13元
11元
9元
实验学校初二(1)、二(2)两个班的学生共104人去公园游玩,其中二(1)班的人数不到50人,二(2)班的人数有50多人,经估算,如果两个班都以班为单位分别购票,则一共应付1240元,如果两班联合起来,作为一个团体购票,则可节省不少钱,你能否求出两个班各有多少名学生?联合起来购票能省多少钱?
5.某商场计划拨款9万元从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号电视机共50台,用去9万元,请你研究一下商场的进货方案;
(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号电视机的方案中,为使销售利润最多,你选择哪一种进货方案?
练习二:每题10分,共50分
6.小林在某商店购买商品A,B共三次,只有其中一次购买时,商品A、B同时打折,其余两次的均按标价购买,三次购买商品A,B的数量和费用如下表所示
购买商品A的数量/个
购买商品B的数量/个
购买总费用/元
第一次购物
6
5
1140
第二次购物
3
7
1110
第三次购物
9
8
1062
(1)在这三次购物中,第 次购物打了折扣;
(2)求出商品A,B的标价.
(3)若商品A,B的折扣相同,问商店是打几折出售这两种商品?
7.《孙子算经》是中国传统数学最重要的著作,约成书于四、五世纪,现在传本《孙子算经》共三卷.卷上叙述算筹记数的纵横相间制度和筹算乘除法则;卷中举例说明筹算分数算法和筹算开平方法;卷下记录算题,不但提供了答案,而且还给出了解法.其中记载:“今有木,不知长短.引绳度之,余绳四尺五,屈绳量之,不足一尺.问木长几何?”
译文:“用一根绳子去量一根长木,绳子还剩余4.5尺,将绳子对折再量长木,长木还剩余1尺,问长木长多少尺?”,请解答上述问题.
8.为加强中小学生安全和禁毒教育,某校组织了“防溺水、交通安全、禁毒”知识竞赛,为奖励在竞赛中表现优异的班级,学校准备从体育用品商场一次性购买若干个足球和篮球(每个足球的价格相同,每个篮球的价格相同),购买1个足球和1个篮球共需159元;足球单价是篮球单价的2倍少9元.求足球和篮球的单价各是多少元?
9.某一天,蔬菜经营户老李用了145元从蔬菜批发市场批发一些黄瓜和茄子,到菜市场去卖,黄瓜和茄子当天的批发价与零售价如下表所示:
品名
黄瓜
茄子
批发价(元/千克)
3
4
零售价(元/千克)
4
7
当天他卖完这些黄瓜和茄子共赚了90元,这天他批发的黄瓜和茄子分别是多少千克?
10.某物流公司承接A、B两种货物运输业务,已知5月份A货物运费单价为50元/吨,B货物运费单价为30元/吨,共收取运费9500元;6月份由于油价上涨,运费单价上涨为:A货物70元/吨,B货物40元/吨;该物流公司6月承接的A种货物和B种数量与5月份相同,6月份共收取运费13000元.
(1)该物流公司5月份运输两种货物各多少吨?
(2)该物流公司预计7月份运输这两种货物330吨,且A货物的数量不大于B货物的2倍,在运费单价与6月份相同的情况下,该物流公司7月份最多将收到多少运输费?
参考答案
1.解:(1)设新希望中学购进甲种口罩x盒,购进乙种口罩y盒,
依题意,得:,
解得:.
答:新希望中学购进甲种口罩400盒,购进乙种口罩600盒.
(2)购买的口罩总数为:400×20+600×25=23000(个),
全校师生两周需要的用量为:800×2×7×2=22400(个).
∵23000>22400,
∴购买的口罩数量能满足教育局的要求.
2.解:(1)设每只A型口罩的销售利润为x元,每只B型口罩的销售利润为y元,
依题意,得:,
解得:.
答:每只A型口罩的销售利润为0.15元,每只B型口罩的销售利润为0.2元.
(2)设B型口罩降价的百分率为m,
依题意,得(1+100%)(1﹣m)=1×15%,
解得:x=0.925=92.5%.
答:B型口罩降价的百分率为92.5%.
3.解:(1)设小长方形的长和宽分别为x米、y米,
,得,
答:小长方形的长和宽分别为20米、5米;
(2)①,
①+②,得
3(x+y)=a+b,
∴,
∴1个小长方形周长与大长方形周长之比是:,
即1个小长方形周长与大长方形周长之比是1:3;
②∵作品展览区域(阴影部分)面积占展厅面积的,
∴,
∴,
∴(2x+y)(x+2y)=9xy,
化简,得
(x﹣y)2=0,
∴x﹣y=0,
∴x=y,
∴=1.
4.解:设二(1)班有x人,二(2)班有y人
则:
解得:
节省钱数为1240﹣104×9=304元.
答:两个班各有48人和56人,学生联合起来购票能省304元.
5.解:(1)解分三种情况计算:
①设购甲种电视机x台,乙种电视机y台.
解得.
②设购甲种电视机x台,丙种电视机z台.
则,
解得:.
③设购乙种电视机y台,丙种电视机z台.
则
解得:(不合题意,舍去);
(2)方案一:25×150+25×200=8750.
方案二:35×150+15×250=9000元.
答:购甲种电视机25台,乙种电视机25台;或购甲种电视机35台,丙种电视机15台.
购买甲种电视机35台,丙种电视机15台获利最多.
6.解:(1)观察表格中的数据,可知:第三次购物,购进的数量更多,总价更低,
∴第三次购物打了折扣.
故答案为:三.
(2)设商品A的标价为x元,商品B的标价为y元,
依题意,得:,
解得:.
答:商品A的标价为90元,商品B的标价为120元.
(3)设商店是打m折出售这两种商品,
依题意,得:(90×9+120×8)×=1062,
解得:m=6.
答:商店是打6折出售这两种商品.
7.解:设绳子长x尺,长木长y尺,
依题意,得:,
解得:.
答:长木长6.5尺.
8.解:设足球的单价为x元/个、篮球的单价为y元/个,
根据题意得:,
解得:.
答:足球的单价为103元/个,篮球的单价为56元/个.
9.解:设批发的黄瓜是x千克,茄子是y千克,由题意得
解得
答:这天他批发的黄瓜15千克,茄子是25千克.
10.解:(1)设A种货物运输了x吨,设B种货物运输了y吨,
依题意得:,
解之得:.
答:物流公司月运输A种货物100吨,B种货物150吨.
(2)设A种货物为a吨,则B种货物为(330﹣a)吨,
依题意得:a≤(330﹣a)×2,
解得:a≤220,
设获得的利润为W元,则W=70a+40(330﹣a)=30a+13200,
根据一次函数的性质,可知W随着a的增大而增大
当W取最大值时a=220,
即W=19800元.
所以该物流公司7月份最多将收到19800元运输费.
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
