江苏省高邮市2011-2012学年度第一学期期中调研高二数学试题
文档属性
| 名称 | 江苏省高邮市2011-2012学年度第一学期期中调研高二数学试题 |
|
|
| 格式 | zip | ||
| 文件大小 | 173.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2011-11-12 00:00:00 | ||
图片预览


文档简介
高邮市2011—2012学年度第一学期期中调研试题
高 二 数 学
(满分160分 考试时间120分钟)
注意事项:
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.
2.第一部分试题答案均写在答题卷相应位置,答在其它地方无效.
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上)
空间直角坐标系中,点A(-3,4,0)与点B(2,-1,5)的距离是 ★ .
直线的倾斜角是 ★ .
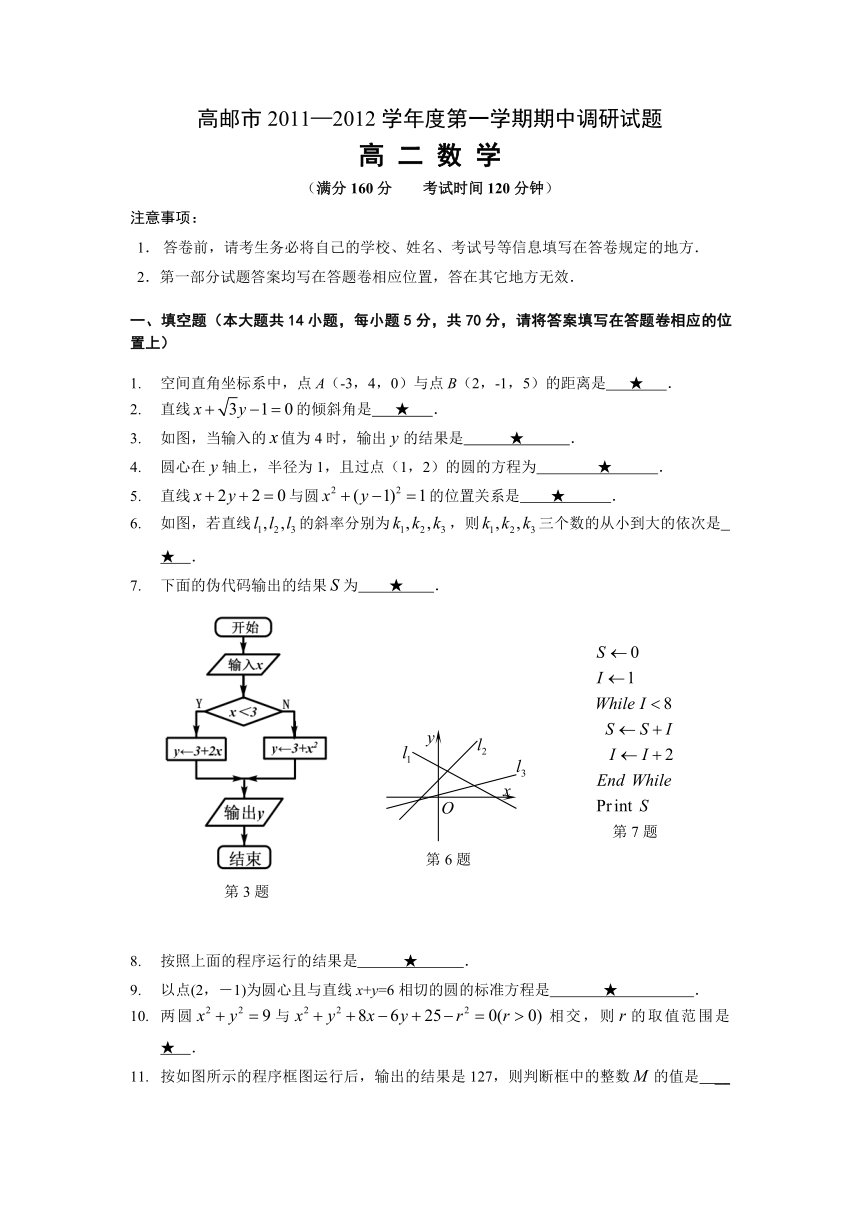
如图,当输入的值为4时,输出的结果是 ★ .
圆心在轴上,半径为1,且过点(1,2)的圆的方程为 ★ .
直线与圆的位置关系是 ★ .
如图,若直线的斜率分别为,则三个数的从小到大的依次是 ★ .
下面的伪代码输出的结果为 ★ .
按照上面的程序运行的结果是 ★ .
以点(2,-1)为圆心且与直线x+y=6相切的圆的标准方程是 ★ .
两圆与相交,则的取值范围是 ★ .
按如图所示的程序框图运行后,输出的结果是127,则判断框中的整数的值是 __★_ .
观察程序,程序在运行结束后循环语句执行了 ★ 次.
已知点关于直线的对称点为,则圆关于直线对称的圆的方程为 ★ .
过圆内一点的最短弦长为,且到直线的距离为1,则点的坐标是 ★ .
二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本题满分14分)
已知直线,.
(Ⅰ)若直线,求实数的值;
(Ⅱ)是否存在实数,使得直线与垂直?若存在,求出的值;若不存在,说明理由.
16.(本题满分14分)
已知直线
(Ⅰ)求过两直线交点且与直线平行的直线方程;
(Ⅱ)直线过两直线交点且与正半轴交于A、B两点,△ABO的面积为4,求直线的方程.
17.(本题满分15分)
设顶点坐标,圆为的外接圆.
(Ⅰ)求圆的标准方程
(Ⅱ)直线过点(1,3)且与圆M相交于P、Q,弦PQ长为,求直线的方程.
18.(本题满分15分)
设直线l1:y=k1x+1,l2:y=k2x-1,其中实数k1,k2满足k1k2+1=0.
(Ⅰ)证明:直线l1与l2相交;
(Ⅱ)证明:直线l1与l2的交点在圆x2+y2=1上.
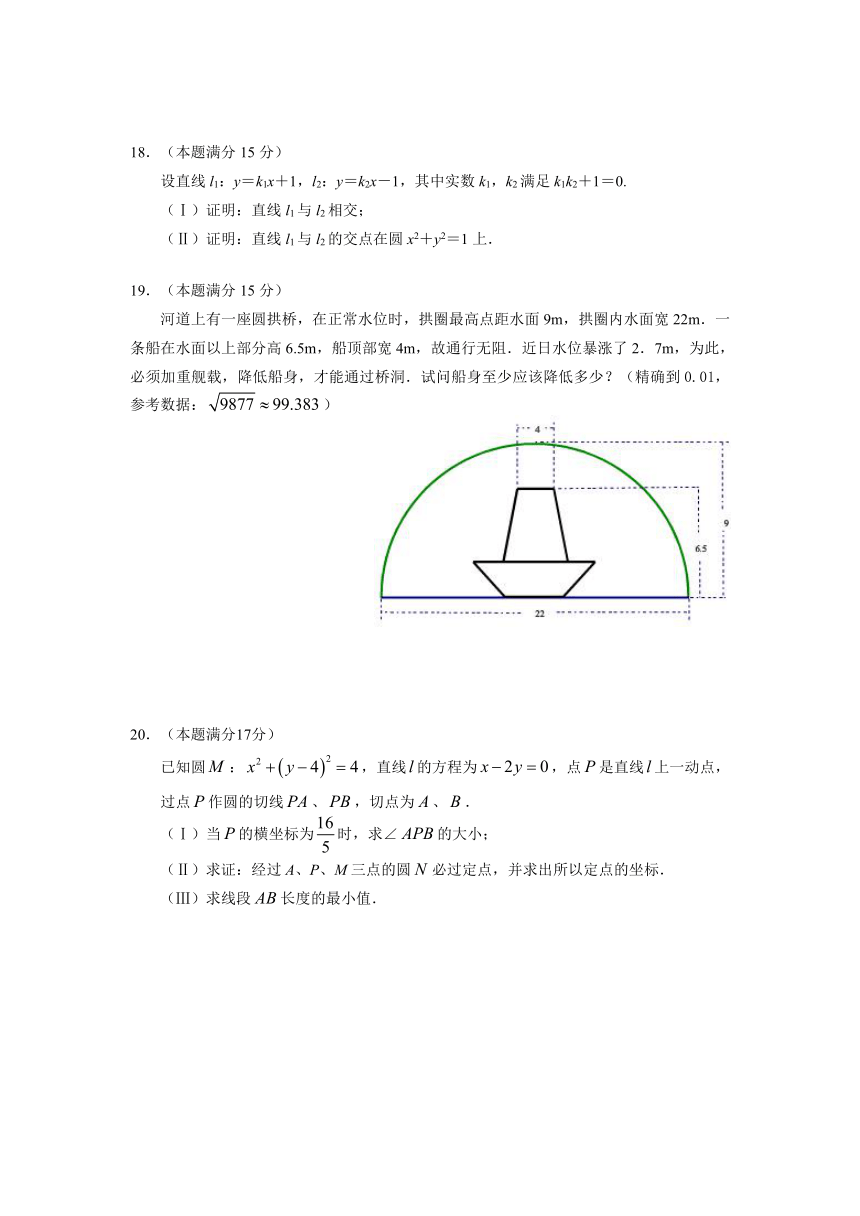
19.(本题满分15分)
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:)
20.(本题满分17分)
已知圆:,直线的方程为,点是直线上一动点,过点作圆的切线、,切点为、.
(Ⅰ)当的横坐标为时,求∠的大小;
(Ⅱ)求证:经过A、P、M三点的圆必过定点,并求出所以定点的坐标.
(Ⅲ)求线段长度的最小值.
2011~2012学年第一学期高邮市高二数学期中试卷(参考答案)
1. 2. 3.19 4. 5.相离 6.
7. 16 8.5. 9.(x-2)2+(y+1)2= 10. 11. 6 12.15
13. 14.
15.解:(Ⅰ)因为直线,所以,解得或 ……2分
若,则,即,此时重合,不合题意; ………5分
若,则,即,此时;
综上所述,. ………8分
(Ⅱ)若在这样的实数,即,………11分
因△=9-16<0,方程无解,所以不存在这样的,使得直线与垂直.14分
16.解:(Ⅰ)由,得,所以的交点为(2,1) ……3分
又所求直线与平行,所以所求直线的斜率为, ……5分
所求直线方程为即 ……7分
(Ⅱ)方法一:由题可知,直线的斜率存在,且.
则直线的方程为
令,得>0
令,得>0
所以,解得 ……13分
所以的方程为 ……14分
方法二:由题可知,直线的横、纵截距a、b存在,且a>0、b>0,则:
又过点(2,1),△ABO的面积为4
所以, ……10分
解得, ……13分
所以方程为即. ……14分
17. 解:(Ⅰ)设圆M的方程为
因圆M过点,所以, ……4分
解得,所以圆M的方程为即. 7分
(Ⅱ)若直线与x轴垂直,则:,
由,得,所以EF=,符合题意. ……9分
若直线与x轴不垂直,设即
点M(0,-1)到的距离
EF=, ……12分
解得,此时方程为
综上所述,直线的方程是或. ……15分
18. 解:(Ⅰ)反证法:假设l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+1=0,得k+2=1.
此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交. ……6分
(Ⅱ)方法一:由方程组
解得交点P的坐标(x,y)为 ……10分
而x2+y2=2+2
===1.
此即表明交点P(x,y)在圆x2+y2=1上. ……15分
方法二:交点P的坐标(x,y)满足
故知x≠0,从而 ……10分
代入k1k2+1=0,得·+1=0.
整理后,得x2+y2=1,
所以交点P在圆x2+y2=1上. ……15分
19.解:以正常水位时河道中央O为原点,过点O垂直于水面的直线为y轴,建立平面直角坐标系,如图所示。 ……………………3分
设桥拱圆的圆心,半径为r,则圆的方程为
依题意得:
解得:,
∴圆的方程为……………………6分
当时, ……………………9分
……………………13分
∴为使船能通过桥洞,应至少降低船身0.38m …………………15分
20.解:(Ⅰ)由题可知,圆M的半径r=2,,
因为PA是圆M的一条切线,所以∠MAP=90°
又因MP==2r,
又∠MPA=30°,∠APB=60°; ……4分
(Ⅱ)设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆以MP为直径,其方程为: 即
由, ……7分
解得或,所以圆过定点 ……9分
(Ⅲ)因圆方程为即
……①
圆:即 ……②
②-①得圆方程与圆相交弦所在直线方程为…11分
点M到直线的距离 ……13分
相交弦长即 ……15分
当时,AB有最小值 ……17分
第7题
第3题
第6题
第11题
S0
I1
While S<120
SS+I
I I+1
End While
第12题
Print
第8题
高 二 数 学
(满分160分 考试时间120分钟)
注意事项:
答卷前,请考生务必将自己的学校、姓名、考试号等信息填写在答卷规定的地方.
2.第一部分试题答案均写在答题卷相应位置,答在其它地方无效.
一、填空题(本大题共14小题,每小题5分,共70分,请将答案填写在答题卷相应的位置上)
空间直角坐标系中,点A(-3,4,0)与点B(2,-1,5)的距离是 ★ .
直线的倾斜角是 ★ .
如图,当输入的值为4时,输出的结果是 ★ .
圆心在轴上,半径为1,且过点(1,2)的圆的方程为 ★ .
直线与圆的位置关系是 ★ .
如图,若直线的斜率分别为,则三个数的从小到大的依次是 ★ .
下面的伪代码输出的结果为 ★ .
按照上面的程序运行的结果是 ★ .
以点(2,-1)为圆心且与直线x+y=6相切的圆的标准方程是 ★ .
两圆与相交,则的取值范围是 ★ .
按如图所示的程序框图运行后,输出的结果是127,则判断框中的整数的值是 __★_ .
观察程序,程序在运行结束后循环语句执行了 ★ 次.
已知点关于直线的对称点为,则圆关于直线对称的圆的方程为 ★ .
过圆内一点的最短弦长为,且到直线的距离为1,则点的坐标是 ★ .
二、解答题:(本大题共6道题,计90分.解答应写出必要的文字说明、证明过程或演算步骤)
15.(本题满分14分)
已知直线,.
(Ⅰ)若直线,求实数的值;
(Ⅱ)是否存在实数,使得直线与垂直?若存在,求出的值;若不存在,说明理由.
16.(本题满分14分)
已知直线
(Ⅰ)求过两直线交点且与直线平行的直线方程;
(Ⅱ)直线过两直线交点且与正半轴交于A、B两点,△ABO的面积为4,求直线的方程.
17.(本题满分15分)
设顶点坐标,圆为的外接圆.
(Ⅰ)求圆的标准方程
(Ⅱ)直线过点(1,3)且与圆M相交于P、Q,弦PQ长为,求直线的方程.
18.(本题满分15分)
设直线l1:y=k1x+1,l2:y=k2x-1,其中实数k1,k2满足k1k2+1=0.
(Ⅰ)证明:直线l1与l2相交;
(Ⅱ)证明:直线l1与l2的交点在圆x2+y2=1上.
19.(本题满分15分)
河道上有一座圆拱桥,在正常水位时,拱圈最高点距水面9m,拱圈内水面宽22m.一条船在水面以上部分高6.5m,船顶部宽4m,故通行无阻.近日水位暴涨了2.7m,为此,必须加重舰载,降低船身,才能通过桥洞.试问船身至少应该降低多少?(精确到0.01,参考数据:)
20.(本题满分17分)
已知圆:,直线的方程为,点是直线上一动点,过点作圆的切线、,切点为、.
(Ⅰ)当的横坐标为时,求∠的大小;
(Ⅱ)求证:经过A、P、M三点的圆必过定点,并求出所以定点的坐标.
(Ⅲ)求线段长度的最小值.
2011~2012学年第一学期高邮市高二数学期中试卷(参考答案)
1. 2. 3.19 4. 5.相离 6.
7. 16 8.5. 9.(x-2)2+(y+1)2= 10. 11. 6 12.15
13. 14.
15.解:(Ⅰ)因为直线,所以,解得或 ……2分
若,则,即,此时重合,不合题意; ………5分
若,则,即,此时;
综上所述,. ………8分
(Ⅱ)若在这样的实数,即,………11分
因△=9-16<0,方程无解,所以不存在这样的,使得直线与垂直.14分
16.解:(Ⅰ)由,得,所以的交点为(2,1) ……3分
又所求直线与平行,所以所求直线的斜率为, ……5分
所求直线方程为即 ……7分
(Ⅱ)方法一:由题可知,直线的斜率存在,且.
则直线的方程为
令,得>0
令,得>0
所以,解得 ……13分
所以的方程为 ……14分
方法二:由题可知,直线的横、纵截距a、b存在,且a>0、b>0,则:
又过点(2,1),△ABO的面积为4
所以, ……10分
解得, ……13分
所以方程为即. ……14分
17. 解:(Ⅰ)设圆M的方程为
因圆M过点,所以, ……4分
解得,所以圆M的方程为即. 7分
(Ⅱ)若直线与x轴垂直,则:,
由,得,所以EF=,符合题意. ……9分
若直线与x轴不垂直,设即
点M(0,-1)到的距离
EF=, ……12分
解得,此时方程为
综上所述,直线的方程是或. ……15分
18. 解:(Ⅰ)反证法:假设l1与l2不相交,则l1与l2平行,有k1=k2,代入k1k2+1=0,得k+2=1.
此与k1为实数的事实相矛盾,从而k1≠k2,即l1与l2相交. ……6分
(Ⅱ)方法一:由方程组
解得交点P的坐标(x,y)为 ……10分
而x2+y2=2+2
===1.
此即表明交点P(x,y)在圆x2+y2=1上. ……15分
方法二:交点P的坐标(x,y)满足
故知x≠0,从而 ……10分
代入k1k2+1=0,得·+1=0.
整理后,得x2+y2=1,
所以交点P在圆x2+y2=1上. ……15分
19.解:以正常水位时河道中央O为原点,过点O垂直于水面的直线为y轴,建立平面直角坐标系,如图所示。 ……………………3分
设桥拱圆的圆心,半径为r,则圆的方程为
依题意得:
解得:,
∴圆的方程为……………………6分
当时, ……………………9分
……………………13分
∴为使船能通过桥洞,应至少降低船身0.38m …………………15分
20.解:(Ⅰ)由题可知,圆M的半径r=2,,
因为PA是圆M的一条切线,所以∠MAP=90°
又因MP==2r,
又∠MPA=30°,∠APB=60°; ……4分
(Ⅱ)设P(2b,b),因为∠MAP=90°,所以经过A、P、M三点的圆以MP为直径,其方程为: 即
由, ……7分
解得或,所以圆过定点 ……9分
(Ⅲ)因圆方程为即
……①
圆:即 ……②
②-①得圆方程与圆相交弦所在直线方程为…11分
点M到直线的距离 ……13分
相交弦长即 ……15分
当时,AB有最小值 ……17分
第7题
第3题
第6题
第11题
S0
I1
While S<120
SS+I
I I+1
End While
第12题
第8题
同课章节目录
